


Números quadrados perfeitos cujas raízes quadradas são múltiplos do número 3 apresentam outras regularidades numéricas: a soma dos seus algarismos têm como resultados números múltiplos de 3 e 9.
Pelo critério da divisibilidade por 3, a soma dos algarismos de um número tem que ser um número divisível por 3.
Pelo critério da divisibilidade por 9, a soma dos algarismos de um número tem que ser um número divisível por 9.
Podemos também encontrar números divisíveis por 3 ou por 9:
a) somando os algarismos que compõem determinado número e posteriormente subtraindo a soma desses algarismos com esse número ou;
b) somando os algarismos que compõem determinado número e posteriomente somando esse número com a soma dos seus algarismos.
No estudo que se segue, veremos que números quadrados perfeitos cujas raízes quadradas são múltiplos de 3, apresentam uma relação direta da soma dos seus algarismos com os números 3 e 9.
Quadrado 9
9 : 3 = 3 (9 é divisível por 3)
9 : 9 = 1 (9 é divisível por 9)
Observação: 9 dividido por 9 tem como quociente o número 1.
(1 é um quadrado perfeito)
A soma dos quocientes 1 + 3 = 4
(4 é um quadrado perfeito)
Quadrado 36 - a soma dos algarismos: 3 + 6 = 9
A raiz quadrada de 36 é 6 (6 é múltiplo de 3)
36 : 3 = 12 (36 é divisível por 3)
36 : 9 = 4 (36 é divisível por 9)
Observação: 36 dividido por 9 tem como quociente o número 4
(4 é um quadrado perfeito)
A soma dos quocientes 12 + 4 = 16
(16 é um quadrado perfeito).
Quadrado 81 - a soma dos algarismos: 8 + 1 = 9
A raiz quadrada de 81 é 9 (9 é múltiplo de 3)
81 : 3 = 27 (81 é divisível por 3)
81 : 9 = 9 (81 é divisível por 9)
Observação: 81 dividido por 9 tem como quociente o número 9
(9 é um quadrado perfeito)
A soma dos quocientes 27 + 9 = 36
(36 é um quadrado perfeito)
Quadrado 144 - a soma dos algarismos: 1 + 4 + 4 = 9
A raiz quadrada de 144 é 12 (12 é múltiplo de 3)
144 : 3 = 48 (144 é divisível por 3)
144 : 9 = 16 (144 é divisível por 9)
Observação: 144 dividido por 9 tem como quociente o número 16
(16 é um quadrado perfeito)
A soma dos quocientes 48 + 16 = 64
(64 é um quadrado perfeito)
Quadrado 225 - a soma dos algarismos: 2 + 2 + 5 = 9
A raiz quadrada de 225 é 15 (15 é múltiplo de 3)
225 : 3 = 75 (225 é divisível por 3)
225 : 9 = 25 (225 é divisível por 9)
Observação: 225 dividido por 9 tem como quociente o número 25
(25 é um quadrado perfeito)
A soma dos quocientes 75 + 25 = 100
(100 é um quadrado perfeito)
Quadrado 324 - a soma dos algarismos: 3 + 2 + 4 = 9
A raiz quadrada de 324 é 18 (18 é múltiplo de 3)
324 : 3 = 108 (324 é divisível por 3)
324 : 9 = 36 (324 é divisível por 9)
Observação: 324 dividido por 9 tem como quociente o número 36
(36 é um quadrado perfeito)
A soma dos quocientes 108 + 36 = 144
(144 é um quadrado perfeito)
Quadrado 441 - a soma dos algarismos: 4 + 4 + 1 = 9
A raiz quadrada de 441 é 21 (21 é múltiplo de 3)
441 : 3 = 147 (441 é divisível por 3)
441 : 9 = 49 (441 é divisível por 9)
Observação: 441 dividido por 9 tem como quociente o número 49
(49 é um quadrado perfeito)
A soma dos quocientes 147 + 49 = 196
(196 é um quadrado perfeito)
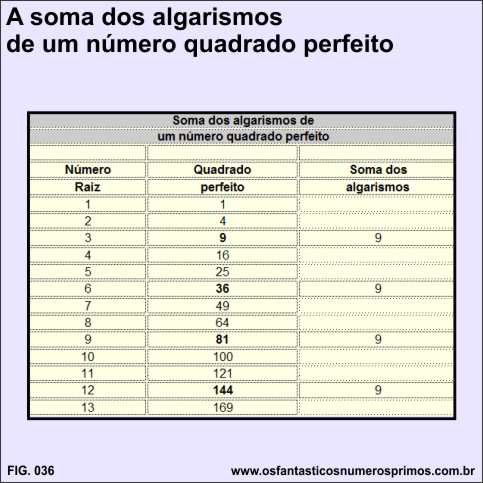
A seguinte tabela apresenta os 97 primeiros números quadrados perfeitos e suas respectivas raízes quadradas.
| Soma dos algarismos de | ||
|---|---|---|
| um número quadrado perfeito | ||
| Número | Quadrado | Soma dos |
| Raiz | perfeito | algarismos |
| 1 | 1 | |
| 2 | 4 | |
| 3 | 9 | 9 |
| 4 | 16 | |
| 5 | 25 | |
| 6 | 36 | 9 |
| 7 | 49 | |
| 8 | 64 | |
| 9 | 81 | 9 |
| 10 | 100 | |
| 11 | 121 | |
| 12 | 144 | 9 |
| 13 | 169 | |
| 14 | 196 | |
| 15 | 225 | 9 |
| 16 | 256 | |
| 17 | 289 | |
| 18 | 324 | 9 |
| 19 | 361 | |
| 20 | 400 | |
| 21 | 441 | 9 |
| 22 | 484 | |
| 23 | 529 | |
| 24 | 576 | 18 |
| 25 | 625 | |
| 26 | 676 | |
| 27 | 729 | 18 |
| 28 | 784 | |
| 29 | 841 | |
| 30 | 900 | 9 |
| 31 | 961 | |
| 32 | 1.024 | |
| 33 | 1.089 | 18 |
| 34 | 1.156 | |
| 35 | 1.225 | |
| 36 | 1.296 | 18 |
| 37 | 1.369 | |
| 38 | 1.444 | |
| 39 | 1.521 | 9 |
| 40 | 1.600 | |
| 41 | 1.681 | |
| 42 | 1.764 | 18 |
| 43 | 1.849 | |
| 44 | 1.936 | |
| 45 | 2.025 | 9 |
| 46 | 2.116 | |
| 47 | 2.209 | |
| 48 | 2.304 | 9 |
| 49 | 2.401 | |
| 50 | 2.500 | |
| 51 | 2.601 | 9 |
| 52 | 2.704 | |
| 53 | 2.809 | |
| 54 | 2.916 | 18 |
| 55 | 3.025 | |
| 56 | 3.136 | |
| 57 | 3.249 | 18 |
| 58 | 3.364 | |
| 59 | 3.481 | |
| 60 | 3.600 | 9 |
| 61 | 3.721 | |
| 62 | 3.844 | |
| 63 | 3.969 | 27 |
| 64 | 4.096 | |
| 65 | 4.225 | |
| 66 | 4.356 | 18 |
| 67 | 4.489 | |
| 68 | 4.624 | |
| 69 | 4.761 | 18 |
| 70 | 4.900 | |
| 71 | 5.041 | |
| 72 | 5.184 | 18 |
| 73 | 5.329 | |
| 74 | 5.476 | |
| 75 | 5.625 | 18 |
| 76 | 5.776 | |
| 77 | 5.929 | |
| 78 | 6.084 | 18 |
| 79 | 6.241 | |
| 80 | 6.400 | |
| 81 | 6.561 | 18 |
| 82 | 6.724 | |
| 83 | 6.889 | |
| 84 | 7.056 | 18 |
| 85 | 7.225 | |
| 86 | 7.396 | |
| 87 | 7.569 | 27 |
| 88 | 7.744 | |
| 89 | 7.921 | |
| 90 | 8.100 | 9 |
| 91 | 8.281 | |
| 92 | 8.464 | |
| 93 | 8.649 | 27 |
| 94 | 8.836 | |
| 95 | 9.025 | |
| 96 | 9.216 | 18 |
| 97 | 9.409 | |
| www.osfantasticosnumerosprimos.com.br | ||
Autor: Ricardo Silva
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
032-a-soma-dos-algarismos-de-um-numero-parte-1
033-a-soma-dos-algarismos-de-um-numero-primo-parte 1
035-a-soma-dos-algarismos-de-um-numero-parte 3
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato