


Octógono é um polígono regular formado por 8 lados com a mesma medida e também por 8 ângulos internos com a mesma medida.
Este estudo tem como base a figura geométrica do octógono e as sequências numéricas originárias a partir de sua forma.
Desenhando-se vários octógonos equidistantes e numerando os seus vértices em sentido horário a partir do octógono central, obtêm-se várias sequências numéricas que veremos a seguir.
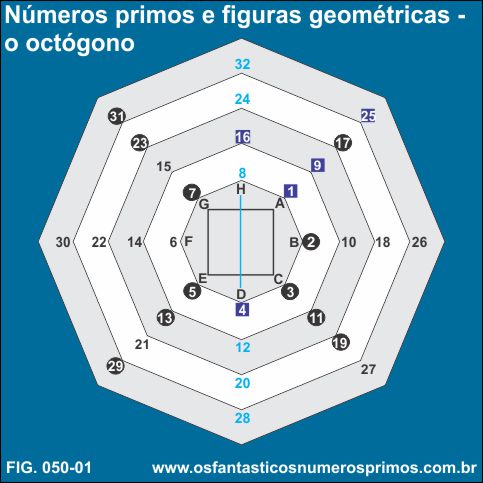
Por ser um polígono com 8 lados, cada sequência que parte de cada vértice são formadas só com sequências de números ímpares e sequências só com pares.
A disposição dos números se apresenta da seguinte forma: 4 vértices com números pares e 4 vértices com números ímpares. No vértice B, há somente um único número primo par, o número 2.
Nos vértices A, C, E e G, concentra-se os demais números primos, distribuídos em forma de um "XIS" ou uma cruz enclinada a 45º.
Unindo-se os vértices A, C, E e G, formamos a figura de um quadrado. Há três duplas de vértices: (A e G), (B e F) e (C e E), cujas somas em cada octógono têm como resultados números múltiplo de 8 que se encontram no vértice H.
Partindo-se de cada vértice do octógono central têm-se oito principais sequências numéricas do octógono.
A diferença entre um número posterior e anterior de cada vértice é de 8 unidades.
1) Vértice A tem-se a seguinte sequência de números ímpares: 1, 9, 17, 25, 33, ..., entre eles, números primos.
9 - 1 = 8
2) Vértice B tem-se a seguinte sequência de números pares: 2, 10, 18, 26, 34, ...
10 - 2 = 8
3) Vértice C tem-se a seguinte sequência de números ímpares: 3, 11, 19, 27, 35, ..., entre eles, números primos.
11 - 3 = 8
4) Vértice D tem-se a seguinte sequência de múltiplo de 4: 4, 12, 20, 28, 36, ..., originários de 4 multiplicados por fatores ímpares: (4x1=4), (4x3=12), etc.
12 - 4 = 8
5) Vértice E tem-se a seguinte sequência de números ímpares: 5, 13, 21, 29, 37, ..., entre eles, números primos.
13 - 5 = 8
6) Vértice F tem-se a seguinte sequência de números pares: 6, 14, 22, 30, 38, ...
14 - 6 = 8
7) Vértice G, tem-se a seguinte sequência números ímpares: 7, 15, 23, 31, 39, ..., entre eles, números primos.
17 - 7 = 7
8) Vértice H tem-se a seguinte sequência dos múltiplos de 8: 8, 16, 24, 32, 40, ...
16 - 8 = 8
| Octógono e sequências numéricas | ||||||||
|---|---|---|---|---|---|---|---|---|
| Ordem dos | Vértices | |||||||
| Octógonos | A | B | C | D | E | F | G | H |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 3 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 4 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| 5 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 6 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| 7 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
| 8 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 |
| 9 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 |
| 10 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 11 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 |
| 12 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 |
| 13 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 |
| 14 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 |
| 15 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| 16 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 |
| 17 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 |
| 18 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 |
| 19 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 |
| 20 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 |
| 21 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 |
| 22 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 |
| 23 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 |
| 24 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 |
| 25 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 26 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 |
| 27 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 |
| 28 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 |
| 29 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 |
| 30 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 |
| 31 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 |
| 32 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 |
| 33 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 |
| 34 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 |
| 35 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 |
| 36 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 |
| 37 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 |
| 38 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 |
| 39 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 |
| 40 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 |
| 41 | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 |
| 42 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 |
| 43 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 |
| 44 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 |
| 45 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 |
| 46 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 |
| 47 | 369 | 370 | 371 | 372 | 373 | 374 | 375 | 376 |
| 48 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 |
| 49 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 |
| 50 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| www.osfantasticosnumerosprimos.com.br | ||||||||
Somando-se números dos vértices A e B, temos como resultados números ímpares que se encontram no vértice C de octógono de ordem ímpar.
1) A soma dos vértices A e B do primeiro octógono.
1 + 2 = 3
O 3 está no vértice C do primeiro octógono
2) A soma dos vértices A e B do segundo octógono.
9 + 10 = 19
O 19 está no vértice C do terceiro octógono
3) A soma dos vértices A e B do terceiro octógono.
17 + 18 = 35
O 35 está no vértice C do quinto octógono
Somando-se números dos vértices B e C, temos como resultados números ímpares que se encontram no vértice E de octógono de ordem ímpar.
1) A soma dos vértices B e C do primeiro octógono.
2 + 3 = 5
O 5 está no vértice D do primeiro octógono
2) A soma dos vértices B e C do segundo octógono.
10 + 11 = 21
O 21 está no vértice E do terceiro octógono
3) A soma dos vértices B e C do terceiro octógono.
18 + 19 = 37
O 37 está no vértice E do quinto octógono
Somando-se números dos vértices C e D, temos como resultados números ímpares que se encontram no vértice G de octógono de ordem ímpar.
1) A soma dos vértices C e D do primeiro octógono.
3 + 4 = 7
O 7 está no vértice G do primeiro octógono
2) A soma dos vértices C e D do segundo octógono.
11 + 12 = 23
O 23 está no vértice G do terceiro octógono
3) A soma dos vértices C e D do terceiro octógono.
19 + 20 = 39
O 39 está no vértice G do quinto octógono
Somando-se números dos vértices D e E, temos como resultados números ímpares que se encontram no vértice A de octógono de ordem par.
1) A soma dos vértices D e E do primeiro octógono.
4 + 5 = 9
O 9 está no vértice A do segundo octógono
2) A soma dos vértices D e E do segundo octógono.
12 + 13 = 25
O 25 está no vértice A do quarto octógono
3) A soma dos vértices D e E do terceiro octógono.
20 + 21 = 41
O 41 está no vértice A do sexto octógono
Somando-se números dos vértices E e F, temos como resultados números ímpares que se encontram no vértice C de octógono de ordem par.
1) A soma dos vértices E e F do primeiro octógono.
5 + 6 = 11
O 11 está no vértice C do segundo octógono
2) A soma dos vértices E e F do segundo octógono.
13 + 14 = 27
O 27 está no vértice C do quarto octógono
3) A soma dos vértices E e F do terceiro octógono.
21 + 22 = 43
O 43 está no vértice C do sexto octógono
Somando-se números dos vértices F e G, temos como resultados números ímpares que se encontram no vértice E de octógono de ordem par.
1) A soma dos vértices F e G do primeiro octógono.
6 + 7 = 13
O 13 está no vértice E do segundo octógono
2) A soma dos vértices F e G do segundo octógono.
14 + 15 = 29
O 29 está no vértice E do quarto octógono
3) A soma dos vértices F e G do terceiro octógono.
22 + 23 = 45
O 45 está no vértice E do sexto octógono
Somando-se números dos vértices G e H, temos como resultados números ímpares que se encontram no vértice G de octógono de ordem par.
1) A soma dos vértices G e H do primeiro octógono.
7 + 8 = 15
O 15 está no vértice G do segundo octógono
2) A soma dos vértices G e G do segundo octógono.
15 + 16 = 31
O 31 está no vértice G do quarto octógono
3) A soma dos vértices G e H do terceiro octógono.
23 + 24 = 47
O 47 está no vértice G do sexto octógono
1) O vértice B é a média aritmética dos vértices A e C.
| Ordem dos | Vértices | Soma Vértices |
Média Aritmética |
|
| Octógonos | A | C | A e C | Vértice B |
| 1 | 1 | 3 | 4 | 2 |
| 2 | 9 | 11 | 20 | 10 |
| 3 | 17 | 19 | 36 | 18 |
| 4 | 25 | 27 | 52 | 26 |
| 5 | 33 | 35 | 68 | 34 |
2) O vértice C é a média aritmética dos vértices B e D.
| Ordem dos | Vértices | Soma Vértices |
Média Aritmética |
|
| Octógonos | B | D | B e D | Vértice B |
| 1 | 2 | 4 | 6 | 3 |
| 2 | 10 | 12 | 22 | 11 |
| 3 | 18 | 20 | 38 | 19 |
| 4 | 26 | 28 | 54 | 27 |
| 5 | 34 | 36 | 70 | 35 |
3) O vértice D é a média aritmética dos vértices C e E.
| Ordem dos | Vértices | Soma Vértices |
Média Aritmética |
|
| Octógonos | C | E | C e E | Vértice D |
| 1 | 3 | 5 | 8 | 4 |
| 2 | 11 | 13 | 24 | 12 |
| 3 | 19 | 21 | 40 | 20 |
| 4 | 27 | 29 | 56 | 28 |
| 5 | 35 | 37 | 72 | 36 |
4) O vértice E é a média aritmética dos vértices D e F.
| Ordem | Vértices | Soma Vértices |
Média Aritmética |
|
| Octógono | D | F | D e F | Vértice E |
| 1 | 4 | 6 | 10 | 5 |
| 2 | 12 | 14 | 26 | 13 |
| 3 | 20 | 22 | 42 | 21 |
| 4 | 28 | 30 | 58 | 29 |
| 5 | 36 | 38 | 74 | 37 |
5) O vértice F é a média aritmética dos vértices E e G.
| Ordem dos | Vértices | Soma Vértices |
Média Aritmética |
|
| Octógonos | E | G | E e G | Vértice F |
| 1 | 5 | 7 | 12 | 6 |
| 2 | 13 | 15 | 28 | 14 |
| 3 | 21 | 23 | 44 | 22 |
| 4 | 29 | 31 | 60 | 30 |
| 5 | 37 | 39 | 76 | 38 |
6) O vértice G é a média aritmética dos vértices F e H.
| Ordem dos | Vértices | Soma Vértices |
Média Aritmética |
|
| Octógonos | F | H | F e H | Vértice G |
| 1 | 6 | 8 | 14 | 7 |
| 2 | 14 | 16 | 30 | 15 |
| 3 | 22 | 24 | 46 | 23 |
| 4 | 30 | 32 | 62 | 31 |
| 5 | 38 | 40 | 78 | 39 |
No vértice A, há a ocorrência de termos da sequência dos números octogonais centrados intercalados entre seus termos:
1, 9, 25, 49, 81, 121, 169, 225, 289... (células amarela na tabela acima).
O intervalo entre um termo e outro a partir do termo 8, na tabela acima, ocorre a sequência dos números naturais.
entre 9 e 25 - 1 intervalo
entre 25 e 49 - 2 intervalos
entre 49 e 81 - 3 intervalos
e assim sucessivamente...
Interessante observar que nos números figurados octogonais centrados há ocorrências de números quadrados perfeitos ímpares: 1, 9, 25, 49, 81, 121, 19, 225, 289,...
Os números figurados octagonais centrados também podem ser obtidos da diferença entre os termos da sequência dos números figurados decagonais.
Faça o downlod da Tabela de Números Figurados (Números Poligonais).
Outra propriedade que podemos extrair do diagrama de quadrados equistantes com vértices numerados é a Aritmética do Relógio, também denominada de Aritmética Modular, Aritmética Módulo M, conceitos estes desenvolvidos pelos matemáticos Leonhard Euler e Carl Friedrich Gauss.
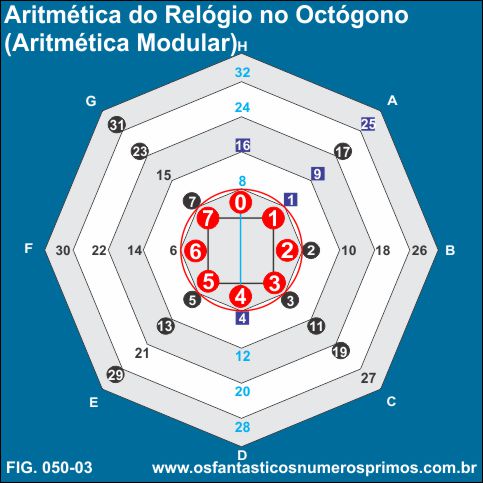
No vértice H, como se observa, tende a se concentrar a sequência de múltiplos de 8, isto é, números que quando divididos por 8, deixam resto 0 (zero).
Nos vértices A, B, C, D, E, F e G podemos dizer que tem algo de "especial", são números que quando divididos por 8 deixam restos 1, 2, 3, 4, 5, 6, 7 respectivamente.
Este fato de sobrar restos em divisões entre números inteiros fez surgir o conceito de congruência / equivalência entre números.
Partindo-se do "marcador 0" e girando em sentido horário tantos vértices que se queira, ao pararmos em determinado número e dividirmos esse número por 6, os possíveis restos podem ser: 0, 1, 2, 3, 4, 5, 6 ou 7.
Dái podemos dizer:
1) um número é congruente / equivalente a outro número, no nosso exemplo (módulo 8), porque quando dividido por 8 podem deixar os seguintes restos: 0, 1, 2, 3, 4, 5, 6 ou 7;
a ≡ b (módulo m)
a e b ao serem divididos por m deixam restos iguais.
o sinal (≡), com 3 traços simboliza congruência.
Exemplo:
9 ≡ 17 (módulo 8)
9 e 17 deixam resto 1 quando divididos por 8.
9 : 8 = 1 e resto 1
17 : 8 = 2 e resto 1
2) ou também a e b serão congruentes módulo m quando b-a for divisível por m;
Exemplo:
9 ≡ 17 (módulo 8)
porque
17 - 9 = 8
8 é divisível por 8
A Aritmética Modular / Aritmética Módulo M / Aritmética do Relógio é um ramo da Teoria dos Números e têm diversas aplicações, entre elas, a Criptografia.
Autor: Ricardo Silva
atualizado em maio/2025
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato