


Desenhando-se vários triângulos equidistantes e distribuindo os números da Sequência de Fibonacci nos seus vértices em sentido horário a partir do triângulo central, obtêm-se 3 sequências numéricas com características numéricas distintas as quais são apresentadas a seguir.
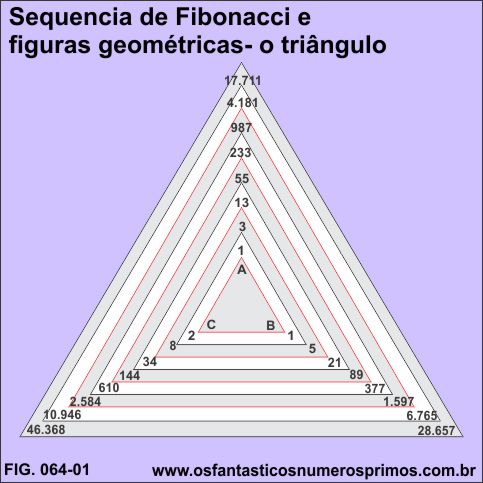
Na distribuição dos números, o vértice C concentra-se a sequência de números pares, nos vértices A e B números ímpares.
Neste estudo, veremos como os números de Fibonacci se interrelacionam com a própria sequência de Fibonacci.
A soma de dois números do vértice A correspondem ao dobro de um número do vértice C.
Exemplo a)
1 + 3 = 4
(4 é o dobro de 2)
Exemplo b)
3 + 13 = 16
(16 é o dobro de 8)
Exemplo c)
13 + 55 = 68
(68 é o dobro de 34)
A soma de dois números do vértice B correspondem ao dobro de um número do vértice A.
Exemplo a)
1 + 5 = 6
(6 é o dobro de 3)
Exemplo b)
5 + 21 = 26
(26 é o dobro de 13)
Exemplo c)
21 + 89 = 110
(110 é o dobro de 55)
A soma de dois números do vértice C correspondem ao dobro de um número do vértice B.
Exemplo a)
2 + 8 = 10
(10 é o dobro de 5)
Exemplo b)
8 + 34 = 42
(42 é o dobro de 21)
Exemplo c)
34 + 144 = 178
(178 é o dobro de 89)
1) A soma dos quadrados de dois números consecutivos do vértice A corresponde ao dobro de um número do vértice B.
Exemplo a)
1² + 3² =
= 1 + 9 = 10
10 é o dobro de 5
(O 5 está no segundo triângulo do vértice B)
Exemplo b)
3² + 13² =
= 9 + 169 = 178
178 é o dobro de 89
(O 89 está no quarto triângulo do vértice B)
2) A soma dos quadrados de dois números consecutivos do vértice B corresponde ao dobro de um número do vértice A.
Exemplo a)
1² + 5² =
= 1 + 25 = 26
26 é o dobro de 13
(O 13 está no terceiro triângulo do vértice A)
Exemplo b)
5² + 21² =
= 25 + 441 = 466
466 é o dobro de 89
(O 89 está no quinto triângulo do vértice A)
3) A soma dos quadrados de dois números consecutivos do vértice C, corresponde ao dobro de um número do vértice C
Exemplo a)
2² + 8² =
=4 + 64=68
68 é o dobro de 34
(O 34 está no terceiro triângulo do vértice C)
Exemplo b)
8² + 34² =
=64 + 1156 = 1220
1220 é o dobro de 620
(O 620 está no quinto triângulo do vértice C)
Autor: Ricardo Silva
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato