Página de estudos de matemática e sequências numéricas

Tabuada de números triangulares - 066

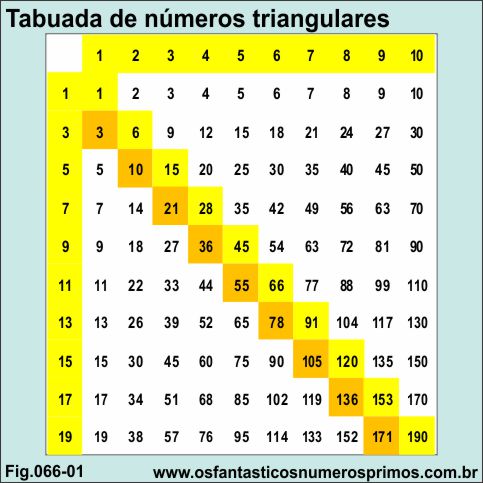
Montando-se uma variação de tabuada em que na primeira linha há a sequência de números naturais e na primeira coluna a sequência de números ímpares, os produtos obtidos na diagonal principal e adjacente são números triangulares.

Números triangulares

Números triangulares, também chamados de números figurados, são aqueles que podem ser representados com figuras de triângulos atravês de pontos arranjados.

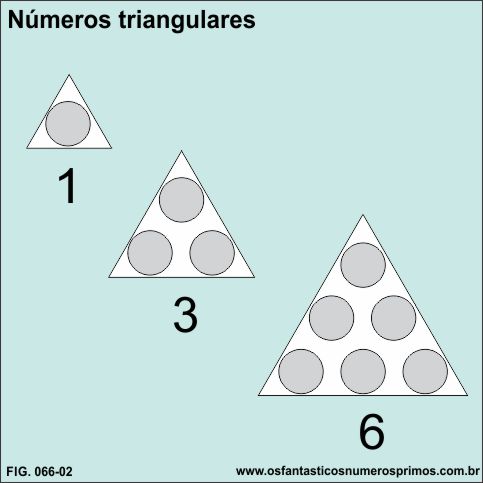
Triângulo de 1 ponto,

- o número 1 é um número triangular.

Triângulo de 3 pontos,

- 3 é um numero triangular.

Triângulo de 6 pontos,

- 6 é um numero triangular.

Formação de números triangulares

Podemos também obter um número triangular através da soma de números naturais consecutivos a partir de 1.

1 + 2 = 3

1 + 2 + 3 = 6

1 + 2 + 3 + 4 = 10

1 + 2 + 3 + 4 + 5 = 15

Método de obtenção de números triangulares

Outro método de se obter números triangulares é atráves de tabuada construída de forma que na primeira linha horizontal tenha a sequência de números naturais: 1, 2, 3, 4, 5, 7, 8, 9, 10,.... e uma coluna com números ímpares: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19,...

Múltiplicando-se um número ímpar da primeira coluna com um número da primeira linha ou vice-versa, obtem-se o produto entre eles.

Diagonal principal (amarela)

Nas multiplicações entre os números, forma-se na diagonal principal sequência de números triangulares de posições ímpares (veja a tabela acima).

Interessante notar que a coluna dos números ímpares da Tabuada de Números Triangulares também determina a ordem / posição dos números triangulares:

Exemplos

a) 1 x 1 = 1

1 é primeiro número triangular

b) 3 x 2 = 6

6 é o terceiro número triangular

c) 5 x 3 = 15

15 é o quinto número triangular

Diagonal adjacente (laranja)

Exemplos:

a) 3 x 1 = 3

3 é segundo número triangular

b) 5 x 2 = 10

(10 é o quarto número triangular

c) 7 x 3 = 21

21 é o sexto número triangular

Números quadrados perfeitos ímpares

A soma de dois números triangulares consecutivos tem como resultado um número quadrado perfeito.

Na Tabuada de Números Triangulares, somando-se um número da diagonal principal e outro da diagonal adjacente que se encontram na mesma linha, obtem-se um número quadrado perfeito ímpar.

Exemplos:

a) 3 + 6 = 9

interessante observar que 3 e 6 são múltiplos de 3.

b) 10 + 15 = 25

interessante observar que 10 e 15 são múltiplos de 5.

c) 21 + 28 = 49

interessante observar que 21 e 28 são múltiplos de 7.

Na Tabuada de Números Triangulares, somando-se um número da diagonal principal e outro da diagonal adjacente que se encontram na mesma coluna, obtem-se um número quadrado perfeito par.

Exemplos:

a) 1 + 3 = 4

interessante observar que 3 não é múltiplo e nem divisor de 4.

b) 6 + 10 = 16

interessante observar que 6 e 10 não são múltiplos e nem divisores de 16.

b) 15 + 21 = 36

interessante observar que 15 e 21 não são múltiplos e nem divisores de 36.

Tabela de números triangulares de posições ímpares

Podemos também construir uma tabela conforme modelo abaixo de forma que multiplicando um número natural por um número ímpar / posição, obtem-se um número triangular de posição ímpar.

Veja que o número ímpar equivale a posição de um número triangular.

Propriedade da tabela de números triangulares

A Tabela de números triangulares de posições ímpares apresenta interessantes propriedades numéricas:

Escolhendo qualquer número e subtraindo 1 unidade do seu dobro, a diferença é o segundo fator para se obter um número triangular de posição ímpar.

Exemplos:

a) 2 x 3 = 6

O segundo fator 3 é a diferença de 4 (dobro de 2) menos 1 unidade.

b) 3 x 5 = 15

O segundo fator 5 é a diferença de 6 (dobro de 3) menos 1 unidade.

c) 4 x 7 = 28

O segundo fator 7 é a diferença de 8 (dobro de 4) menos 1 unidade.

Escolhendo qualquer número e mutiplicando-o pelo seu dobro e posteriormente subtraindo esse número, o resultado será um número triangular.

Exemplos:

a) Número escolhido: 2

O dobro: 4

O produto de 2 x 4 = 8

O fator 2 subtraído do produto 8 tem como resultado o triangular 6.

8 - 2 = 6

b) Número escolhido: 3

O dobro: 6

O produto de 3 x 6 = 18

O fator 3 subtraído do produto 18 tem como resultado o triangular 15.

18 - 3 = 15

Exemplo c)

Número escolhido: 4

O dobro: 8

O produto de 4 x 8 = 32

O fator 4 subtraído do produto 32 tem como resultado o triangular 28.

32 - 4 = 28

O segundo fator subtraído de um número triangular de posição ímpar tem como resultado um número triangular antecessor.

Exemplos:

a) 2 x 3 = 6

O segundo fator: 3

6 - 3 = 3

3 é o número triangular antecessor do triangular 6.

b) 3 x 5 = 15

O segundo fator: 5

15 - 5 = 10

10 é o número triangular antecessor do triangular 15.

c) 4 x 7 = 28

O segundo fator: 7

28 - 7 = 21

21 é o número triangular antecessor do triangular 28.

No livro digital Números Triangulares e Sequências Numéricas são apresentados vários estudos e métodos de como se obter números triangulares semelhante ao Triângulo de Pascal.

Progressão Aritmética (P.A) Finita e último termo quadrado ímpar

Outra propriedade que a Tabuada de Números Triangulares revela é que Progressão Aritmética Finita em que:

a) o primeiro terno é uma raiz quadrada ímpar;

b) a razão (diferença entre dois termos) é uma raiz quadrada;

c) o último termo é o quadrado do primeiro termo.

a média aritmética entre o primeiro e último termo é um número triangular e que somado com o termo antecessor tem como resultado o último termo da P.A. Finita

Exemplo 1)

P.A. (3, 6, 9)

Média aritmética

( 3 + 9 ) / 2 = 6

6 é um número triangular

3 é o termo antecessor de 6 na P.A

A soma de 2 números triangulares é um quadrado perfeito

3 + 6 = 9

Exemplo 2)

P.A. (5, 10, 15, 20, 25)

Média aritmética

( 5 + 25) / 2 = 15

15 é um número triangular

10 é o termo antecessor de 15 na P.A

A soma de 2 números triangulares é um quadrado perfeito

10 + 15 = 25

Progressão Aritmética (P.A) Finita e último termo quadrado par

Progressões aritméticas artiméticas em que

a) o primeiro terno é uma raiz quadrada par;

b) a razão (diferença entre dois termos) é uma raiz quadrada;

c) o último termo é o quadrado do primeiro termo.

os números triângulares não aparecem em pares, isto é, não estão evidentes na P.A.

Exemplo 1)

P.A ( 4, 8, 12, 16 )

Na P.A. não aparece par de números triangulares.

Para se saber os 2 triagulares cuja soma é 16, procedemos assim:

i)

( 16 - 4 ) / 2 = 6

ii)

( 16 + 4 ) / 2 = 10

A soma de 6 + 10 = 16

Exemplo 2)

P.A ( 6, 12, 18, 24, 30, 36 )

Na P.A. não aparece par de números triangulares.

Para se saber os 2 triagulares cuja soma é 16, procedemos assim:

i)

( 36 - 6 ) / 2 = 15

ii)

( 36 + 6 ) / 2 = 21

A soma de 15 + 21 = 36

Fórmulas para se obterem números triangulares

Fórmulas a partir de números quadrados e suas respectivas raízes quadradas.

A metade da diferença entre um número quadrado perfeito e a sua raiz é um número triangular, para n >1.

A metade da soma entre um número quadrado perfeito e a sua raiz é um número triangular, para n >1.

Fórmula a partir de números consecutivos.

Autor: Ricardo Silva

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-126-tabuada-propriedade-subtracao

011-estudos-127-tabuada-e-numeros-triangulares

011-estudos-147-tabuada-e-ternos-pitagoricos

Livro digital (e-book)

Tabuada de Pythagoras

e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

LIVRO DIGITAL (E-book) Números Triangulares e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.