


Dispondo números naturais em uma coluna e em uma linha e posteriormente multiplicando um pelo outro, obtem-se o produto dos dois em cada cruzamento, conforme pode ser observado na tabuada abaixo, na qual são apresentadas outras interessantes propriedades numéricas .
Podemos também utilizar a Tabuada para fazer exercícios de cálculos mentais de multiplicação, adição, divisão e subtração.
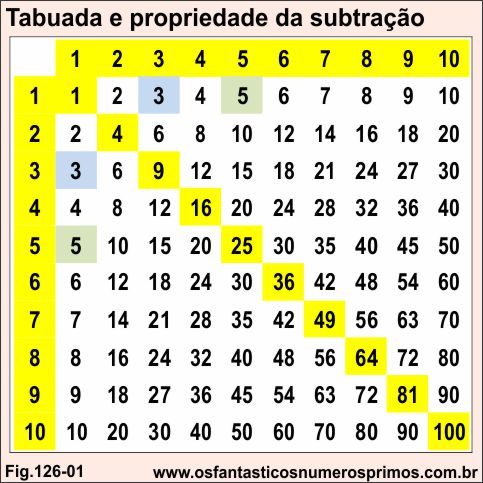
Na diagonal principal da Tabuada forma-se a sequência de números quadrados perfeitos: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ...
Subtraindo-se um quadrado sucessor de um quadrado antecessor, obtem-se um número ímpar:
Exemplos:
a) 4 - 1= 3
b) 9 - 4 = 5
c) 16 - 9 = 7
Uma outra propriedade que se apresenta na Tabuada é a da Subtração.
Exemplo 1)
Querendo se saber a diferença entre dois números quadrados consecutivos, por exemplo: 1 e 4, o resultado aparece tanto na primeira linha horizontal quanto na primeira linha vertical, sem precisar montarmos a conta de subtração.
a) marca-se os números quadrados em amarelo:
1 e 4
b) segue-se na diagonal a partir de 4, e encontramos a diferença 3, marcado em azul.
| Tabuada | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |||||||||
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |||||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |||||||||
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |||||||||
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |||||||||
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |||||||||
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |||||||||
Exemplo 2)
Querendo se saber a diferença entre dois números quadrados consecutivos, por exemplo: 4 e 9, o resultado aparece tanto na primeira linha horizontal quanto na primeira linha vertical, sem precisar montarmos a conta de subtração.
a) marca-se o números quadrados em amarelo:
4 e 9
b) segue-se na diagonal a partir de 9, e encontramos a diferença 5, marcado em azul.
| Tabuada | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |||||||||
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |||||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |||||||||
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |||||||||
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |||||||||
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |||||||||
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |||||||||
Exemplo 1)
Querendo se saber a diferença entre dois números quadrados não consecutivos, por exemplo: 1 e 9, o resultado aparece a partir da primeira linha horizontal quanto na primeira linha vertical, seguindo na diagonal da primeira diferença entre os quadrados 1 e 4 que é o 3.
a) marca-se os números quadrados em amarelo:
1 e 9;
b) a partir da diferença 3 (marcado em verde) entre os quadrados 4 e 1, segui-se na diagonal até 8;
c) 8 é a diferença entre os quadrados não consecutivos 1 e 9;
d) 8 se encontra na mesma diagonal do quadrado 9.
| Tabuada | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |||||||||
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |||||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |||||||||
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |||||||||
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |||||||||
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |||||||||
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |||||||||
Exemplo 2)
Querendo se saber a diferença entre dois números quadrados não consecutivos, por exemplo: 4 e 16, o resultado aparece a partir da primeira linha horizontal quanto na primeira linha vertical, seguindo na diagonal da primeira diferença entre os quadrados 4 e 9 que é o 5.
a) marca-se os números quadrados em amarelo:
4 e 16;
b) a partir da diferença 5 (marcado em verde) entre os quadrados 4 e 9, seguimos na diagonal até 12;
c) 12 é a diferença entre os quadrados não consecutivos 4 e 16;
d) 12 se encontra na mesma diagonal do quadrado 16.
| Tabuada | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | |||||||||
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | |||||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | |||||||||
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |||||||||
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | |||||||||
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | |||||||||
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | |||||||||
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | |||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |||||||||
O interessante neste estudo é que as diferenças entre dois números, sejam eles números quadrados ou não, se encontram em diagonais.
Experimente, treine você também!
Autor: Ricardo Silva - janeiro/2017
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato