


Podemos desenhar triângulos equiláteros de variadas dimensões e inscrever em cada um deles outros triângulos equiláteros, marcando o ponto médio em cada um dos seus lados e unindo-os com segmentos de retas conforme exemplos da fig. 086-01.

Números triangulares, também chamados números figurados, são números que podem ser representados com figuras de triângulos atravês de arranjos de pontos.
Nos exemplos a seguir, os triângulos equiláteros estão construídos por pontos, e diferentemente dos triângulos equiláteros desenhados com auxílio de instrumentos de desenho tais como: lápis, compasso e esquadros, nem todos os triângulos equiláteros construídos por pontos podem ter outros triângulos equiláteros inscritos neles próprios.
Os triângulos equiláteros construídos por pontos e que podem ter triângulos inscritos neles próprios apresentam um diferencial quantos aos outros triângulo equiláteros, as suas bases têm quantidades de pontos ímpares.
Outra regularidade existente na construção de triângulo equilátero por meio de arranjos de pontos é que triângulos cujas quantidades de pontos são números perfeitos também são os que podem ter outros triângulos inscritos.
O número 1, por convenção, é um número triangular, um número quadrado perfeito, um número pentagonal, um número hexagonal e assim por diante.
A base possui 1 ponto.
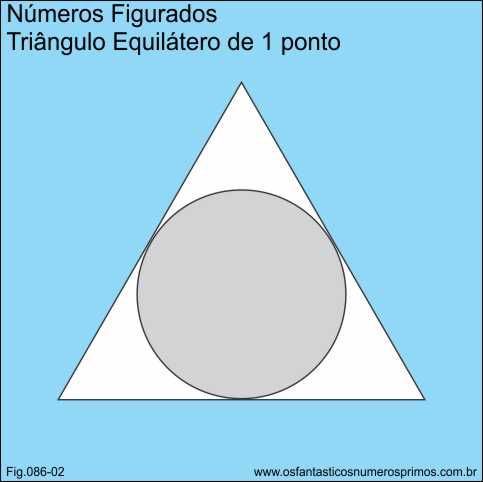
O número 3 é um número triangular.
A base possui 2 pontos.
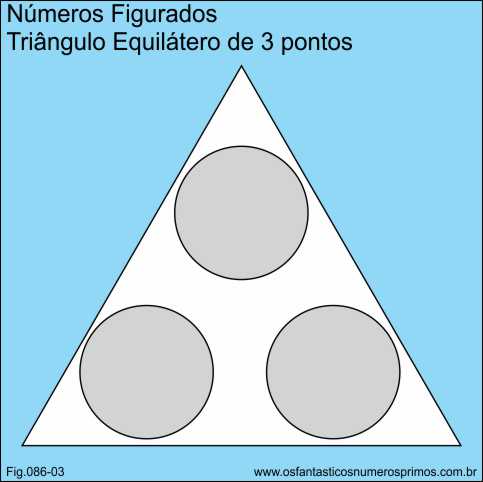
O número 6 é um número triangular.
A base possui 3 pontos é de quantidade ímpar, portanto tem a propriedade de ter um triângulo figurado inscrito.
O triângulo equilátero inscrito é de 3 pontos.

O número 10 é um número triangular.
A base possui 4 pontos.

O número 15 é um número triangular.
A base possui 5 pontos é de quantidade ímpar, portanto tem a propriedade de ter um triângulo figurado inscrito.

O número 21 é um número triangular.
A base possui 6 pontos.
O triângulo equilátero inscrito é de 6 pontos.

O número 28 é um número triangular.
A base possui 7 pontos e é de quantidade ímpar, portanto tem a propriedade de ter um triângulo figurado inscrito.
O triângulo equilátero inscrito é de 10 pontos.

O número 36 é um número triangular.
A base possui 8 pontos.

Conforme os exemplos expostos, existe uma acomodação natural em que um triângulo equilátero figurado poder ter um outro triângulo equilátero figurado inscrito, estudos mais apurados sobre esse assunto se encontra no livro digital Números Triangulares e Sequências Numéricas.
Autor: Ricardo Silva
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato