


O Teorema de Pitágoras (a² = b² + c² ) é uma das fórmulas mais importantes e muito utilizada para se efetuarem cálculos aritméticos, algébricos e trigonométricos a partir de um triângulo retângulo.
A sua estrutura carrega grandes quantidades de informações e conceitos matemáticos que se relacionam entre si.
Com o Teorema de Pitágoras, para citar alguns exemplos, são possíveis de se:
a) calcular lados, áreas e alturas de triângulos retângulos;
b) calcular lados, áreas e alturas das mais diversas figuras geométricas regulares;
c) calcular distâncias acessíveis e distâncias inacessíveis, como distâncias planetárias: da Terra ao Sol; da Terra a Lua; da Lua ao Sol, etc.
Neste estudo são demonstrados novas relações numéricas entre o Teorema de Pitágoras e construções geométricas com a sequência de números triangulares, bem como, com números irracionais e números primos.
No cápitulo 1 Revendo Números do livro Realidade Matemática 8° ano são apresentados modelos matemáticos cujos objetivos são demonstrar conceitos iniciais sobre números racionais e irracionais, no qual apresenta o sequinte questionamento:
Qual é a área de um quadrado de lado 1 e qual é o lado de um quadrado de área 2?
Para mais informações veja matérias relacionadas.
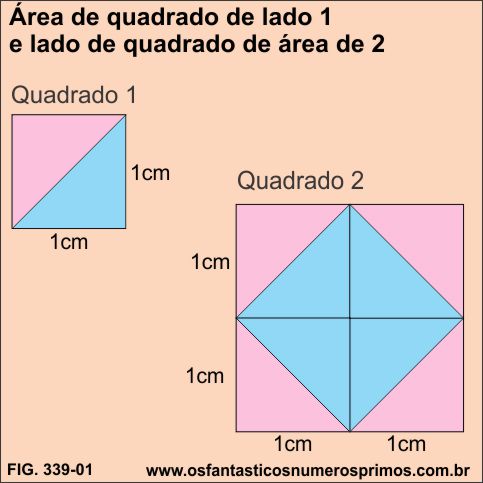
Fonte: Adaptado do livro Realidade Matemática - 8° ano/Gelson Iezzi, Owaldo Dolce, Antonio Machado - 6a edi - São Paulo - Atual , 2009.
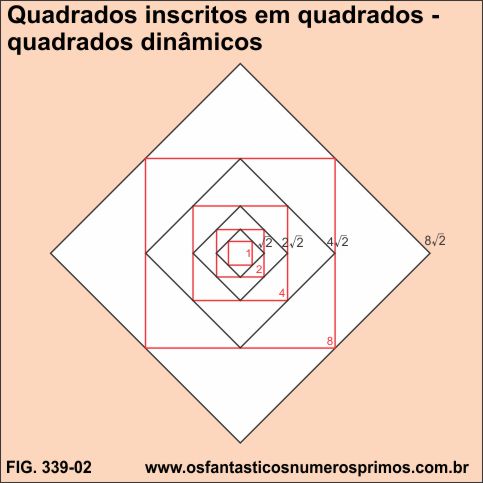
Há quatro métodos de construções de quadrados dinâmicos, no exemplo, construções de quadrados proporcionais a partir do ponto médio de cada lado de cada quadrado.
Os quadrados formados a partir do ponto médio de cada um de seus lados geram quadrados, ora com lados de números inteiros, ora quadrados com lados de números irracionais.
Para mais informações, veja abaixo, Matérias Relacionadas!
Na demonstração do Teorema de Pitágoras, com a qual os chineses o chamam de Teorema Gou-gu, publicada no livro Chou Pei Suan Ching, o quadrado de área 25 se encontra em um quadrado quadriculado e é formado por 4 triângulos retângulos cujas hipotenusas formam os lados do quadrado inscrito e um quadradinho central.

Fonte: https://pt.wikipedia.org
Cada triângulo retângulo possui a seguinte área:
3 x 4 = 12
12 / 2 = 6
Reparar que há um quadradinho no centro do quadrado maior.
Então, 4 triângulos x 6 (área) = 24
24 + 1 (quadradinho central) = 25 (área do quadrado maior)
Partindo-se dos exemplos expostos e principalmente da demonstração chinesa do Teorema de Pitágoras, quando é que um quadrado inscrito em um quadrado terá a sua área e consequentemente a sua raiz quadrada números inteiros ?
Assim como na antiga China, também já era de conhecimento das antigas civilizações mesopotâmicas e egípcia a manipulação do Terno Pitagórico 3, 4, 5 e sua relação com o triângulo retângulo.
Construindo-se um quadrado quadriculado de lado 3 e área 9 e inscrevendo um outro quadrado, qual é a área e o lado do quadrado inscrito?
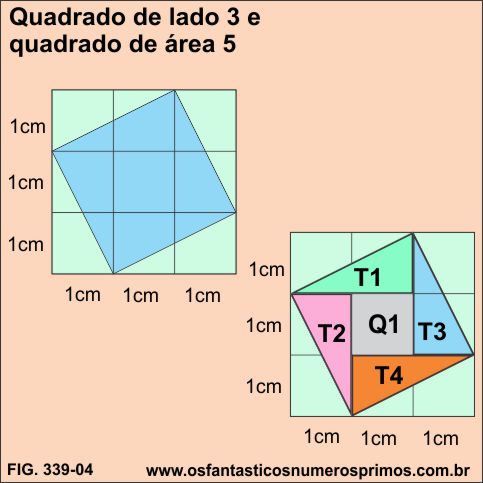
área de cada triângulo: T1, T2, T3 e T4.
base x altura / 2
4 x ( 2 x 1 / 2)
4 x 1 = 4
área do quadrado Q1 = 1 x 1 = 1
Portanto a área do quadrado azul é igual a 5cm² (4 + 1) e a
medida do seu lado é √5 = 2,23..., um número irracional.
Interessante observar que:
a) 3 e 5 fazem parte do Terno Pitagórico Primitivo de Ordem Triangular 3-4-5;
b) 3 é número de Fermat da forma 4x + 3;
c) 5 é número de Fermat da forma 4x + 1;
Construindo-se um quadrado quadriculado de lado 5 e área 25 e inscrevendo um outro quadrado, qual é a área e o lado do quadrado inscrito?
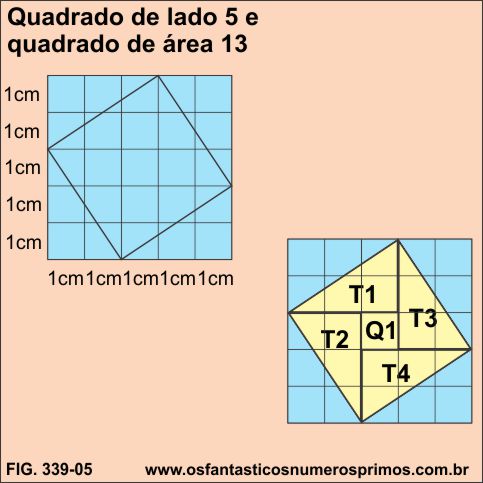
área de cada triângulo: T1, T2, T3 e T4.
base x altura / 2
4 x ( 3 x 2 / 2)
4 x 3 = 12
área do quadrado Q1 = 1 x 1 = 1
Portanto a área do quadrado amarelo é igual a 13 cm² (12 + 1) e a
medida do seu lado é √13 = 3,6055..., um número irracional.
Interessante observar que:
a) 5 e 13 fazem parte do Terno Pitagórico Primitivo de Ordem Triangular 5-12-13;
b) 5 é número de Fermat da forma 4x + 1;
c) 13 é número de Fermat da forma 4x + 1;
Construindo-se um quadrado quadriculado de lado 7 e área 49 e inscrevendo um outro quadrado, qual é a área e o lado do quadrado inscrito?
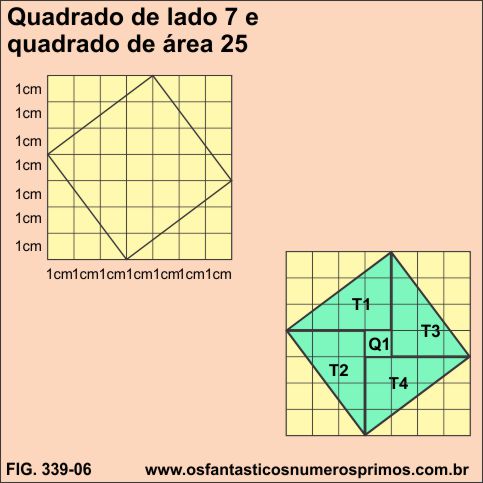
área de cada triângulo: T1, T2, T3 e T4.
base x altura / 2
4 x ( 4 x 3 / 2)
4 x 6 = 24
área do quadrado Q1 = 1 x 1 = 1
Portanto a área do quadrado amarelo é igual a 25 cm² (24 + 1) e a
medida do seu lado é √25 = 5, um número inteiro.
Interessante observar que 7 e 25 fazem parte do Terno Pitagórico Primitivo de Ordem Triangular 3-4-5.
Parafraseando...
... Bhaskara Akaria (1114-1185) matemático indiano, também conhecido como Bhaskaracharya.
Nota: Não confudir com o também matemático indiano Bhaskara I que viveu no século VI.
Aqui está!
Contemple!
Veja!...,
pois a construção geométrica no livro chinês Chou Pei Suan Ching com a demostração do Teorema de Pitágoras com quadrado inscrito em um quadrado é uma das quatro variantes que podem ser construídas com um quadrado de lado unitário central conforme explanações e cálculos a seguir.
As expressões numéricas utilizadas para os cálculos de áreas e lados de quadrados inscritos em quadrados nos exemplos apresentados, têm em suas formações termos da sequência de números triangulares, vejamos:
cálculo 1
4 x ( 2 x 1 / 2)
4 x 1 = 4
4 multiplicado pelo triangular 1
cálculo 2
4 x ( 3 x 2 / 2)
4 multiplicado pelo triangular 3
cálculo 3
4 x ( 4 x 3 / 2)
4 multiplicado pelo triangular 6.
6 é um número triangular e perfeito.
Nos cálculos encontramos o primeiro quadrado inscrito em um quadrado cujas área e lado são números inteiros.
Simples coincidência ou há relação entre a construção geométrica com número perfeito e número inteiro?
Montando-se tabela a partir da expressão numérica acima e efetuando-se os cálculos verifica-se que entre os 1000 primeiros números triangulares multiplicados por 4 geram 4 sequências que correspondem às areas e lados de quadrados inscritos em quadrados formados por números inteiros, os demais resultados geram números irracionais.
| Número 4 | ||||||||
| multiplicado por | ||||||||
| número triangular | ||||||||
| área do | ||||||||
| quadrado | ||||||||
| multiplicação | ||||||||
| triangular | produto | soma | raiz | |||||
| 4 | x | 1 | = | 4 | 1 | = | 5 | 2,236068 |
| 4 | x | 3 | = | 12 | 1 | = | 13 | 3,605551 |
| 4 | x | 6 | = | 24 | 1 | = | 25 | 5 |
| 4 | x | 10 | = | 40 | 1 | = | 41 | 6,403124 |
| 4 | x | 15 | = | 60 | 1 | = | 61 | 7,81025 |
| 4 | x | 21 | = | 84 | 1 | = | 85 | 9,219544 |
| 4 | x | 28 | = | 112 | 1 | = | 113 | 10,63015 |
| 4 | x | 36 | = | 144 | 1 | = | 145 | 12,04159 |
| 4 | x | 45 | = | 180 | 1 | = | 181 | 13,45362 |
| 4 | x | 55 | = | 220 | 1 | = | 221 | 14,86607 |
| 4 | x | 66 | = | 264 | 1 | = | 265 | 16,27882 |
| 4 | x | 78 | = | 312 | 1 | = | 313 | 17,69181 |
| 4 | x | 91 | = | 364 | 1 | = | 365 | 19,10497 |
| 4 | x | 105 | = | 420 | 1 | = | 421 | 20,51828 |
| 4 | x | 120 | = | 480 | 1 | = | 481 | 21,93171 |
| 4 | x | 136 | = | 544 | 1 | = | 545 | 23,34524 |
| 4 | x | 153 | = | 612 | 1 | = | 613 | 24,75884 |
| 4 | x | 171 | = | 684 | 1 | = | 685 | 26,1725 |
| 4 | x | 190 | = | 760 | 1 | = | 761 | 27,58623 |
| 4 | x | 210 | = | 840 | 1 | = | 841 | 29 |
| 4 | x | 231 | = | 924 | 1 | = | 925 | 30,41381 |
| 4 | x | 253 | = | 1012 | 1 | = | 1013 | 31,82766 |
| 4 | x | 276 | = | 1104 | 1 | = | 1105 | 33,24154 |
| 4 | x | 300 | = | 1200 | 1 | = | 1201 | 34,65545 |
| 4 | x | 325 | = | 1300 | 1 | = | 1301 | 36,06938 |
| 4 | x | 351 | = | 1404 | 1 | = | 1405 | 37,48333 |
| 4 | x | 378 | = | 1512 | 1 | = | 1513 | 38,8973 |
| 4 | x | 406 | = | 1624 | 1 | = | 1625 | 40,31129 |
| 4 | x | 435 | = | 1740 | 1 | = | 1741 | 41,72529 |
| 4 | x | 465 | = | 1860 | 1 | = | 1861 | 43,13931 |
| 4 | x | 496 | = | 1984 | 1 | = | 1985 | 44,55334 |
| 4 | x | 528 | = | 2112 | 1 | = | 2113 | 45,96738 |
| 4 | x | 561 | = | 2244 | 1 | = | 2245 | 47,38143 |
| 4 | x | 595 | = | 2380 | 1 | = | 2381 | 48,79549 |
| 4 | x | 630 | = | 2520 | 1 | = | 2521 | 50,20956 |
| 4 | x | 666 | = | 2664 | 1 | = | 2665 | 51,62364 |
| 4 | x | 703 | = | 2812 | 1 | = | 2813 | 53,03772 |
| 4 | x | 741 | = | 2964 | 1 | = | 2965 | 54,45181 |
| 4 | x | 780 | = | 3120 | 1 | = | 3121 | 55,86591 |
| 4 | x | 820 | = | 3280 | 1 | = | 3281 | 57,28001 |
| 4 | x | 861 | = | 3444 | 1 | = | 3445 | 58,69412 |
| 4 | x | 903 | = | 3612 | 1 | = | 3613 | 60,10824 |
| 4 | x | 946 | = | 3784 | 1 | = | 3785 | 61,52235 |
| 4 | x | 990 | = | 3960 | 1 | = | 3961 | 62,93648 |
| 4 | x | 1035 | = | 4140 | 1 | = | 4141 | 64,3506 |
| 4 | x | 1081 | = | 4324 | 1 | = | 4325 | 65,76473 |
| 4 | x | 1128 | = | 4512 | 1 | = | 4513 | 67,17887 |
| 4 | x | 1176 | = | 4704 | 1 | = | 4705 | 68,593 |
| 4 | x | 1225 | = | 4900 | 1 | = | 4901 | 70,00714 |
| 4 | x | 1275 | = | 5100 | 1 | = | 5101 | 71,42129 |
| 4 | x | 1326 | = | 5304 | 1 | = | 5305 | 72,83543 |
| 4 | x | 1378 | = | 5512 | 1 | = | 5513 | 74,24958 |
| 4 | x | 1431 | = | 5724 | 1 | = | 5725 | 75,66373 |
| 4 | x | 1485 | = | 5940 | 1 | = | 5941 | 77,07788 |
| 4 | x | 1540 | = | 6160 | 1 | = | 6161 | 78,49204 |
| 4 | x | 1596 | = | 6384 | 1 | = | 6385 | 79,9062 |
| 4 | x | 1653 | = | 6612 | 1 | = | 6613 | 81,32035 |
| 4 | x | 1711 | = | 6844 | 1 | = | 6845 | 82,73452 |
| 4 | x | 1770 | = | 7080 | 1 | = | 7081 | 84,14868 |
| 4 | x | 1830 | = | 7320 | 1 | = | 7321 | 85,56284 |
| 4 | x | 1891 | = | 7564 | 1 | = | 7565 | 86,97701 |
| 4 | x | 1953 | = | 7812 | 1 | = | 7813 | 88,39118 |
| 4 | x | 2016 | = | 8064 | 1 | = | 8065 | 89,80535 |
| 4 | x | 2080 | = | 8320 | 1 | = | 8321 | 91,21952 |
| 4 | x | 2145 | = | 8580 | 1 | = | 8581 | 92,63369 |
| 4 | x | 2211 | = | 8844 | 1 | = | 8845 | 94,04786 |
| 4 | x | 2278 | = | 9112 | 1 | = | 9113 | 95,46203 |
| 4 | x | 2346 | = | 9384 | 1 | = | 9385 | 96,87621 |
| 4 | x | 2415 | = | 9660 | 1 | = | 9661 | 98,29039 |
| 4 | x | 2485 | = | 9940 | 1 | = | 9941 | 99,70456 |
| 4 | x | 2556 | = | 10224 | 1 | = | 10225 | 101,1187 |
| 4 | x | 2628 | = | 10512 | 1 | = | 10513 | 102,5329 |
| 4 | x | 2701 | = | 10804 | 1 | = | 10805 | 103,9471 |
| 4 | x | 2775 | = | 11100 | 1 | = | 11101 | 105,3613 |
| 4 | x | 2850 | = | 11400 | 1 | = | 11401 | 106,7755 |
| 4 | x | 2926 | = | 11704 | 1 | = | 11705 | 108,1896 |
| 4 | x | 3003 | = | 12012 | 1 | = | 12013 | 109,6038 |
| 4 | x | 3081 | = | 12324 | 1 | = | 12325 | 111,018 |
| 4 | x | 3160 | = | 12640 | 1 | = | 12641 | 112,4322 |
| 4 | x | 3240 | = | 12960 | 1 | = | 12961 | 113,8464 |
| 4 | x | 3321 | = | 13284 | 1 | = | 13285 | 115,2606 |
| 4 | x | 3403 | = | 13612 | 1 | = | 13613 | 116,6748 |
| 4 | x | 3486 | = | 13944 | 1 | = | 13945 | 118,0889 |
| 4 | x | 3570 | = | 14280 | 1 | = | 14281 | 119,5031 |
| 4 | x | 3655 | = | 14620 | 1 | = | 14621 | 120,9173 |
| 4 | x | 3741 | = | 14964 | 1 | = | 14965 | 122,3315 |
| 4 | x | 3828 | = | 15312 | 1 | = | 15313 | 123,7457 |
| 4 | x | 3916 | = | 15664 | 1 | = | 15665 | 125,1599 |
| 4 | x | 4005 | = | 16020 | 1 | = | 16021 | 126,5741 |
| 4 | x | 4095 | = | 16380 | 1 | = | 16381 | 127,9883 |
| 4 | x | 4186 | = | 16744 | 1 | = | 16745 | 129,4025 |
| 4 | x | 4278 | = | 17112 | 1 | = | 17113 | 130,8167 |
| 4 | x | 4371 | = | 17484 | 1 | = | 17485 | 132,2309 |
| 4 | x | 4465 | = | 17860 | 1 | = | 17861 | 133,6451 |
| 4 | x | 4560 | = | 18240 | 1 | = | 18241 | 135,0592 |
| 4 | x | 4656 | = | 18624 | 1 | = | 18625 | 136,4734 |
| 4 | x | 4753 | = | 19012 | 1 | = | 19013 | 137,8876 |
| 4 | x | 4851 | = | 19404 | 1 | = | 19405 | 139,3018 |
| 4 | x | 4950 | = | 19800 | 1 | = | 19801 | 140,716 |
| 4 | x | 5050 | = | 20200 | 1 | = | 20201 | 142,1302 |
| 4 | x | 5151 | = | 20604 | 1 | = | 20605 | 143,5444 |
| 4 | x | 5253 | = | 21012 | 1 | = | 21013 | 144,9586 |
| 4 | x | 5356 | = | 21424 | 1 | = | 21425 | 146,3728 |
| 4 | x | 5460 | = | 21840 | 1 | = | 21841 | 147,787 |
| 4 | x | 5565 | = | 22260 | 1 | = | 22261 | 149,2012 |
| 4 | x | 5671 | = | 22684 | 1 | = | 22685 | 150,6154 |
| 4 | x | 5778 | = | 23112 | 1 | = | 23113 | 152,0296 |
| 4 | x | 5886 | = | 23544 | 1 | = | 23545 | 153,4438 |
| 4 | x | 5995 | = | 23980 | 1 | = | 23981 | 154,858 |
| 4 | x | 6105 | = | 24420 | 1 | = | 24421 | 156,2722 |
| 4 | x | 6216 | = | 24864 | 1 | = | 24865 | 157,6864 |
| 4 | x | 6328 | = | 25312 | 1 | = | 25313 | 159,1006 |
| 4 | x | 6441 | = | 25764 | 1 | = | 25765 | 160,5148 |
| 4 | x | 6555 | = | 26220 | 1 | = | 26221 | 161,929 |
| 4 | x | 6670 | = | 26680 | 1 | = | 26681 | 163,3432 |
| 4 | x | 6786 | = | 27144 | 1 | = | 27145 | 164,7574 |
| 4 | x | 6903 | = | 27612 | 1 | = | 27613 | 166,1716 |
| 4 | x | 7021 | = | 28084 | 1 | = | 28085 | 167,5858 |
| 4 | x | 7140 | = | 28560 | 1 | = | 28561 | 169 |
| www.osfantasticosnumerosprimos.com.br | ||||||||
4 Expressões numéricas relacionadas à construções geométricas de quadrados inscritos em quadrados cujos resultados são números inteiros.
| área do | ||||||||
| quadrado | ||||||||
| triangular | produto | soma | raiz | |||||
| 4 | x | 6 | = | 24 | 1 | = | 25 | 5 |
| 4 | x | 210 | = | 840 | 1 | = | 841 | 29 |
| 4 | x | 7140 | = | 28560 | 1 | = | 28561 | 169 |
| 4 | x | 242556 | = | 970224 | 1 | = | 970225 | 985 |
Observação: as tabela aqui demonstradas, apresentam relações com:
a) o Algoritimo Escada de Theon;
b) números da forma 4x + 1;
c) números triangulares retangulares.
Veja Matérias Relacionadas para mais informações.
Autor: Ricardo Silva - abril/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato