Página de estudos de matemática e sequências numéricas

Quadrados e triângulos inscritos em quadrados e números primos - 338

Números irracionais são números que possuem infinitos algarismos não periódicos após a vírgula.

Os números irracionais não podem ser gerados da divisão de dois números inteiros.

Através de processo geométrico podemos determinar um ponto em que um número irracional ocupa numa reta numérica.

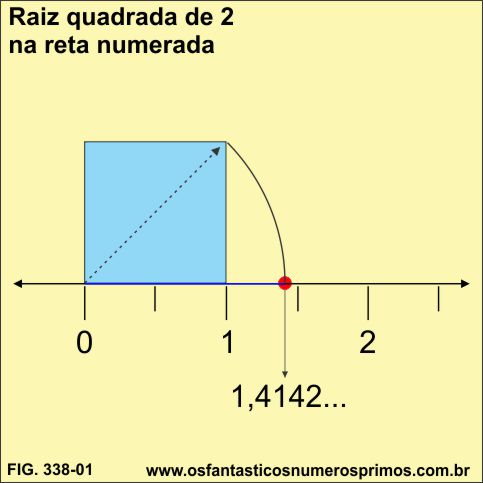
a) desenha um quadrado de lado unitário sobre a reta numerada;

b) traça-se um arco de circunferência com centro no ponto 0 (zero) da reta e extremidade no vértice superior direito do quadrado até a reta numerada;

c) a intersecção do arco de circunferência com a reta numerada corresponde a √2, que é aproximadamente 1,4142...

Determinando áreas e lados de quadrados

No cápitulo 1 Revendo Números do livro Realidade Matemática 8° ano são apresentados modelos matemáticos cujos objetivos são demonstrar conceitos iniciais sobre números racionais e irracionais.

Fazendo análises desses modelos matemáticos, eles revelam interessantes regularidades tanto nas configurações geométricas quanto nas sequências numéricas que eles geram.

Fonte: Adaptado do livro Realidade Matemática - 8° ano/Gelson Iezzi, Owaldo Dolce, Antonio Machado - 6a edi - São Paulo - Atual , 2009.

Quadrado 1

Os lados do Quadrado 1 medem 1cm.

Traçando-se uma diagonal, dividi-se o quadrado em duas partes.

Responda:

Qual é a área do quadrado?

Qual é a área de cada parte?

Quadrado 2

Juntando-se quatro quadradinhos de 1cm de lado, forma-se um quadrado maior de 2cm de lado.

No interior do quadrado maior, forma-se um outro quadrado (cor azul)

Responda:

Qual é a área do quadrado azul?

Quanto medem os seus lados?

A medida dos lados é um número inteiro?

É um número racional (fracionário)?

Quadrado de área 5 inscrito em quadrado de lado 3

No quadrado de lado 3, qual é a medida aproximada do lado do quadrado de área 5?

Demarcando o quadrado de área 5, podemos decompô-lo em 4 triângulos e 1 quadrado menor com as seguintes áreas:

Método 1

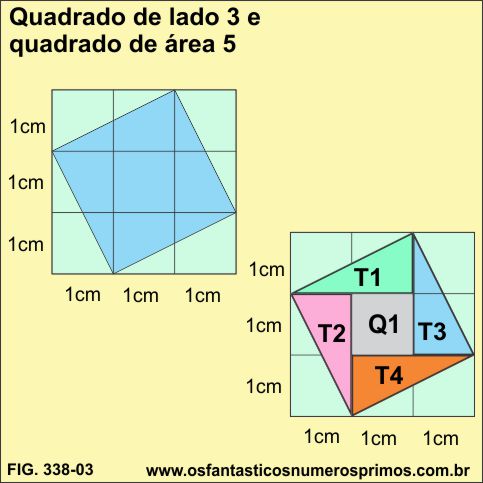
área de cada triângulo: T1, T2, T3 e T4.

base x altura / 2

4 x ( 2 x 1 / 2)

4 x 1 = 4

área do quadrado Q1 = 1 x 1 = 1

Portanto a área do quadrado azul é igual a 5cm² (4 + 1)

medida do seu lado é √5 = 2,23..., um número irracional.

Método 2

área do quadrado maior (cor verde): 3 x 3 = 9

área de cada triângulo: T1, T2, T3 e T4.

base x altura / 2

4 x ( 2 x 1 / 2)

4 x 1 = 4

área dos 4 triângulos subtraídas do quadrado maior é igual a área do quadrado (cor azul)

9 - 4 = 5

medida do lado do quadrado (cor azul)

√5 = 2,23..., um número irracional.

Quadrado de área 17 inscrito em quadrado de lado 5

No quadrado de lado 5, qual é a medida aproximada do lado do quadrado de área 17 ?

Demarcando o quadrado de área 17, podemos decompô-lo em 4 triângulos e 1 quadrado menor com as seguintes áreas:

Método 1

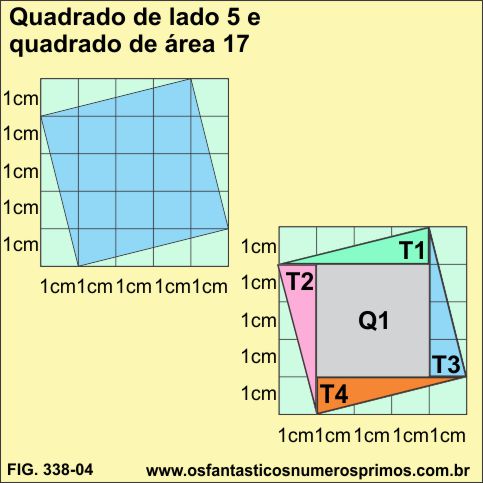
área de cada triângulo: T1, T2, T3 e T4

base x altura / 2

4 x ( 4 x 1 / 2)

4 x 2 = 8

área do quadrado Q1 = 3 x 3 = 9

Portanto a área do quadrado azul é igual a 17cm² (8 + 9).

Medida do lado √17 = 4,12...

Método 2

área do quadrado maior (cor verde): 5 x 5 = 25

área de cada triângulo: T1, T2, T3 e T4.

base x altura / 2

4 x ( 4 x 1 / 2)

4 x 2 = 8

área dos 4 triângulos subtraídas do quadrado maior é igual a área do quadrado (cor azul)

25 - 8 = 17

medida do lado do quadrado (cor azul)

√17 = 4,1231..., um número irracional.

A partir dos modelos matemáticos e cálculos apresentados é possível generalizar e formar expressões aritméticas que nos forneçam números que extraídos suas raízes quadradas deem como resultados números irracionais.

Expressão aritmética 1 - quadrados e triângulos inscritos em quadrados

Um número quadrado ímpar somado com o dobro de sua raiz quadrada e duas unidades tem como resultado um número que extraído a sua raiz quadrada tem como resultado um número irracional.

Exemplo 1)

1² + 2 + 2 =

1 + 2 + 2 = 5 (número primo)

√5 = 2,23...

Exemplo 2)

3² + 6 + 2 =

9 + 6 + 2 = 17 (número primo)

√17 = 4,1231...

Exemplo 3)

5² + 10 + 2 =

25 + 10 + 2 = 37 (número primo)

√37 = 6,0827...

Cálculos efetuados e tabulados com os 1000 primeiros números quadrados ímpares perfeitos demonstram que os lados dos quadrados inscritos são todos números irracionais.

A seguinte tabela apresenta os 50 primeiros cálculos.

Expressão numérica 2 - quadrados e triângulos inscritos em quadrados

O dobro de uma raiz quadrada ímpar subtraída duas unidades e posteriomente subraída do número quadrado ímpar correspondente igual ou maior que 9 tem como resultado um número que extraído a sua raiz quadrada tem como resultado um número irracional.

Exemplo 1)

3² - (6 - 2) =

= 9 - 4

= 5 (número primo)

√5 = 2,23...

Exemplo 2)

5² - (10 - 2) =

= 25 - 8

= 17 (número primo)

√17 = 4,1231...

Exemplo 3)

7² - (14 - 2) =

= 49 - 12

= 37 (número primo)

√37 = 6,0827...

Cálculos efetuados e tabulados com os 1000 primeiros números quadrados ímpares perfeitos demonstram que os lados dos quadrados inscritos são todos números irracionais, com exceção do primeiro cálculo cuja raiz quadrada é 1.

A seguinte tabela apresenta os 50 primeiros cálculos.

Autor: Ricardo Silva - abril/2021

Fontes Bibliográficas:

Realidade Matemática - 8° ano/Gelson Iezzi, Owaldo Dolce, Antonio Machado - 6a edi - São Paulo - Atual , 2009.

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

011-estudos-101-o-quadrado-sequencias-numericas

011-estudos-107-quadrado-inscrito-circunferencia

011-estudos-115-quadrados-dinamicos

011-estudos-143-quadrado-inscrito-e-circunscrito-numa-circunferencia

Livro digital (e-book)

Progressões Aritméticas e Geométricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)

Estudos de Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

RECEBAM GRATUITAMENTE

O E-BOOK

TRIÂNGULO RETÂNGULO:

 

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Manual Digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.