Zhoubi suanjing (Clássico Aritmético do Gnomon e os Caminhos Circulares do Céu) é um livro chinês sobre astronomia e matemática datado de aproximadamente 100 aC.
"Zhou" refere-se à antiga dinastia Zhou (1046–256 aC).
"Bi" significa coxa e, de acordo com o livro, refere-se ao gnômon do relógio de sol.
"Suan Jing" "clássico da aritmética".
Chou Pi Suan Ching - transliteração.
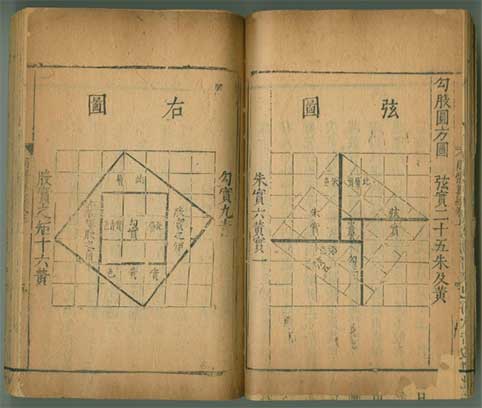
A imagem de detalhe do livro é de uma cópia da dinastia Ming impressa em 1603. Esses diagramas foram adicionados ao texto original em algum ponto na tentativa de ilustrar uma prova de dissecação do "Teorema de Pitágoras", conhecido pelos chineses como teorema de Gou-gu.
Na página à direita, diagrama de um prova visual do Teorema de Pitágoras.
Neste estudo os diagramas de triângulos serão referenciados seguindo o exemplo: Triângulo 3-4-5 de Gou-Gu, preservando desta forma o modo como os chineses o denominam, assim como nós ocidentais estamos acostumados a denominar: Teorema de Pitágoras, Triângulo Pitagórico, Triângulo de Pitágoras, Ternos Pitagóricos, Tripla Pitagórica, etc.
Fonte: https://www.maa.org/press/
Os estudos aqui apresentados são complementares a outros estudos publicados aqui WebSite Os Fantáticos Números Primos.
Veja matérias relacionadas abaixo, para mais informações.
As construções de diagramas quadriculados com retângulos e triângulos retângulos inscritos aqui referenciados para se contruirem outros triângulos retângulos, possuem em suas estruturas interessantes propriedades geométricas e aritméticas:
a) de que os cálculos para se saber as medidas dos lados de um triângulo retângulo estão estritamente relacionados com o quadradinho central do diagrama;
b) de que a diferença entre cateto menor e cateto maior tem como a media do lado do quadradinho central;
c) de que os cálculos referente a lados de triângulos retângulo podem ser efetuados aritmeticamente.
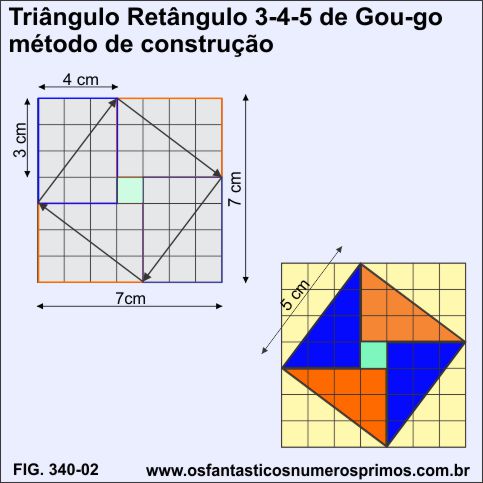
Para a construção de um Triângulo Retângulo 3-4-5 de Gou-gu, segue-se as seguintes etapas:
a) desenha-se um quadrado quadriculado de 7 cm de lado;
b) desenham-se 4 retângulos de base 4 cm e altura 3 cm, de forma que um par fique na vertical e outro na horizontal;
c) traça-se a diagonal em cada um dos retângulos;
d) finalizando, desta forma, com um quadrado de lado de 5 cm inscrito no quadrado de lado de 7 cm.
Observação importante: no centro do quadrado inscrito, forma-se um quadrado de lado de 1cm.
Cálculos para se saber a área do quadrado inscrito
Área do quadrado maior
7² = 49 cm²
Área de cada triângulo
(base x altura) / 2
(4 x 3) / 2 = 6
4 triângulos x 6 = 24 cm²
49 cm² - 24 cm² = 25 cm²
Resposta: A área do quadrado inscrito é 25 cm².
Cálculos para se saber a medida do lado do quadrado inscrito / hipotenusa.
Área de cada triângulo
(base x altura) / 2
(4 x 3) / 2 = 6
4 triângulos x 6 = 24 cm²
24 cm² + 1cm² (área do quadradinho central) = 25 cm²
√25 = 5cm
Resposta: O lado do quadrado inscrito é 5 cm.
Observação: 5cm também é a medida da hipotenusa no triângulo retângulo.
Cálculos para se saber a medida do cateto menor
5² = 25 cm²
25 cm² - 1 cm² (área do quadradinho central) = 24 cm²
24 cm² : (2 x 4) dobro do cateto maior
24 cm² : 8 = 3
Resposta: A medida do cateto menor é 3 cm.
Cálculos para se saber a medida do cateto maior
5² = 25 cm²
25 cm² - 1 cm² (área do quadradinho central) = 24 cm²
24 cm² : (2 x 3) dobro do cateto menor
24 cm² : 6 = 4
Resposta: A medida do cateto maior é 4 cm.
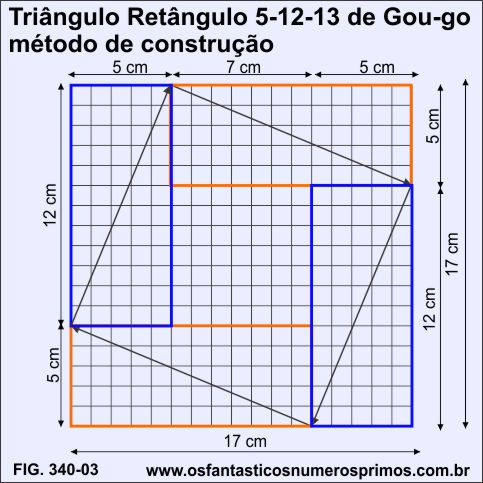
Para a construção de um Triângulo Retângulo 5-12-13 de Gou-gu, segue-se as seguintes etapas:
a) desenha-se um quadrado quadriculado de 17 cm de lado;
b) desenham-se 4 retângulos de base 12 cm e altura 5cm, de forma que um par fique na vertical e outro na horizontal;
c) traça-se a diagonal em cada um dos retângulos;
d) finalizando, desta forma, com um quadrado de lado de 13 cm inscrito no quadrado de lado de 17cm.
Observação importante: no centro do quadrado inscrito, forma-se um quadrado de lado de 7 cm.
Cálculos para se saber a área do quadrado inscrito
Área do quadrado maior
17² = 289 cm²
Área de cada triângulo
(base x altura) / 2
(12 x 5) / 2 = 30
4 triângulos x 30 = 120 cm²
289 cm² - 120 cm² = 169 cm²
Resposta: A área do quadrado inscrito é 169 cm².
Cálculos para se saber a medida do lado do quadrado inscrito / hipotenusa.
Área de cada triângulo
(base x altura) / 2
(12 x 5) / 2 = 30
4 triângulos x 30 = 120 cm²
120 cm² + 49 cm² (área quadrado central) = 169 cm²
√169 = 13
Resposta: O lado do quadrado inscrito é 13 cm.
Cálculos para se saber a medida do cateto menor
13² = 169 cm²
169 cm² - 49 cm² (área do quadrado central) = 120 cm²
120 cm² : (2 x 12) dobro do cateto maior
120 cm² : 24 = 5
Resposta: A medida do cateto menor é 5 cm.
Cálculos para se saber a medida do cateto maior
13² = 169 cm²
169 cm² - 49 cm² (área do quadrado central) = 120 cm²
120 cm² : (2 x 5) dobro do cateto maior
120 cm² : 10 = 12
Resposta: A medida do cateto maior é 12 cm.
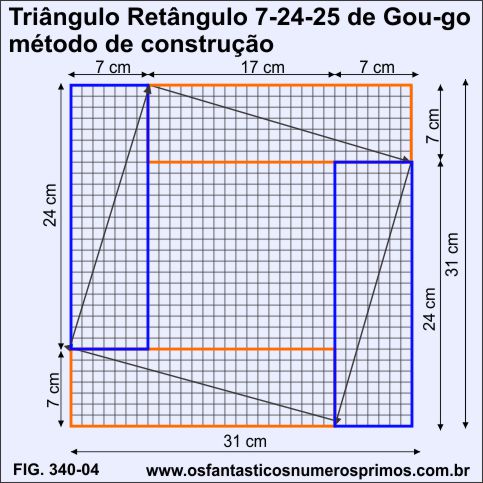
Para a construção de um Triângulo Retângulo 7-24-25 de Gou-gu, segue-se as seguintes etapas:
a) desenha-se um quadrado quadriculado de 31 cm de lado;
b) desenham-se 4 retângulos de base 24 cm e altura 7 cm, de forma que um par fique na vertical e outro na horizontal;
c) traça-se a diagonal em cada um dos retângulos;
d) finalizando, desta forma, com um quadrado de lado de 25 cm inscrito no quadrado de lado de 31 cm.
Observação importante: no centro do quadrado inscrito, forma-se um quadrado de lado de 17 cm.
Cálculos para se saber a área do quadrado inscrito
Área do quadrado maior
31² = 961 cm²
Área de cada triângulo
(base x altura) / 2
(24 x 7) / 2 = 84
4 triângulos x 84 = 336 cm²
961 cm² - 336 cm² = 625 cm²
Resposta: A área do quadrado inscrito é 625 cm².
Cálculos para se saber a medida do lado do quadrado inscrito / hipotenusa.
Área de cada triângulo
(base x altura) / 2
(24 x 7) / 2 = 84
4 triângulos x 84 = 336 cm²
336 cm² + 289 cm² (área do quadrado central) = 625 cm²
√625 = 25
Resposta: O lado do quadrado inscrito é 25 cm.
Cálculos para se saber a medida do cateto menor
25² = 625 cm²
625 cm² - 289 cm² (área do quadrado central) = 336 cm²
336 cm² : (2 x 24) dobro do cateto maior
336 cm² : 48 = 7
Resposta: A medida do cateto menor é 7 cm.
Cálculos para se saber a medida do cateto maior
25² = 625 cm²
625 cm² - 289 cm² (área do quadrado central) = 336 cm²
336 cm² : (2 x 7) dobro do cateto menor
336 cm² : 14 = 24
Resposta: A medida do cateto maior é 24 cm.
Autor: Ricardo Silva - abril/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
:https://pt.wikipedia.org/wiki/
https://www.maa.org/press/
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
