


Bhaskara (1114-1185) matemático indiano, também conhecido como Bhaskaracharya, Bhaskara Akaria.
Nota: Não confudir com o também matemático indiano Bhaskara I que viveu no século VI.
Bhaskara nasceu na cidade de Vijayapura, na Índia. Nasceu em uma tradicional família de astrólogos indianos, seguiu a tradição profissional da família, porém com uma orientação científica, dedicando-se mais à parte matemática e astronômica. Seus méritos foram logo reconhecidos e muito cedo atingiu o posto de diretor do Observatório de Ujjain, que era, na época,o maior centro de pesquisas matemáticas e astronômicas da Índia.
Bhaskara obteve grande reconhecimento pelas suas importantes contribuições para a Matemática. Tanto que em 1207, uma instituição educacional foi criada para estudar o seu trabalho. Em um templo indiano, existe uma inscrição medieval na qual se pode ler:
Triunfante e ilustre professor Bhaskara cujas importantes realizações são reverenciadas pelos sábios e eruditos. Um talentoso poeta com fama e mérito religioso. Ele é como a crista de um pavão.
Bhaskara morreu aos 71 anos de idade em Ujjain, Índia, em 1185.
Ele escreveu os livros Lilavat e Vija Ganita que contém problemas sobre equações lineares e quadráticas (equações de segundo grau). É dele a primeira resposta plausível para a divisão por zero. Em seu trabalho “Vija-Ganita” ele afirma que tal quociente é infinito.
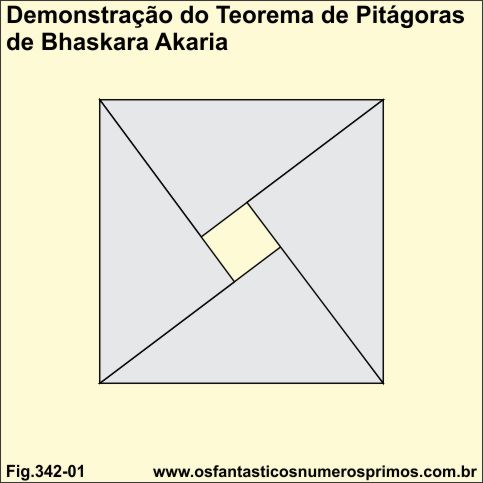
Em sua demonstração do Teorema de Pitágoras, Bhaskara Akaria limitou-se apresentar a construção geométrica da figura 342-01 com a seguinte frase:
"Veja!"...
...deixando para o observador, isto é, para o leitor que decifrasse a construção geométrica de que tinha realizado.
Observação: tanto na construção geométrica de Bhaskara Akaria quanto na do livro Chou Pei Suan Shing e também com triângulos retângulos de 30, 60 e 90 graus há um quadradinho central.
Veja matérias relacionadas, para informações sobre cálculos algébricos e aritméticos.
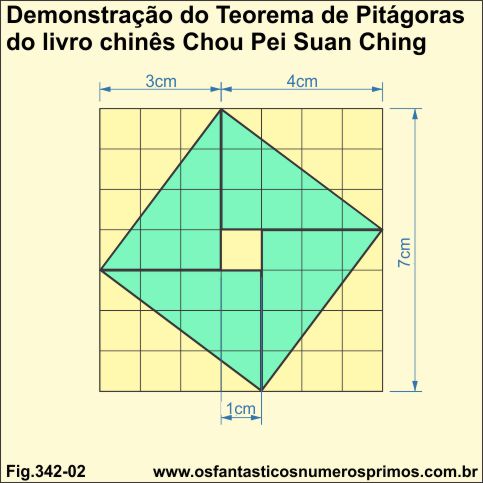
No livro chinês Chou Pei Suan Shing (Clássico Aritmético do Gnomon e os Caminhos Circulares do Céu) há uma das demonstrações mais antigas do Teorema de Pitágoras e que os chineses chamam pelo nome de Teorema Gou-gu.
Os textos do Chou Pei Suan Shing foram escritos no périodo da Dinastia Han (206 a.C. - 222 a.C)
A demonstração do Teorema de Pitágoras aparece sobre um gabarito quadridulado onde estão desenhados 4 retângulos divididos por suas diagonais e cujas divisões formam triângulos retângulos e estes formam um quadrado maior e um outro menor inscritos no gabarito.
O desenho é semelhante ao do matemático Bhaskara Akaria, a diferença é que o observador, consegue visualmente e através de cálculos aritméticos provar a proposição do Teorema de Pitágoras: O quadrado da hipotenusa é igual a soma dos quadrados dos catetos., digamos sem muito esforço..., pois o gabarito quadriculado é um grande auxiliador para tal feito.
Observação: tanto na construção geométrica de Bhaskara Akaria quanto na do livro Chou Pei Suan Shing e também com triângulos retângulos de 30, 60 e 90 graus há um quadradinho central no quadrado inscrito.
Veja matérias relacionadas, para informações sobre cálculos algébricos e aritméticos.
Podemos construir quadrados com figuras de triângulos justapostos a partir de váriadas construções geométricas, o WebSite Os Fantásticos Números Primos está apresentando duas diferentes construções as quais se podem chegar ao mesmo resultado, tanto aritmético quanto algébrico, pois elas apresentam uma característica comum: de que a medida do lado quadradinho central possui a mesma medida unitária dos catetos e da hipotenusa, isto é, 1/5 da hipotenusa, 1/4 do cateto maior e 1/3 do cateto menor.
Neste método, constroi-se um triângulo pitagórico de lados 3-4-5, de forma que a hipotenusa fique alinhada sobre uma reta.
Duplica-se o triângulo, formando-se um retângulo de comprimento 4 e altura 3.
Triplica-se as construções dos retângulos lado a lado, de forma que dois fiquem em posições "horizontais" e 2 em "posições verticais".
Reforçando-se as linhas diagonais dos retângulos e posteriormente dos comprimentos e das alturas da parte interior, formam-se dois quadrados inscritos, um maior e um outro menor na parte central.
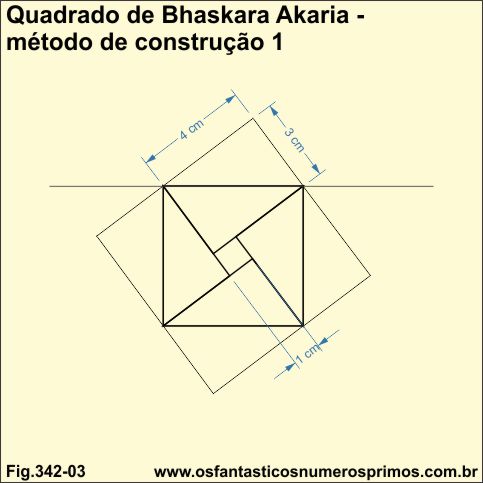
As etapas que se seguem para se construir quadrados inscritos a partir de um triângulo pitágórico 3-4-5 revelam interessantes propriedades geométricas relacionadas aos próprios triângulos pitagóricos.
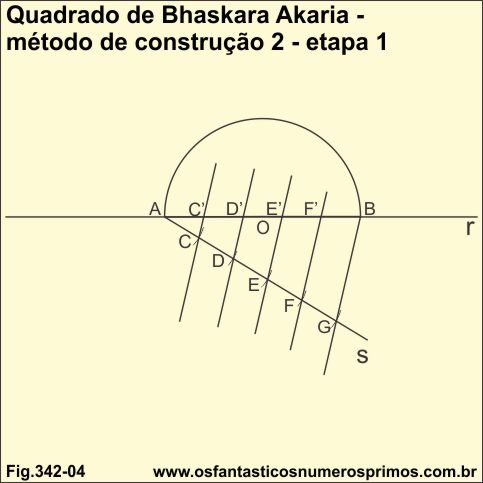
Sobre a reta r, desenha-se um semicircunferência de raio qualquer, obtendo-se os pontos AÔB;
A partir do ponto A , traça-se a reta s de ângulo agudo;
A partir do ponto A, com abertura qualquer do compasso, traça-se o arco AC;
Com a mesma abertura AC, marca-se o pontos: CD, DE, EF FG;
Traça-se um seguimento de reta ligando os pontos BG;
Traçam-se retas paralelas a BG: FF', EE', DD', CC';
Desta forma a hipotenusa fica dividida em 5 partes iguais.
A partir do ponto A, com abertura do compasso até F' (4 unidades), desenha-se uma circunferência de raio 4 (cor azul);
A partir do ponto B, com abertura do compasso até D' (3 unidades), desenha-se uma circunferência de raio 3 (cor vermelho);
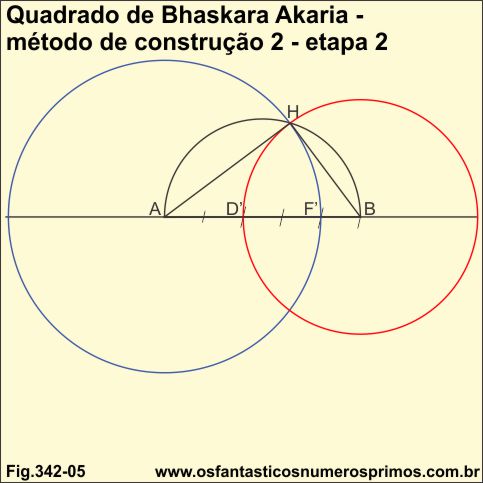
Transporta-se a medida AC', marcando-se o ponto I;
Traçam-se dois arcos de circunferências a partir de C' e I;
A partir do ponto médio A, traça-se a reta perpendicular t;
Com a abertura do compasso AB, marca-se o ponto J;
Com a abertura do compasso AB, marca-se o ponto K;
Unindo-se os pontos A, B, K e J, forma-se um quadrado.
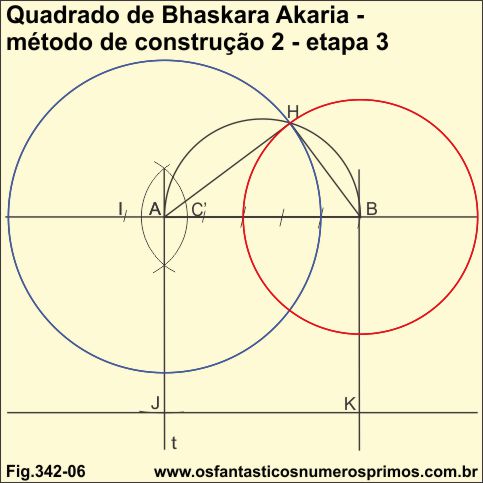
traçam-se retas paralelas a partir de BH, obtendo-se AL e C'K;
traçam-se retas paralelas a partir de AH, obtendo-se BM e NJ;
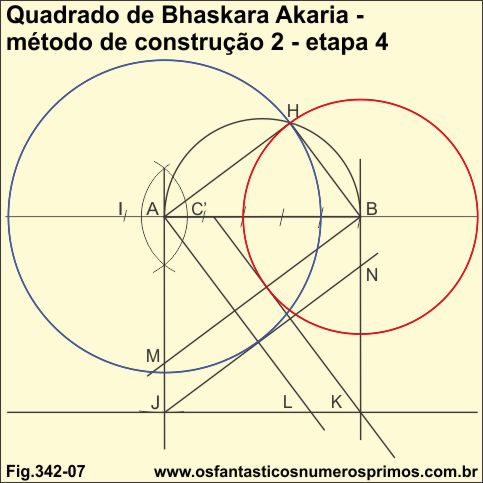
Reforçando-se os seguimentos dos lados do quadrado e dos triângulos retângulos, destaca-se desta forma as figuras geométricas dos dois quadrados; um maior e o outro menor e os 4 triângulos retângulos de lados 3-4-5.
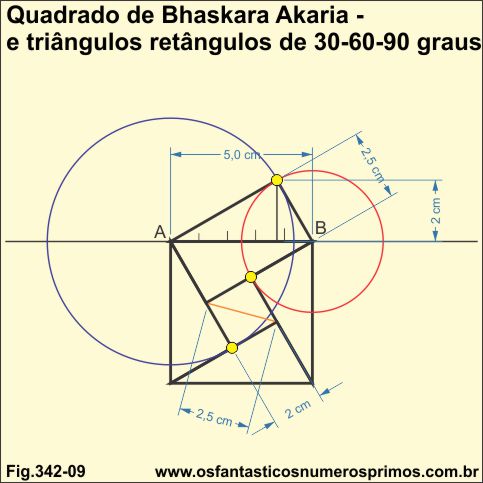
Observação: interessante observar que as circunferências (azul e vermelho) que determinam a altura do triângulo retângulo ABH, intersectam cada uma, um dos vértices do quadradinho central e que a medida dos lados do quadradinho central corresponde a mesma medida unitária dos catetos e da hipotenusa.
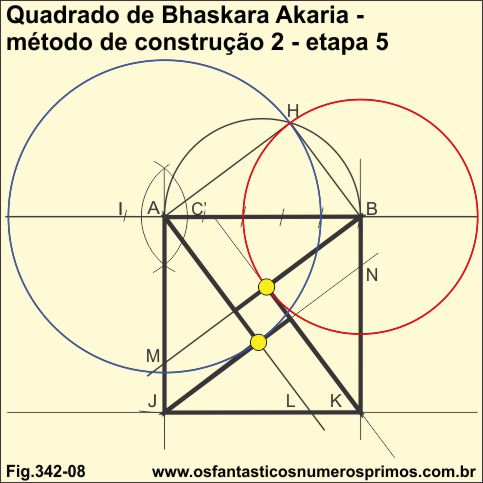
A construção do quadrado de Bhaskara Akaria por meio de triângulos retângulos de 30, 60 e 90 graus aparesentam outras características geométricas:
a) as circunferências que intersectam o ângulo de 90 graus, do triângulo retângulo, também intersectam cada uma, um vértice do quadradinho central;
b) a diagonal do quadradinho (cor laranja) tem a mesma medida do cateto menor;
c) a medida do lado do quadradinho tem a mesma medida da altura do triângulo retângulo.
Autor: Ricardo Silva - maio/2021
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org/wiki/Bhaskara_II
https://en.wikipedia.org/wiki/Zhoubi_Suanjing
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato