


Número Perfeito é um número cuja soma de seus divisores próprios tem como resultado esse número.
6, 28, 496, 8128, 33.550.336, 8.589.869.056, 137.438.691.328 são exemplos de números perfeitos.
2 é um número primo que é par.
2 é o antecessor do número primo 3.
D(2): 1, 2
2 divisores.
Os divisores de 2 somados.
a) 1 + 2 = 3
6 está entre os números primos 5 e 7.
6 é um número perfeito e também triangular, fazendo a decomposiçao em fatores primos tem-se:
| Números Perfeito 6 | |||
|---|---|---|---|
| Fatores Primos | Divisores | ||
| 1 | |||
| 6 | 2 | 2 | |
| 3 | 3 | 3 | 6 |
| 1 | |||
D(6): 1, 2, 3, 6
4 divisores
A soma dos divisores excluído o próprio número:
1 + 2 + 3 = 6
O presente estudo demonstra uma outra propriedade numérica constatada em determinados números naturais e seus divisores.
Somando os divisores equidistantes de um número natural em pares, isto é, de extremos a extremos, as somas apresentam como resultados números primos.
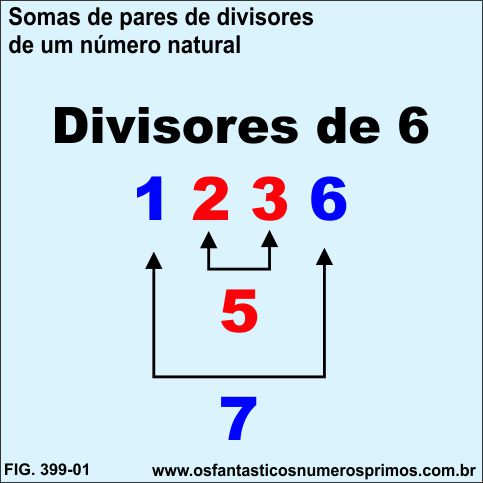
Os divisores de 6 somados em pares, de extremos a extremos, apresentam esta propriedade, vejamos:
a) 1 + 6 = 7
7 é um número primo.
b) 2 + 3 = 5
5 é um número primo.
Alguns números compostos como: semiprimos, oblongos cujas somas de pares de divisores têm como resultados números primos.
10 termina em 0 (zero) e é produto de 2 por 5.
A metade de 10 é 5 e termina em 5.
10 é o antecessor do número primo 11.
D(10): 1, 2, 5, 10
4 divisores.
Os divisores de 10 somados em pares.
a) 1 + 10 = 11
11 é um número primo.
b) 2 + 5 = 7
7 é um número primo.
D(22): 1, 2, 11, 22
4 divisores.
Os divisores de 22 somados em pares.
a) 1 + 22 = 23
23 é um número primo.
b) 2 + 11 = 13
13 é um número primo.
30 termina em 0 (zero) e pode ser obtido através do produto de 3 por 10.
A metade de 30 é 15 e termina em 5.
30 é o antecessor do número primo 31.
D(30): 1, 2, 3, 5, 6, 10, 15, 30
8 divisores.
Os divisores de 30 somados em pares.
a) 1 + 30 = 31
31 é um número primo.
b) 2 + 15 = 17
17 é um número primo.
c) 3 + 10 = 13
13 é um número primo.
d) 5 + 6 = 11
11 é um número primo.
42 é o antecessor do número primo 43.
D(42): 1, 2, 3, 6, 7, 14, 21, 42
8 divisores.
Os divisores de 42 somados em pares.
a) 1 + 42 = 43
b) 2 + 21 = 23
c) 3 + 14 = 17
d) 6 + 7 = 13
Todas as somas são números primos.
70 termina em 0 (zero) e pode ser obtido através do produto de 7 por 10.
A metade de 70 é 35 e termina em 5.
70 é o antecessor do número primo 71.
D(70): 1, 2, 5, 7, 10, 14, 35, 70
8 divisores.
Os divisores de 70 somados em pares.
a) 1 + 70 = 71
b) 2 + 35 = 37
c) 5 + 14 = 19
c) 7 + 10 = 17
Todas as somas são números primos.
78 é o antecessor do número primo 79.
D(78): 1, 2, 3, 6, 13, 26, 39, 78
8 divisores.
Os divisores de 78 somados em pares.
a) 1 + 78 = 79
b) 2 + 39 = 41
c) 3 + 26 = 29
c) 6 + 13 = 19
Todas as somas são números primos.
82 é o antecessor do número primo 83.
D(82): 1, 2, 41, 82
4 divisores.
Os divisores de 82 somados em pares.
a) 1 + 82 = 83
b) 2 + 41 = 43
Todas as somas são números primos.
102 é o antecessor do número primo 103.
D(102): 1, 2, 3, 6, 17, 34, 51, 102
8 divisores.
Os divisores de 102 somados em pares.
a) 1 + 82 = 83
b) 2 + 51 = 53
c) 3 + 34 = 37
d) 6 + 17 = 23
Todas as somas são números primos.
| divisores | soma | primo | |
| 1 | 130 | 131 | sim |
| 2 | 65 | 67 | sim |
| 5 | 26 | 31 | sim |
| 10 | 13 | 23 | sim |
| divisores | soma | primo | |
| 1 | 190 | 191 | sim |
| 2 | 95 | 97 | sim |
| 5 | 38 | 43 | sim |
| 10 | 19 | 29 | sim |
| divisores | soma | primo | |
| 1 | 210 | 211 | sim |
| 2 | 105 | 107 | sim |
| 3 | 70 | 73 | sim |
| 5 | 42 | 47 | sim |
| 6 | 35 | 41 | sim |
| 7 | 30 | 37 | sim |
| 10 | 21 | 31 | sim |
| 14 | 15 | 29 | sim |
| divisores | soma | primo | |
| 1 | 310 | 311 | sim |
| 2 | 155 | 157 | sim |
| 5 | 62 | 67 | sim |
| 10 | 31 | 41 | sim |
| divisores | soma | primo | |
| 1 | 330 | 331 | sim |
| 2 | 165 | 167 | sim |
| 3 | 110 | 113 | sim |
| 5 | 66 | 71 | sim |
| 6 | 55 | 61 | sim |
| 10 | 33 | 43 | sim |
| 11 | 30 | 41 | sim |
| 15 | 22 | 37 | sim |
| divisores | soma | primo | |
| 1 | 358 | 359 | sim |
| 2 | 179 | 181 | sim |
| divisores | soma | primo | |
| 1 | 382 | 383 | sim |
| 2 | 191 | 193 | sim |
| divisores | soma | primo | |
| 1 | 478 | 479 | sim |
| 2 | 239 | 241 | sim |
Os números: 2, 6, 10, 22, 30, 42, 70, 78, 82, 102,... são todos pares, entre eles números semiprimos e oblongos e não apresentam diferença constante entre eles, conforme tabela abaixo, mas as somas de duplas de seus divisores apresentam como resultados números primos.
| Número | diferença |
| 2 | |
| 4 | |
| 6 | |
| 4 | |
| 10 | |
| 12 | |
| 22 | |
| 8 | |
| 30 | |
| 12 | |
| 42 | |
| 8 | |
| 70 | |
| 8 | |
| 78 | |
| 4 | |
| 82 | |
| 4 | |
| 102 | |
| 28 | |
| 130 | |
| 190 | 60 |
| 210 | 20 |
| 310 | 100 |
| 330 | 20 |
| 358 | 28 |
| 382 | 24 |
| 478 | 96 |
| www.osfantasticosnumerosprimos.com.br | |
Autor: Ricardo Silva - setembro /2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://pt.wikipedia.org/

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato