


Escolhendo-se qualquer número de dois algarismos ou mais e subtraindo-se a soma dos seus algarismos, a diferença resultante é um número múltiplo de 3 e de 9.
Escolhendo-se qualquer número de dois algarismos ou mais e subtraindo-se sempre a soma dos algarismos das diferenças resultantes, a diferença final é o número 9.
Propriedade válida para qualquer sequência numérica como: números naturais, números pares, números ímpares, números quadrados perfeitos, etc.
Subtraindo-se a soma dos algarismos de um número composto ou primo de dois ou mais algarismos, o número resultante é divisível tanto por 9 quanto por 3.
Exemplo 1)
88 (número composto)
soma dos algarismos: 8 + 8 =16
88 - 16 = 72
72 é um número divisível tanto por 9 quanto por 3, pois a soma dos seus algarismos é (7 + 2 = 9)
Exemplo 2)
78 (número composto)
soma dos algarismo: 7 + 8 = 15
78 - 15 = 63
63 é um número divisível tanto por 9 quanto por 3, pois a soma dos seus algarismos é (6 +3 = 9)
Exemplo 3)
101 (número primo)
soma dos algarsimos: 1 + 0 + 1 = 2
101 - 2 = 99
99 é um número divisível tanto por 9 quanto por 3, pois a soma dos seus algarismos é (9 +9 = 18)
Subtraindo-se a soma dos algarismos de um número composto de dois ou mais algarismos ou número primo sucessivamente, o número resultante é o número 9.
Exemplo 4)
a)
86 (número composto)
8 + 6 = 14 (soma dos algarismos)
86 - 14 = 72
b)
72 (número composto) - divisível tanto por 9 quanto por 3
7 + 2 = 9 (soma dos algarismos)
72 - 9 = 63
c)
63 (número composto) - divisível tanto por 9 quanto por 3
6 + 3 = 9 (soma dos algarismos)
63 - 9 = 54
d)
54 (número composto) - divisível tanto por 9 quanto por 3
5 + 4 = 9 (soma dos algarismos)
54 - 9 = 45
e)
45 (número composto) - divisível tanto por 9 quanto por 3
4 + 5 = 9 (soma dos algarismos)
45 - 9 = 36
f)
36 (número composto) - divisível tanto por 9 quanto por 3
3 + 6 = 9 (soma dos algarismos)
36 - 9 = 27
g)
27 (número composto) - divisível tanto por 9 quanto por 3
2 + 7 = 9 (soma dos algarismos)
27 - 9 = 18
h)
18 (número composto) - divisível tanto por 9 quanto por 3
1 + 8 = 9 (soma dos algarismos) 18 - 9 = 9
i)
9 é o número resultante
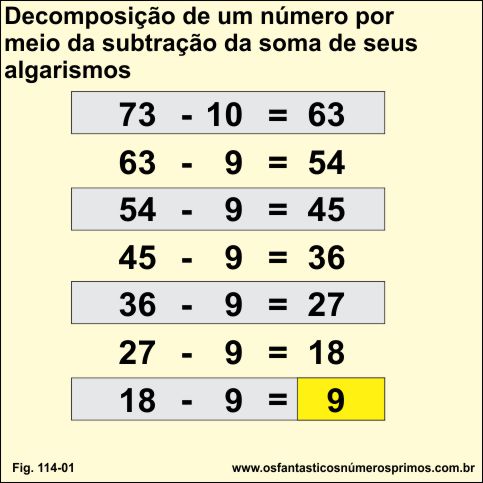
Exemplo 5)
73 (número primo)
O número resultante final é 9.
| Número | Soma dos | diferença | ||
| algarismos | ||||
| 73 | - | 10 | = | 63 |
| 63 | - | 9 | = | 54 |
| 54 | - | 9 | = | 45 |
| 45 | - | 9 | = | 36 |
| 36 | - | 9 | = | 27 |
| 27 | - | 9 | = | 18 |
| 18 | - | 9 | = | 9 |
| www.osfantasticosnumerosprimos.com.br | ||||
Autor: Ricardo Silva - janeiro/2015
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato