


Quadrados Mágicos são dispositivos numéricos formados por matrizes quadriculadas nas quais são dispostas em certa ordem números naturais de 1 a n2 em que a soma de cada uma das linhas, colunas e diagonais apresentam uma mesma soma, denominada de Constante Mágica.
Os Quadrados Mágicos apresentam diversas propriedades algébricas, aritméticas, numéricas, geométricas, etc..., podendo serem construídos com progressões aritméticas, progressões geométricas e também por sequências numéricas constituídas por conjuntos de divisores de números naturais que são produtos de 2 números primos distintos.
Neste estudo são apresentados outras interessantes propriedades relacionadas a Quadrados Mágicos com as quais são possíveis de se contruírem padrões geométricos abstratos.
Quadrado Mágico 4x4 ou de ordem 4 é uma matriz formada por 4 linhas e 4 colunas, perfazendo um total de 16 células onde são dispostos os número naturais de 1 a n2, isto é, os números: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 e 16, neste caso, o quadrado mágico é denominado de Puro, Normal ou Elementar, pois, a partir dele, podem ser construídos outros quadrados mágicos derivados simplesmente somando-se um número constante.
| Quantidade de Combinações | |||
| de Quadrados Mágicos | |||
| Ordem | Quant. | Permutações | Quantidade |
| Células | Quadrados Mágicos | ||
| 3 (3 x 3) | 9 | 362.880 | 8 |
| 4 (4 x 4) | 16 | 20.922.789.888.000 | 880 |
| 5 (5 x 5) | 25 | + de 15 setilhões | 275.305.224 |
| 6 (6 x 6) | 36 | estima-se 1,7 x 10 19 | |
Fonte: Adaptado de Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
Verificando a tabela acima, nota-se o grande empenho do matemático francês Bernard Frénicle de Bessy (1602-1675), em sua Obra - Des Quarrez Magiques Da Academia Royale Des Sciences (1693) - o qual enumerou 880 diferentes quadrados elementares de ordem 4 fazendo o uso de extensos cálculos manuais sem calculadora ou computador.
Harvey Denis Heinz (1930-2013) entusiasta matemático canadense e estudioso de quadrados mágicos publicou em seu WebSite:
http://www.magic-squares.net
no ano de 2010, recálculos dos 880 quadrados mágicos de Bernard Frénicle de Bessy por meio de um Programa de Computador e disse que outros estudiosos de quadrados mágicos também fizeram o mesmo.
Henry Ernest Dudeney (1857-1930) escritor e matemático inglês, especializado em quebra-cabeças lógicos e jogos matemáticos, classificacou os 880 quadrados mágicos de ordem 4 em 12 grupos e que foram publicados na revista The Queen em 15 de janeiro de 1910. Em 1917, a classificação em grupos também foi publicada em Amusements in Mathematics, por Thomas Nelson & Sons, Ltd.
Observe também que estas classificações demandaram um grande empenho em análises criteriosas dos 880 quadrados mágicos para se chegar ao resultado de 12 grupos formados pelos diagramas abaixo.
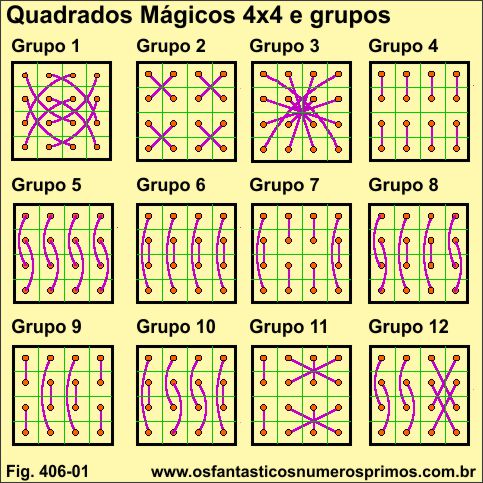
Fonte: adaptado de http://
O método de construção Moschopoulos para construção de Quadrado Mágico 4x4 consiste em formar um quadrado natural com os números de 1 a 16 (figura a) e posteriormente permutar diagonalmente os números das células de mesma cor (figura b), conservando os números das células brancas nas mesmas posições.
Para mais informações, veja abaixo, matérias relacionadas.
Na (figura b), o Quadrado Mágico 4x4 apresenta uma configuração em que duplas de números formam Pares Complementares.
Pares Complementares são duplas de números que apresentam o mesmo resultado de n2 + 1 que é 17.
17 é a metade da Constante Mágica 34.
Exemplos nas células coloridas:
1 + 16 = 17
4 + 13 = 17
6 + 11 = 17
7 + 10 = 17
Somando os números diagonalmente das células brancas também se obtem o número 17.
Sobrepondo o diagrama do Grupo 3 sobre o Quadrado Mágico 4x4 (figura b), visualiza-se facilmente os Pares Complentares.
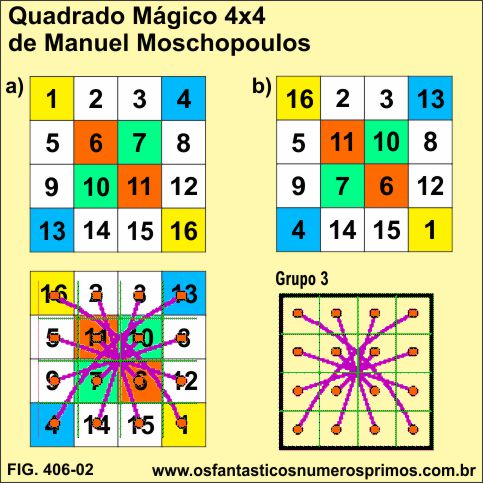
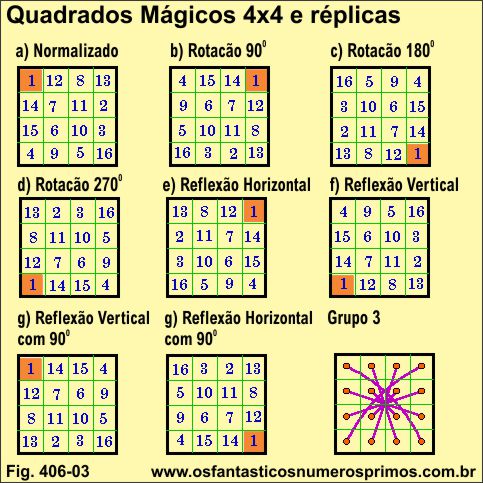
A partir de um Quadrado Mágico 4x4 Normalizado, pode-se obter 7 réplicas por meio de rotações e reflexões.
Quadrado Mágico Normalizado é o quadrado em que o menor número deve estar na primeira célula superior esquerda (figura a) e partindo-se dele, obtêm-se as demais réplicas.
Nos exemplos abaixo, todos os quadrados mágicos se encaixam no Grupo 3 por meio de rotações e reflexões.
Interessante observar que o padrão geométrico formado por pontos e curvas do Grupo 3 se assemelha a fogos de artifício se espalhando pelo ar.
Fonte: adaptado de http://
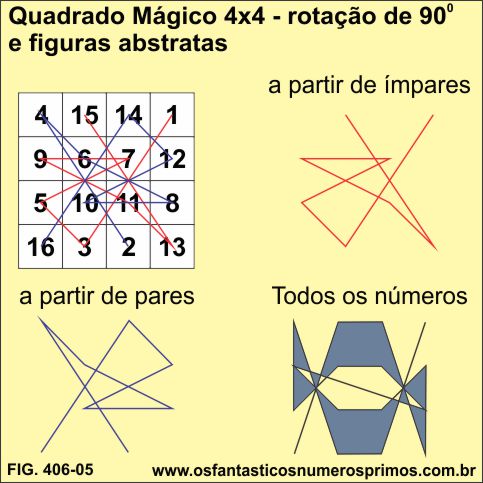
Seguindo-se os números ímpares e traçando-se seguimentos de retas, constroem-se as chamadas Linhas Mágicas com as quais vão surgindo interessantes padrões geométricos, o mesmo acontece, seguindo os números pares.
Seguindo os números sequencialmente, obtem-se figuras geométricas diversas e que posteriormente preenchidas e alternando-se cores, outros padrões abstratos também podem ser formados.
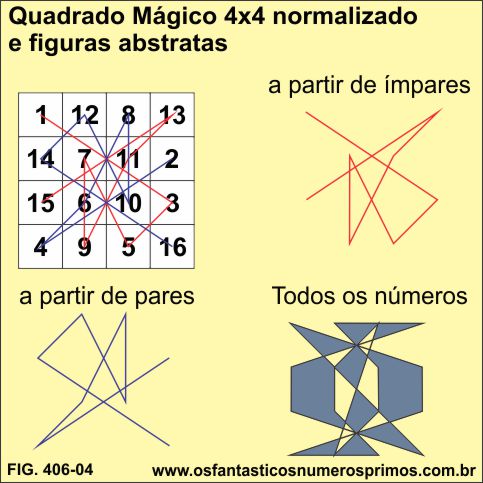
Fonte: adaptado de http://
Fonte: adaptado de http://
Segundo Harvey Denis Heinz (1930-2013) entusiasta matemático canadense, idealizador do WebSite (ano 1999): http://www.magic-squares.net/bibliography.htm, relata que Jim Moran em seu livro The Wonders of Magic Squares, Random House, 1982, se refere a esses padrões abstratos com Sequence Designs.
Autor: Ricardo Silva - dezembro /2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
http://

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato