


Assim como a Trissecção do Ângulo, a Duplicação do Cubo, a Quadratura do Círculo faz parte dos 3 problemas clássicos da geometria grega que ao longo da história vem desafiando a mente humana, isto porque, são problemas geométricos que devem ser resolvidos somente com compasso e régua não graduada.
A Quadratura do Círculo consiste em obter um quadrado de área igual a um círculo dado, problema este que Carl Louis Ferdinand von Lindemann (1852-1939), matemático alemão, declarou ser ímpossível em 1882. Ele provou que Π (pi) é número transcendente.
A Quadratura do Círculo em função da área do próprio círculo e do quadrado, pode até não ter solução, mas a Quadratura do Círculo em função do perímetro do círculo e do quadrado apresenta em sua gênese, interessantes relações matemáticas com diversas outras construções geométricas, como símbolos religiosos, construções arquitetônicas, agroglifos (crop cicles), enfim com a própria natureza.
Os estudos que se seguem tem como referência o artigo: The Key of Life de autoria de Bert Janssen, agrônomo e matemático holandês. Bert Janssen é escritor, contador de histórias, palestrante e estudioso de geometria sagrada e crop cicles (agroglifos).
As diferenças entre áreas e perímetros de quadrado circunscrito numa círcunferência são bem significativos.
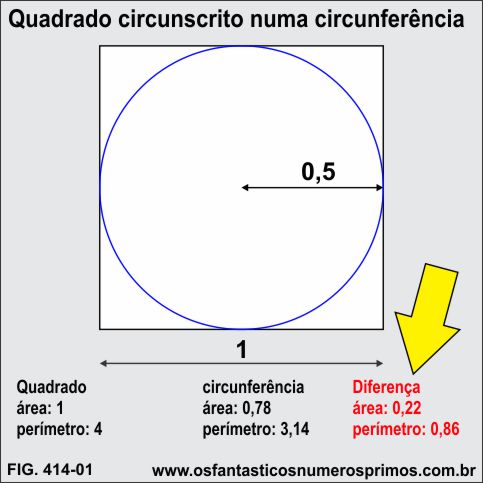
As diferenças entre áreas e perímetros de quadrado inscrito numa círcunferência são bem significativos.
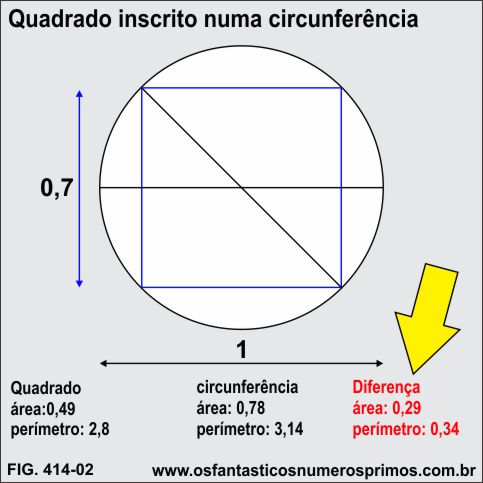
A diferença entre o perímetro do círculo e do quadrado na Quadratura do Círculo em função de áreas é significativa.
A diferença entre a área do círculo e do quadrado na Quadratura do Círculo em função de áreas, podemos dizer, que é quase imperceptível, bastante interessante, diferença de 1 centésimo.
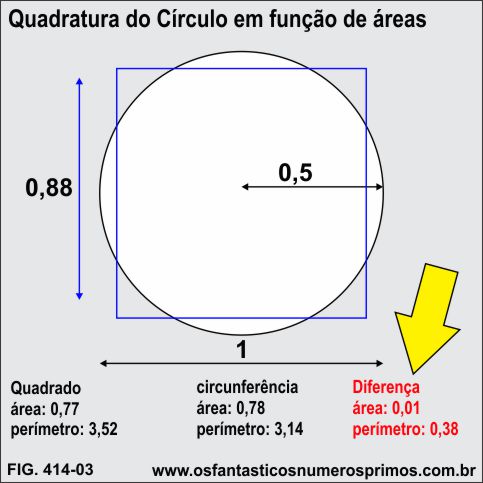
A diferença entre a área do círculo e do quadrado na Quadratura do Círculo em função de perímentos é bem significativa.
A diferença entre o perímetro do círculo e do quadrado na Quadratura do Círculo em função de perímentos, podemos dizer, também, que é quase imperceptível, bastante interessante, diferença de 2 centésimos.
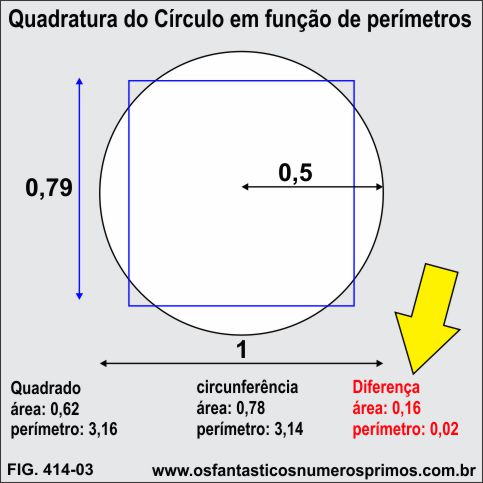
Se a Terra girasse em torno do seu eixo perpendicularmente ao executar o movimento de translação, os raios solares estariam sempre a pino fazendo com que dias e noites tivessem sempre a mesma duração, mas não é o que acontece, a Terra gira com uma inclinação de 23,5 graus. E esta inclinação de 23,5 graus é o que ocasiona as estações do ano fazendo com que se alternem nos hemisférios norte e sul, as épocas de verão, outono, inverno e primavera.
O evento do Sol a pino acontece com maior intensidade no Solstício (Solstício significa Sol parado; em latim: solstitium):
de verão (dezembro) - hemisfério sul - Trópico de Capricórnio;
de verão (junho) - hemisfério norte - Trópico de Cancer.
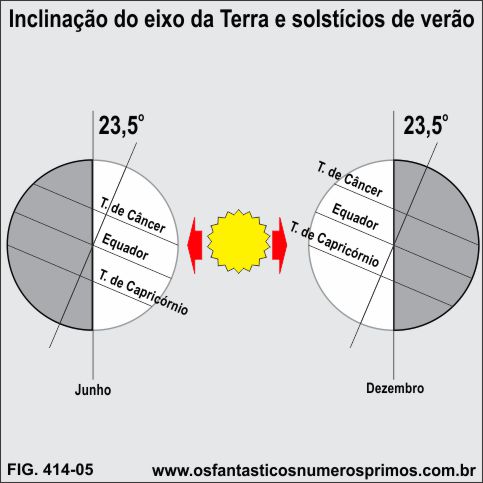
Fonte: adaptado de Tamdjian, James Onig. Geografia geral e do Brasil: estudos para compreensão do espaço: ensino médio/volume único James & Mendes. - São Paulo: FTD. 2005.
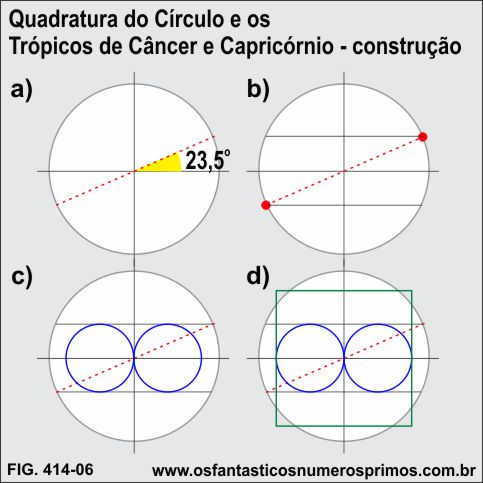
Para se construir a Quadratura do Círculo em função de perímetros em que há relações geométricas com os Trópicos de Câncer e Capricórnio, procedemos com as seguintes etapas:
a) constroem-se duas retas perpendiculares e partir de suas intersecções numa circunferência e posteriormente um diâmetro com 23,5 graus (segmento vermelho pontilhado);
b) nas intersecções da circunferência com o diâmetro (pontilhado), traçam-se cordas que representam respectivamente os Trópicos de Câncer e Capricórnio;
c) controem-se duas circunferências (cor azul) que tangenciem as cordas (Trópicos) e também o centro da circunferência maior;
d) construir um quadrado (cor verde) cuja a medida do lado seja a soma dos diâmetros das duas circunferências menores (cor azul) e seu centro na intersecção das retas perpendiculares.
Você visitante, há de concordar comigo, é simplesmente fantástico!!!, maravilhoso!!!, essas conexões geométricas da Quadratura do Círculo em função dos perímetros envolvendo a Terra e os Trópricos de Câncer e de Capricórnio e principalmente com o eixo de inclinação de 23,5 graus.
Assim como, a partir de uma circunfêrencia, podemos construir polígonos regulares e as mais diversas estruturas geométricas e o mesmo podemos dizer da Vesica Piscis e da Mandorla, tem-se também a Quadratura do Círculo.
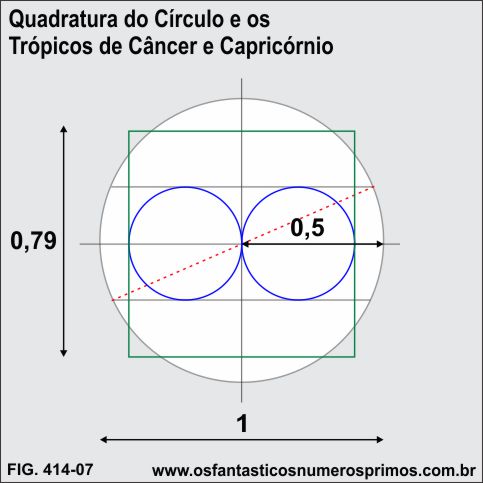
Fonte: adaptado de
https://www.cropcirclesandmore.com
Autor: Ricardo Silva - dezembro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
TAMDJIAN, James Onig. Geografia geral e do Brasil: estudos para compreensão do espaço: ensino médio/volume único James & Mendes. - São Paulo: FTD. 2005.
Indrodução à Astronomía e Astrofísica. INPE - Instituto Nacional de Pesquisas Espaciais, São José dos Campos 2018
https://www.cropcirclesandmore.com/
https://pt.wikipedia.org/wiki/
https://pt.wikipedia.org/

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato