


O pentágono é um polígono regular de 5 lados congruentes e também com 5 ângulos congruentes, por ser regular, pode ser inscrito e circunscrito numa circunferência.
O pentágono possui interessantes propriedades geométricas e numéricas, eis algumas delas:
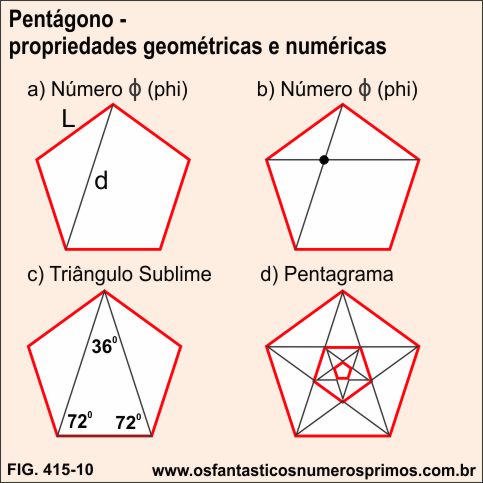
a) a razão entre a medida da diagonal com seu lado tem como resultado o número Φ (phi), isto é, o Número de Ouro;
b) a intersecção de duas diagonais, divide a diagonal em média e extrema razão, conhecida também Secção Áurea cujo resultado é o número Φ (phi), isto é o Número de Ouro;
c) partindo-se de um dos vértices e traçando-se duas diagonais até os ângulos de lados opostos, obtem-se o Triângulo Sublime, triângulo este que apresenta também propriedades relacionadas ao número Φ (phi);
d) traçando-se todas as diagonais do pentágono, obtem-se uma estrela de cinco pontas, denominada de pentagrama cujo em seu interior forma-se um outro pentágono em sentido oposto. Continuando esse processo, mais e mais pentagramas e pentágonos são obtidos infinitamente.
O pentágono por possuir essas propriedades geométricas e poder gerar o pentagrama, eram figuras veneradas pelos Pitagóricos que as utilizavam como símbolo de sua escola.
Acredita-se que o descobrimento de número incomensurável (número irracional) tenha surgido do pentágono e não do quadrado.
Assim como símbolo utilizado pelo Pitagóricos, o pentagrama aparece também associado a diversas outras culturas, religiões, misticismo, magia, etc...
Os estudos a seguir demonstram diversos métodos de construções da figura geométrica do pentágono e também a contrução do pentágono a partir da Quadratura do Círculo em função de perímetros do círculo e do quadrado.
Tendo-se como base retas perpendiculares e a circunferência de raio qualquer, seguindo-se as etapas numeradas, constrói-se um pentágono.
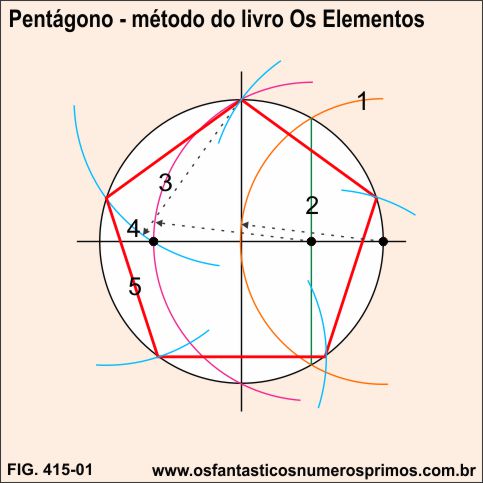
Fonte: adaptado da Apostila Senai - SP - SE - Desenho Mec III
Tendo-se como base retas perpendiculares e a circunferência de raio qualquer, seguindo-se as etapas numeradas, dividi-se a circunferência em 10 partes e posteriormente constrói-se um pentágono.
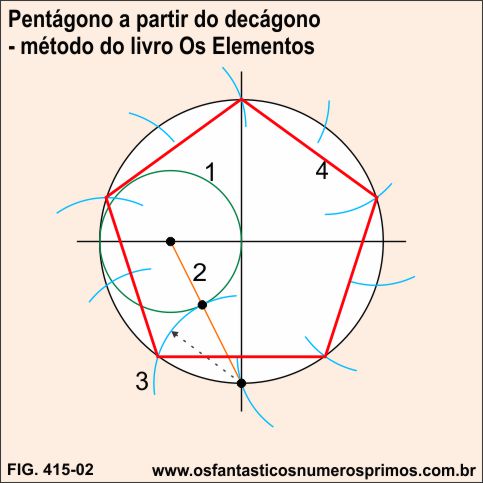
Fonte: adaptado de SILVA, Alex Cristophe Cruz da. A Construção do Pentágono Regular segundo Euclides
Tendo-se como base retas perpendiculares e a Vesica Piscis, seguindo-se as etapas, constrói-se um pentágono.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionadas abaixo.

Fonte: adaptado de SILVA, Alex Cristophe Cruz da. A Construção do Pentágono Regular segundo Euclides
Tendo-se como base retas perpendiculares e a Mandorla, seguindo-se as etapas, constrói-se um pentágono.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionadas abaixo.
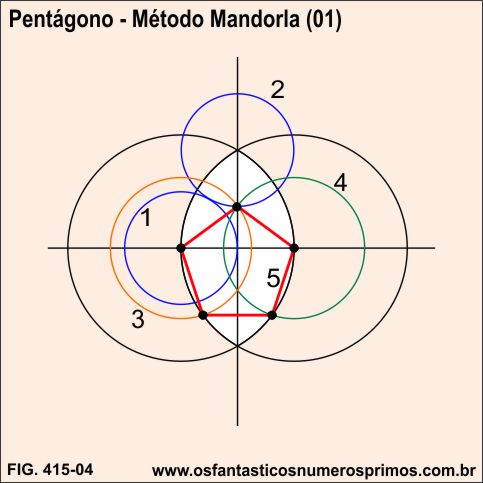
Fonte: adaptado de SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces
Tendo-se como base retas perpendiculares e a Mandorla, seguindo-se as etapas, constrói-se um pentágono.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionadas abaixo.
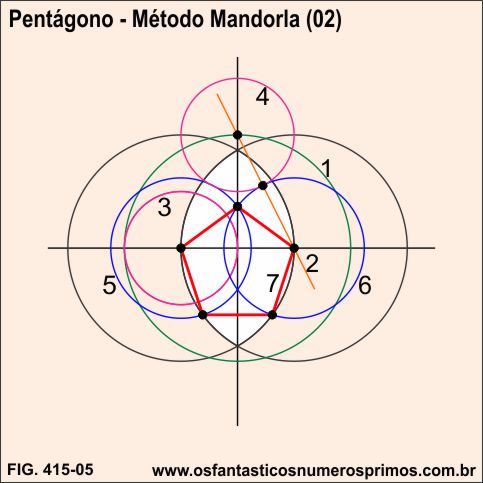
Fonte: adaptado de SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces
Tendo-se como base retas perpendiculares e a Vesica Piscis, seguindo-se as etapas, constrói-se um pentágono.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionadas abaixo.

Fonte: adaptado de SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces
Tendo-se como base retas perpendiculares e a Vesica Piscis, seguindo-se as etapas, constrói-se um pentágono.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionadas abaixo.
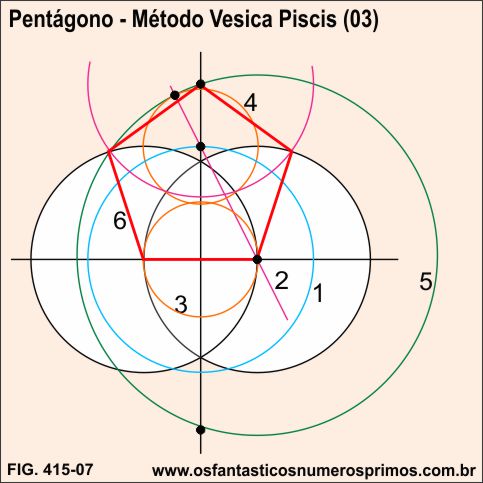
Fonte: adaptado de SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces
Tendo-se como base retas perpendiculares e a Vesica Piscis, seguindo-se as etapas, constrói-se um pentágono.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionas abaixo.
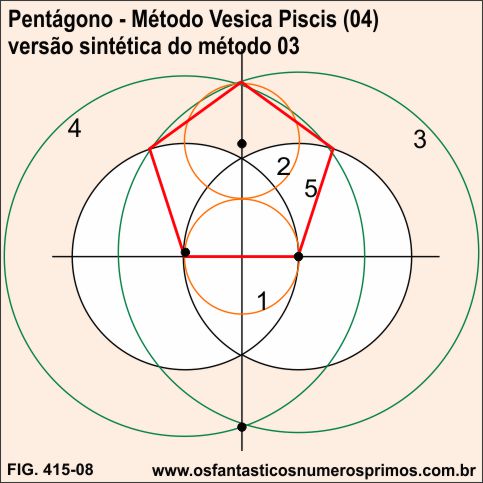
Interessante observar que no Método Rinaldini para construções de polígonos estão explícitos a Vesica Piscis e a Mandorla.
Para mais informações sobre a Vesica Piscis e a Mandorla, veja matérias relacionas abaixo.
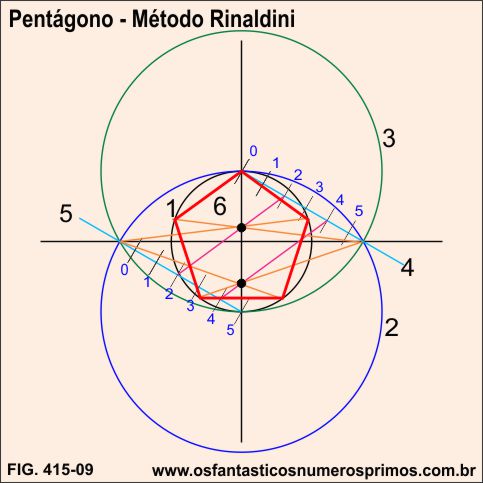
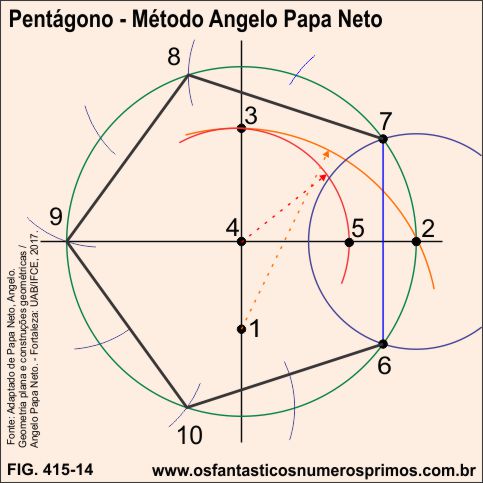
A partir de retas perpendiculares e uma circunferência:
a) centro no ponto médio 1, traçar um arco de abertura do ponto 2 até o ponto 3;
b) centro no ponto 4, traçar um arco do ponto 3 até o ponto 5
c) centro no ponto 2, abertura 4-5, traçar um circunferência, originando os ponto 6-7;
d) o seguimento 6-7 é um dos lados do pentágono;
e) traçar arcos de circunferências e unir com seguimentos os pontos: 7-8-9-10-6, desta forma, se tem um pentágono.
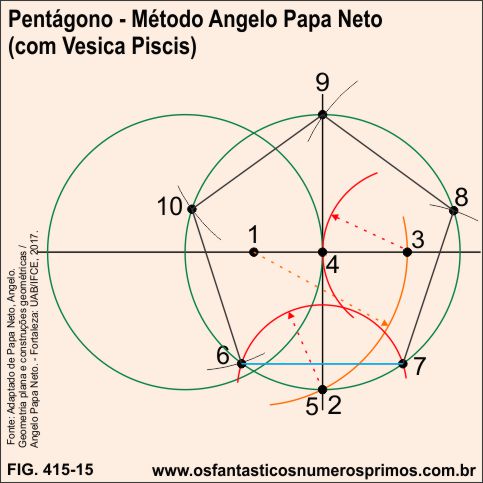
Tendo-se como base retas perpendiculares e a Vesica Piscis, seguindo-se as etapas, constrói-se um pentágono por meio do Método Angelo Papa Neto com a Vesica Piscis.
A Quadratura do Círculo é um dos 3 famosos problemas geométricos gregos que consiste em contruir um quadrado de mesma área de um círculo dado com apenas compasso e régua não graduada.
Mesmo a Quadratura do Círculo tendo aproximações em relação às áreas do círculo e do quadrado e em relação aos perímentros do círculo e do quadrado, ela apresenta propriedades geométricas e matemáticas notáveis.
Com a Quadratura do Círculo pode-se construir o pentágono e consequemente o pentagrama.
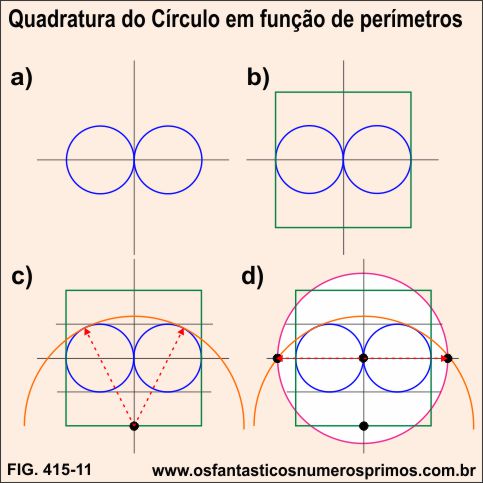
a) constrói-se duas retas perpendiculares e duas circunferências (cor azul escuro) de mesmo raio (de medida qualquer) com centros no seguimento horizontal tangente uma à outra pelo seguimento vertical;
b) constrói-se um quadrado (cor verde) cuja medida do lado seja a soma dos diâmetros das duas circunferências (cor azul escuro) e centralizado nas retas perpendiculares;
c) com centro na intersecção do seguimento vertical com o ponto médio da base do quadrado, traça-se uma semicircunferência (cor laranja) que tangenciem as duas circunferências (cor azul escuro);
d) com centro na intersecção das retas perpendiculares e raio na intersecção da reta horizontal com a semicircunferência, traça-se a circunferência (cor lilás), obtendo-se assim a Quadratura do Círculo em função dos perímetros do círculo e do quadrado.
Fonte: adaptado de
https://www.cropcirclesandmore.com
Com a construção da Quadratura do Círculo em função de perímetros:
a) inscreve-se uma circunferência (cor marrom) no quadrado (cor verde);
b) centro na intersecção base do quadrado com a reta vertical, traça-se uma circunferência (cor azul) que tangenciem as circunferências (cor azul escuro);
c) unindo os pontos de intersecções (cor amarelo) forma-se um pentágono na Quadratura do Círculo.

Fonte: adaptado de
https://www.cropcirclesandmore.com
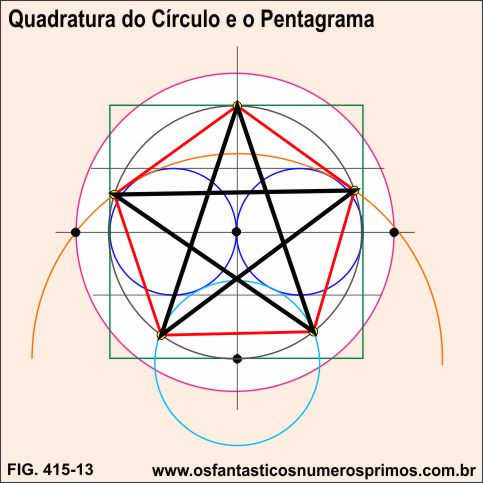
Unindo-se as diagonais do pentágono, obtem-se o Pentagrama a partir da Quadratura do Círculo em função de perímetros.
Fonte: adaptado de
https://www.cropcirclesandmore.com
Autor: Ricardo Silva - dezembro /2022
PAPA NETO , Angelo. Geometria plana e construções geométricas / Angelo Papa Neto. - Fortaleza: UAB/IFCE, 2017.
SILVA, Alex Cristophe Cruz da. A Construção do Pentágono Regular segundo Euclides. Dissertação apresentada ao Corpo Docente do Mestrado Pro fissional em Matemática em Rede Nacional PROFMAT CCEN-UFPB, como requisito parcial para obtenção do título de Mestre em Matemática. Julho/2013, João Pessoa - PB
SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces - As possilibilidades de construção - Dissertação de Mestrado. Universidade de Lisboa - Faculdade de Belas Artes, 2013.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://www.cropcirclesandmore.com

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato