


Um modelo matemático clássico e bastante intuitivo de se demonstrar o Teorema de Pitágoras é construir um triângulo retângulo de lados 3, 4 e 5 de medidas unitárias e posteriormente construir sobre estes mesmos lados quadrados quadriculados cujas áreas são cada lado do triângulo ao quadrado conforme figura a seguir:
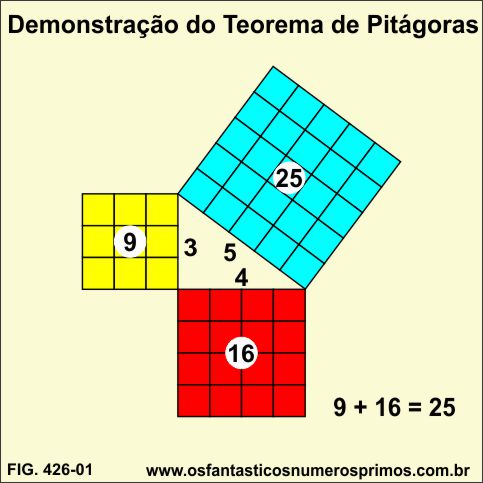
Somando-se os 9 quadradinhos amarelo como os 16 quadradinhos vermelho, o resultado é os 25 quadradinhos azul, provando se assim que:
A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa
ou O quadrado da hipotenusa é igual a soma dos quadrados dos catetos
a2 = b2 + c2
Atualmente existem muitas demonstrações do Teorema de Pitágoras e neste momento alguém pode até estar realizando uma nova demonstração.
O professor de matemática estadunidense Elisha Scott Loomis catalogou em sua Obra - The Pythagorean Proposition (1940 - segunda edição) - mais de 500 demonstrações do Teorema de Pitágoras, entre elas, 5 demonstrações de Quadrados Mágicos Pitagóricos produzidos entre os anos de 1898 a 1924 (data da primeira edição do livro).
Aqui no WebSite Os Fantásticos Números Primos também são apresentadas novas demonstrações do Teorema de Pitágoras. (veja abaixo, matérias relacionadas)
Outra demonstração muito interessante do Teorema de Pitágoras foi apresentado pelo Professor Eduardo Wagner no PAPMEM (Programa de Aperfeiçoamento para Professores de Matemática do Ensino Médio) - julho 2006.
Dois amigos matemáticos, João e José estão em uma Pizzaria, olham o cardápio, analisam os preços e resolvem pedir pizzas.
João diz estar com bastante fome, pede:
1 pizza grande - preço R$ 27,00
José diz estar com muito mais fome, pede:
1 pizza média - preço R$ 17,00
1 pizza brotinho - preço R$ 10,00
A pergunta que se faz é a seguinte: Quem comerá mais pizza?
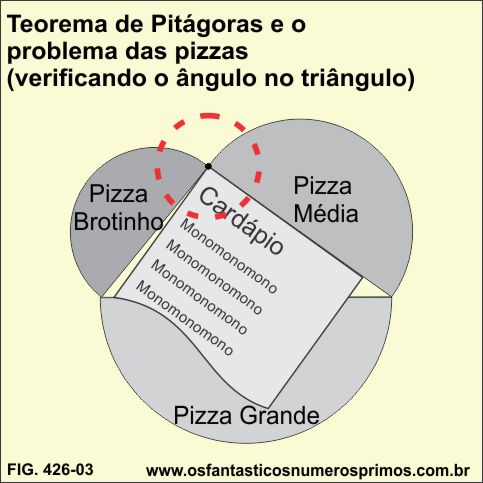
Os professores, então, decidem cortar as pizzas ao meio e constroem o seguinte modelo matemático:

Pegou-se o Cardápio, alinhou-o com o lado médio na junção com o lado menor e verificou-se que o ângulo não era de 90 graus (ângulo reto) e sim um ângulo maior que 90 graus, formando um triângulo obtusângulo.
Portanto, o Professor João é quem mais pizza saboreará.
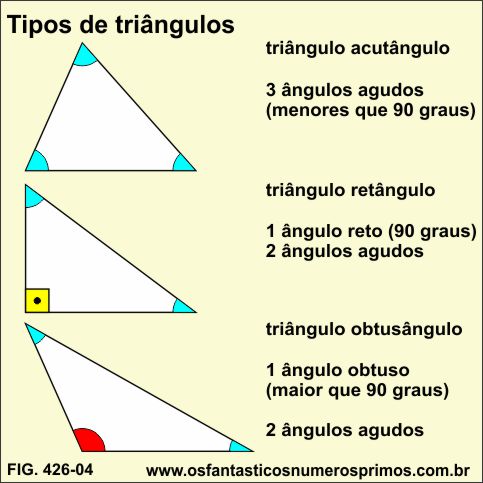
Quanto aos ângulos, o triângulo pode ser classificado como:
Triângulo acutângulo - possui três ângulos internos agudos;
Triângulo retângulo - possui um ângulo reto e dois agudos;
Triângulo obtusângulo - possui um ângulo interno obtuso e dois agudos.
Em todo triângulo, o maior lado se encontra oposto ao maior ângulo.
No problema das pizzas, a pizza grande (a sua metade) se encontra oposto ao maior ângulo, que neste caso, é um ângulo maior que 90 graus, formando um triângulo obtusângulo.
Sabemos que a2 = b2 + c2 é uma relação exclusiva para triângulo retângulo, portanto:
se a2 > (maior que) b2 + c2 tem-se um obtusângulo,
se a2 < (menor que) b2 + c2 tem-se um acutângulo.
Por exemplo, qual é tipo de triângulo cujos lados medem: 5cm, 3cm e 7cm.
a = 7 (lado maior)
b = 5 (lado "médio")
c = 3 (lado menor)
a2 = 49
b2 = 25
c2 = 9
como 49 > (maior que) 25 + 9
como 49 > (maior que) 34
então, se a2 > (maior que) b2 + c2 , o triângulo é obtusângulo.
A título de curiosidade, o WebSite Forumdepizzas.net, idealizado pelo Cheff Hassin Ghannam, respondendo dúvidas sobre pesos e medidas de pizzas, publicou, em 2016, uma tabela consultiva com características de como deve ser o aspecto final da massa na fabricação de pizza conforme seu tipo e diâmetro.
| Pizza | Tamanho do | ||
| disco / | disco | disco com | |
| diâmetro | sem borda | borda | |
| (cm) | (gramas) | (gramas) | |
| Colegial | 20 | 105 | 120 |
| Brotinho | 22 | 140 | 160 |
| Individual | 25 | 160 | 180 |
| Média | 30 | 230 | 260 |
| Familiar | 35 | 330 | 380 |
| Grande | 40 | 431 | 495 |
| Super-grande | 45 | 454 | 625 |
| Gigante | 50 | 673 | 775 |
Fonte: adaptado de www.forumdepizzas.net
Autor: Ricardo Silva - abril/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato