


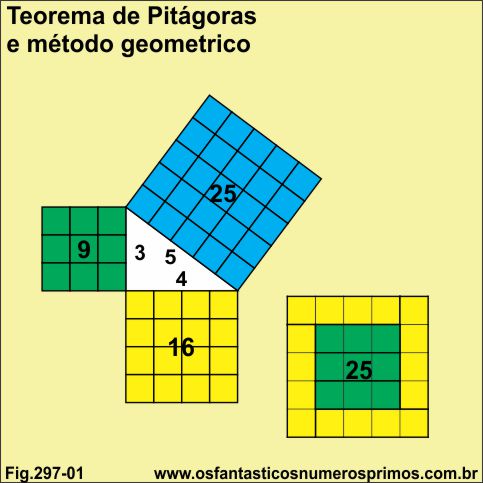
Um dos modelos geométricos clássicos, divulgados em diversos livros, publicações, teses de mestrados, TCCs (Trabalho de Conclusão de Curso), meios digitais, etc., para se comprovar o Teorema de Pitágoras a²=b²+c² é através de figuras geométricas semelhantes como no exemplo: um triângulo retângulo no qual são construídos quadrados quadriculados sobre a hipotenusa e catetos.
Somando os quadradinhos verde mais os quadradinhos amarelo, o resultado são os quadradinhos azul.
9 + 16 = 25
No livro Pythagorean Proposition, Classics in Mathematics Education Serie do professor estadunidense Elisha Scott Loomis, cuja segunda edição foi lançada em 1940, encontra-se uma coletânea de 370 demonstrações do Teorema de Pitágoras entre elas: 109 demonstrações algébricas e 255 demonstrações geométricas.
Outro livro que também aborda demonstrações do Teorema de Pitágoras: Pythagorean Theorem – Crowl Jewl of Mathematics, edição de 2008, do engenheiro estadunidense John C. Sparks.
George Pólya (1887-1985), matemático húngaro, usou o Teorema de Pitágoras para comprovar que esta importante relação entre áreas vale para quaisquer figuras semelhantes desenhadas sobre a hipotenusa e sobre os catetos de um triângulo retângulo.

Fonte: SANTOS, Ana Maria Quaresma dos; SANTOS, Fábio Henrique da Costa; OLIVEIRA, Reinaldo Melo de. Teorema de Pitágoras: Demostrações - Trabalho de Conclusão de Curso - Universidade Federal do Amapá - Macapá/AP, 2015.

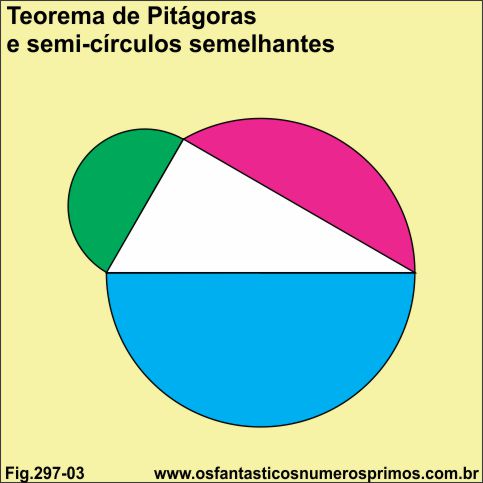
Esta demonstração do Teorema de Pitágoras surgiu a partir de estudos realizados com triângulos retângulos inscritos em semicircunferências, circunferências concêntricas, Vesica Piscis e Mandorla, estudos estes que estão publicados aqui no WebSite Os Fantásticos Números Primos.
Veja matérias relacionadas, para mais informações.
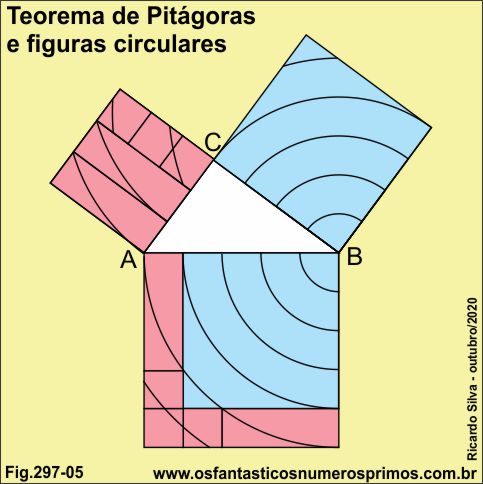
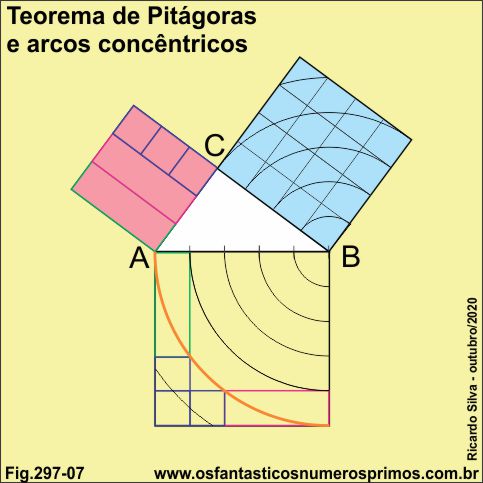
A partir do ponto B, traçou-se arcos de circunferências concêntricos e equidistantes nas áreas dos quadrados do cateto maior e da hipotenusa.
Inclinando o quadrado do cateto maior para a esquerda até a hipotenusa e posteriormente fazendo um giro de 180 graus, o grafismo, isto é, o desenho do cateto maior coincidirá com o desenho sobre o quadrado da hipotenusa.
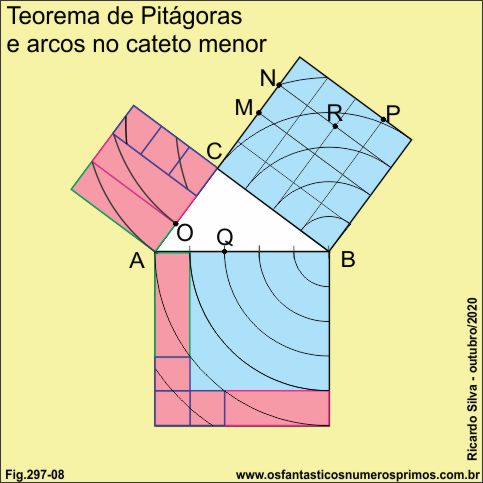
O quadrado do cateto menor foi dividido em quatro áreas, dois retângulos e três quadradinhos.
No quadrado da hipotenusa, um retângulo foi colocado no canto esquerdo superior, o outro no canto direito inferior e os quadradinhos formando uma letra L "éle" no canto esquerdo inferior.
Observação importante:
O quinto arco de circunferência toca os vértices opostos dos retângulos como se fossem linhas diagonais.
O quinto arco de circunferência toca exatamente as larguras e os comprimentos dos retângulos, deixando "sobrar" os três quadradinhos.
E o mais interessante nesta construção geométrica é que a partir de pontos notáveis como ponto médio, ponto de 1/4 dos lados do quadrado do cateto maior determina-se os arcos de circunferências nos retângulos e quadradinhos do quadrado do cateto menor.
Constrói-se um triângulo retângulo de lados 3-4-5 e os quadrados dos catetos e da hipotenusa em seus respectivos lados.
Dividi-se a hipotenusa em 5 unidades.
Dividi-se a área do cateto maior em 16 quadrados.
Dividi-se a área do cateto menor em 2 retângulos e 3 quadrados.
No quadrado da hipotenusa aloca-se os 2 retângulos e os 3 quadrados referente a área do cateto menor.
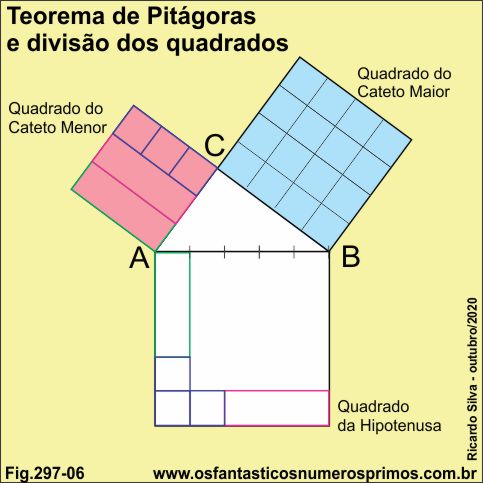
Com centro em B traça-se arcos de circunferências a partir das divisões da hipotenusa no quadrado do cateto maior e no quadrado da hipotenusa.
O quinto arco de circunferência (cor laranja) intersecta os vértices do dois retângulos como se fossem diagonais.
Com centro em M e abertura em A, trace-se o arco no primeiro retângulo.
Com centro em N e abertura em O, traça-se o arco no segundo retângulo.
Com centro em P e abertura em Q, traça-se o arco nos dois pequenos quadrados simultaneamente.
Com centro em R e mesma abertura de PQ, traça-se o arco no terceiro pequeno quadrado.
Autor: Ricardo Silva - outubro/2020
LOOMIS, Elisha Scott. The Pythagorean Propositions - Classics in Mathematics Education Serie - by The National Council of Teachers of Mathematics, Inc. - 1968
SANTOS, Ana Maria Quaresma dos; SANTOS, Fábio Henrique da Costa; OLIVEIRA, Reinaldo Melo de. Teorema de Pitágoras: Demostrações - Trabalho de Conclusão de Curso - Universidade Federal do Amapá - Macapá/AP, 2015.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
SPARKS, John C. Pythagorean Theorem – Crowl Jewl of Mathematics, edição digital de 2008.
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato