


O Teorema de Pitágoras a² = b² + c² prima pela simplicidade, isto é, diferentemente de outras fórmulas e equaçôes é uma equação de fácil entendimento na sua utilização mais trivial para se obter as medidas dos lados de um triângulo retângulo, tendo duas das medidas dos seus lados é possível se obter a medida do terceiro lado.
Uma das propriedades relacionadas aos termos da fórmulas a² = b² + c² é que podem ser gerados infinitos conjuntos de três números inteiros denominados de Ternos Pitágoricos que também se relacionam com cada um dos lados de um triângulo retângulo.
O Teorema de Pitágoras possui aplicação em diversas áreas do conhecimento humano como astronômia, engenharia, fisíca, geometria, trigonometria, matemática, entre outras, etc.
Ao longo da História, tantos matemáticos como entusiastas matemáticos têm apresentados demonstrações do Teorema de Pitágoras que primam pela criatividade e engenhosidade.
O Professor estadunidense Elisha Escott Loomis catalogou mais de 370 demonstrações do Teorema de Pitágoras e que estão publicados em seu livro The Phitagorean Proposition, publicada em 1940, entre as demonstrações algébricas e geometricas estão exemplos de Quadrados Mágicos Pitagóricos, isto é, quadrados mágicos sobre os lados de triângulos retângulos contruídos com sequência de múltiplos de termos ternos pitagóricos.
Veja matérias relacionadas, para mais informações.
Outro livro que também aborda demonstrações do Teorema de Pitágoras é Pythagorean Theorem – Crowl Jewl of Mathematics, edição de 2008, do engenheiro estadunidense John C. Sparks. Há um estudo sistemático com sobreposição, dissecção, translação de figuras geométricas de como pode ter surgido a primeira demonstração do Teorema de Pitágoras.
No livro digital O Triângulo Retângulo - Novas fórmulas algébricas e aritméticas de cálculos são apresentados novos métodos e algoritmos para se calcular lados de triângulos retângulos, diagonais de quadrados e retângulos (download gratuito aqui no WebSite).
Abaixo alguns exemplos clássicos de demonstrações do Teorema de Pitágoras por matemáticos e entusiastas matemáticos.
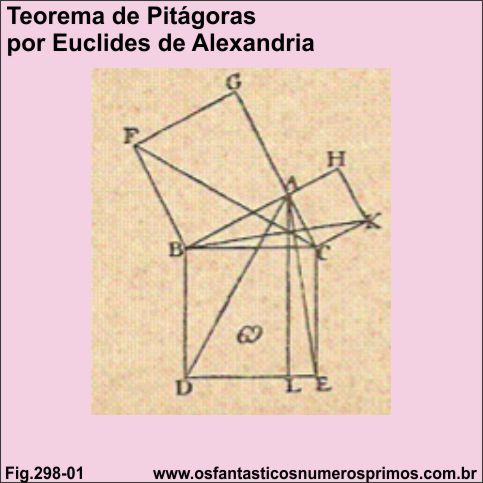
Fonte: EUCLIDES, Elementos de Geometria dos seis primeiros livros do undécimo e duodécimo da versão latina de Frederico Commandino. Edições Cultura, São Paulo, 1944
Zhoubi Suanjing
"Zhou" refere-se à antiga dinastia Zhou (1046–256 aC).
"Bi" significa coxa e, de acordo com o livro, refere-se ao gnômon do relógio de sol.
"Suan Jing" "clássico da aritmética".
Chou Pi Suan Ching - transliteração.

Fonte: LOOMIS, Elisha Scott. The Pythagorean Propositions - Classics in Mathematics Education Serie - by The National Council of Teachers of Mathematics, Inc. - 1968
Diagrama adicionado por Zhao Shuang (século III dC) ao Zhoubi Suanjing (Chou Pei Suan Ching) que pode ser usado para provar o Teorema de Pitágoras.

Fonte:https://pt.wikipedia.org/wiki/
Bhaskara Akaria (1114-1185) matemático indiano, também conhecido como Bhaskaracharya.
Nota: Não confudir com o também matemático indiano Bhaskara I que viveu no século VI.
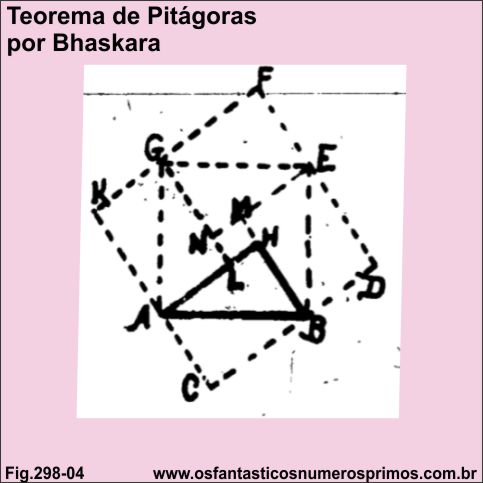
Fonte: LOOMIS, Elisha Scott. The Pythagorean Propositions - Classics in Mathematics Education Serie - by The National Council of Teachers of Mathematics, Inc. - 1968
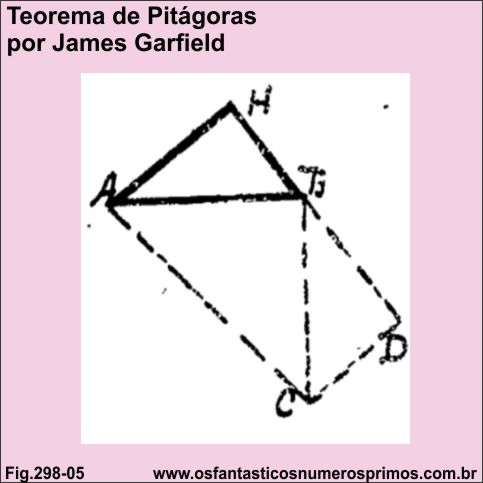
Fonte: LOOMIS, Elisha Scott. The Pythagorean Propositions - Classics in Mathematics Education Serie - by The National Council of Teachers of Mathematics, Inc. - 1968

Fonte: By Henry Perigal - Archives of the Mathematical Association Public Domain
https://commons.wikimedia.org
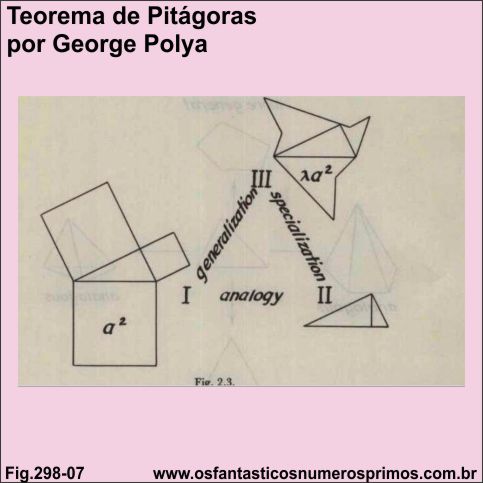
Fonte: POLYA, George, Induction And Analogy In Mathematics 1
https://archive.org/details/
Interessante destacar que nos livros The Phitagorean Proposition e Pythagorean Theorem – Crowl Jewl of Mathematics são apresentados em suas totalidades demonstrações com figuras geométricas retilíneas, não há demonstrações com figuras geométricas mistas, isto é, figuras com contornos retos e curvos.
A demonstração do Teorema de Pitágoras que se segue surgiu de estudos com triângulos retângulos inscritos em semicircunferências, circunferências concêntricas, Vesica Piscis e Mandorla, estudos estes que estão publicados aqui no WebSite.
Ver matérias relacionadas, para mais informações.
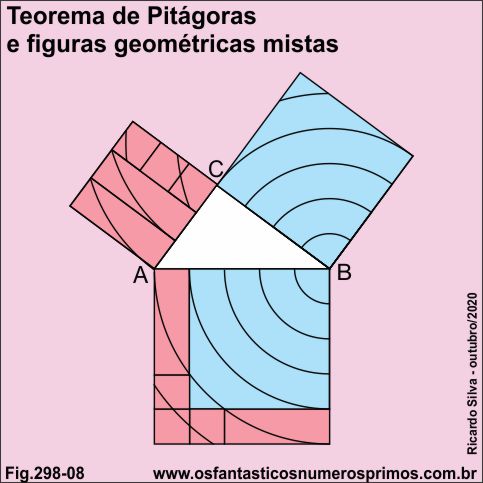
A partir do ponto B, traçou-se arcos de circunferências concêntricos e equidistantes nas áreas dos quadrados do cateto maior e da hipotenusa.
Inclinando o quadrado do cateto maior para a esquerda até a hipotenusa e posteriormente fazendo um giro de 180 graus, o grafismo, isto é, o desenho do cateto maior coincidirá com o desenho sobre o quadrado da hipotenusa.
O quadrado do cateto menor foi dividido em quatro áreas, dois retângulos e três quadradinhos.
No quadrado da hipotenusa, um retângulo foi colocado no canto esquerdo superior, o outro no canto direito inferior e os quadradinhos formando uma letra L "éle" no canto esquerdo inferior.
Observação importante:
O quinto arco de circunferência toca os vértices opostos dos retângulos como se fossem linhas diagonais.
O quinto arco de circunferência toca exatamente as larguras e os comprimentos dos retângulos, deixando "sobrar" os três quadradinhos.
E o mais interessante nesta construção geométrica é que a partir de pontos notáveis como ponto médio, ponto de 1/4 dos lados do quadrado do cateto maior determina-se os arcos de circunferências nos retângulos e quadradinhos do quadrado do cateto menor.
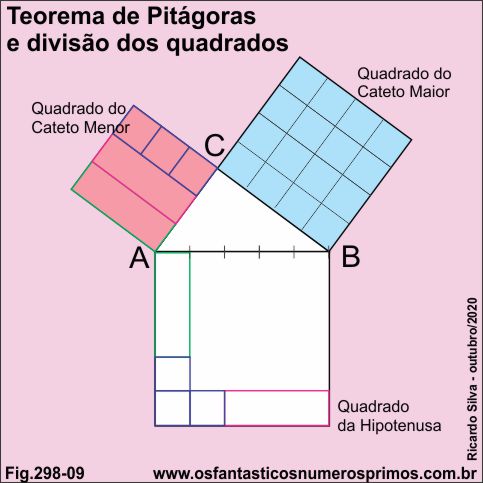
Constrói-se um triângulo retângulo de lados 3-4-5 e os quadrados dos catetos e da hipotenusa em seus respectivos lados.
Dividi-se a hipotenusa em 5 unidades.
Dividi-se a área do cateto maior em 16 quadrados.
Dividi-se a área do cateto menor em 2 retângulos e 3 quadrados.
No quadrado da hipotenusa aloca-se os 2 retângulos e os 3 quadrados referente a área do cateto menor.
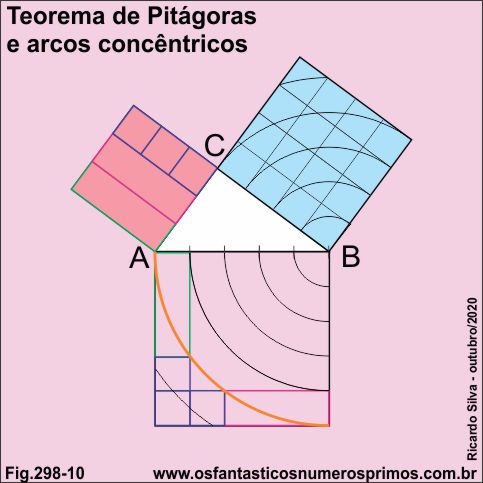
Com centro em B traça-se arcos de circunferências a partir das divisões da hipotenusa no quadrado do cateto maior e no quadrado da hipotenusa.
O quinto arco de circunferência (cor laranja) intersecta os vértices do dois retângulos como se fossem diagonais.
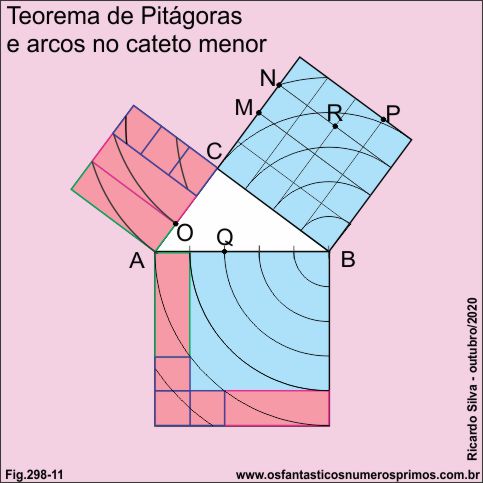
Com centro em M e abertura em A, trace-se o arco no primeiro retângulo.
Com centro em N e abertura em O, traça-se o arco no segundo retângulo.
Com centro em P e abertura em Q, traça-se o arco nos dois pequenos quadrados simultaneamente.
Com centro em R e mesma abertura de PQ, traça-se o arco no terceiro pequeno quadrado.
Autor: Ricardo Silva - outubro/2020
LOOMIS, Elisha Scott. The Pythagorean Propositions - Classics in Mathematics Education Serie - by The National Council of Teachers of Mathematics, Inc. - 1968
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
SPARKS, John C. Pythagorean Theorem – Crowl Jewl of Mathematics, edição digital de 2008.
https://pt.wikipedia.org/
https://en.wikipedia.org/
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato