


Triângulo Retângulo Pitagórico pode ser desenhado de várias formas, entre elas:
a) em folha de papel quadriculado;
b) nos cantos de uma folha de papel, aproveitando o ângulo reto;
c) a partir de duas retas perpendiculares simplesmente marcando seu comprimento e altura e posteriormente a hipotenusa.
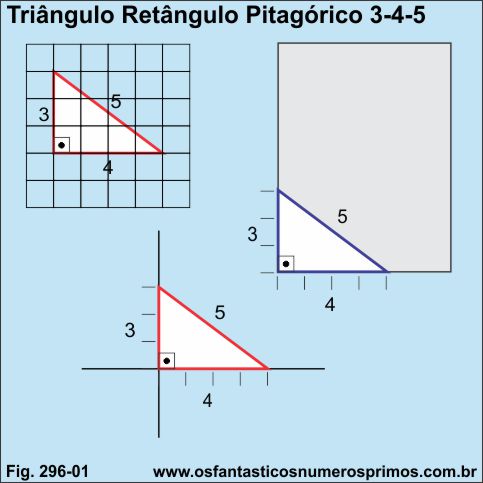
Triângulo Retângulo Pitagórico também pode ser construído com objetos, como barbante ou corda com 12 nós equidistantes.
Estas versatilidadades e facilidades de desenhos e contruções de Triângulos Retângulo Pitagóricos são porque eles são formados por números inteiros, isto é, os seus lados: catetos e hipotenusa tem medidas de Terno Pitagórico.
Terno Pitagórico é um conjunto de três números inteiros que satisfazem o Teorema de Pitágoras a²=b²+c² e que tem o seguinte enunciado:
O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
O primeiro triângulo retângulo cujas medidas dos lados são formados por números inteiros é o Triângulo Retângulo Pitagórico 3-4-5.
O triângulo retângulo 3-4-5 já era de conhecimento de antigas civilizações como: mesopotâmica, egípcia, indiana, chinesa, etc... e foram os estudiosos gregos que o generalizaram para qualquer triângulo retângulo.
Diferentemente do Triângulo Pitagórico, o Triângulo Retângulo de 30-60-90 graus pode ser construído em semicircunferências de quaisquer tamanhos com régua não graduada e compasso, pois seus vértices possuem pontos comuns e notáveis com circunferência e semicircunferência.
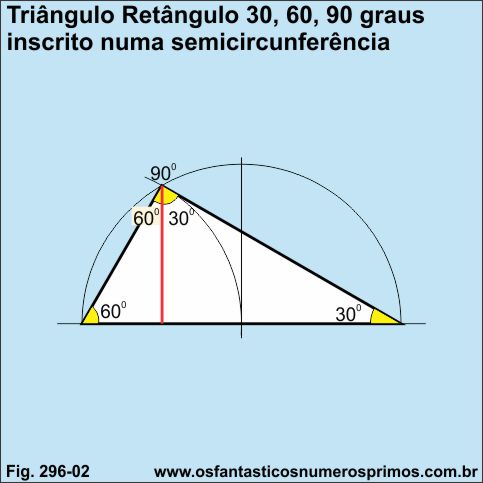
Triângulo Pitágorico construído a partir de uma semicircunferência precisa necessariamente que o diâmetro tenha comprimentro em número inteiro, relacionado a terno pitagórico, o qual pode ser determinado por meio de régua graduada ou por meio do método de divisão de um segmento em partes iguais.
Triângulos Pitagóricos inscritos em semicircunferências apresentam interessantes propriedades e padrões geométricos que serão apresentadas a seguir.
Vésica Piscis é uma construção geométrica com duas circunferências de mesmo raio na qual o centro de uma está sobre a circunferência da outra.
Entre diversas construções de polígonos, com a Vesica Piscis podem ser contruídos triângulos equiláteros e triângulos retângulos de angulos de 30-60-90 graus de diversos tamanhos.
Em duas de suas contruçôes elementarares, o segmento perpendicular que une os dois pontos de intersecções da duas circunferências tem como medida a raiz quadrada de 3 [√3] e contruindo-se um quadrado duplo tem-se a raiz quadrada de 2 [√2] e a raiz quadrada de 5 [√5].
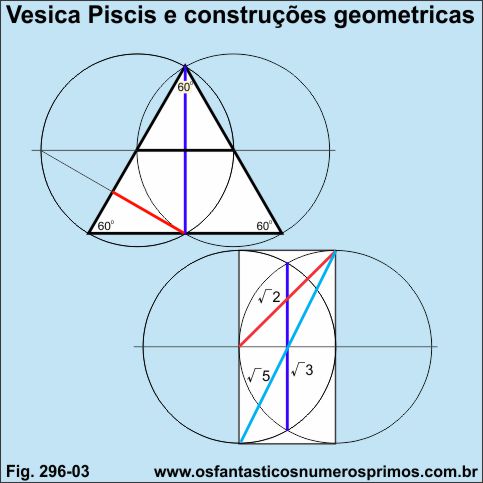
Todo triângulo inscrito numa semicircunferência é triângulo retângulo.
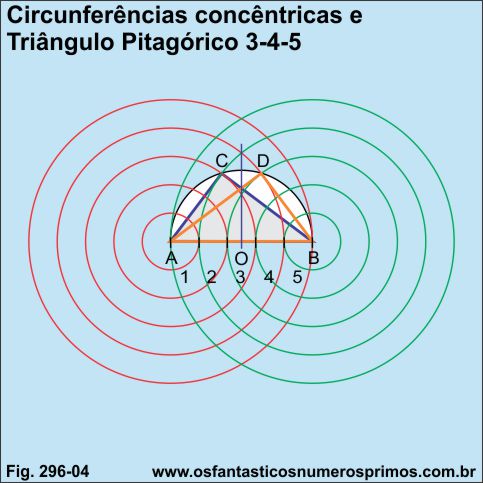
Construindo-se dois conjuntos de circunferências concêntricas a partir de cada extremidade do diâmetro dividido em partes iguais de uma semicircunferência e se duas duplas de circunferências intersectarem a semicircunferência então tem-se triângulos pitagóricos congruentes.
Na Fig.286-04 tem-se o exemplo do diâmetro da semicircunferência dividido em 5 partes.
5 é o termo do terno pitagórico 3-4-5 que corresponde a hipotenusa.
Duas duplas de circunferências concêntricas intersectam a semicircunferência nos pontos C e D.
Unindo-se os pontos A, B e C, obtem-se o primeiro Triângulo Pitagórico 3-4-5.
Unindo-se os pontos A, B e D, obtem-se o segundo Triângulo Pitagórico 3-4-5.
Interessante observar nesta contrução geométrica que ela se assemelha à Vesica Piscis, mas tendo como base a semicircunferência e as circunferências concêntricas.
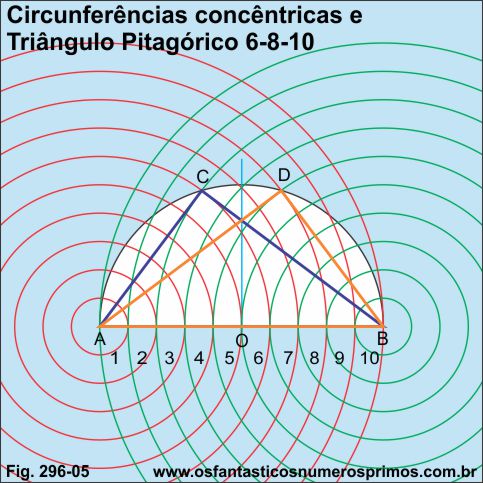
O terno pitagórico 6-8-10 é um terno pitagórico derivado do terno 3-4-5.
Semicircunferência dividida em 10 partes.
10 é o termo do terno pitagórico 6-8-10 que se refere a hipotenusa.
Duas duplas de circunferências concêntricas intersectam a semicircunferência nos pontos C e D.
Unindo-se os pontos A, B e C, obtem-se o primeiro Triângulo Pitagórico 6-8-10.
Unindo-se os pontos A, B e D, obtem-se o segundo Triângulo Pitagórico 6-8-10.
Autor: Ricardo Silva - outubro/2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato