


Em um Artigo publicado na Word Wide Web, cujo título é Complementos sobre o Teorema de Pitágoras, de autoria do Professor Ilydio Sá - Universidade do Estado do Rio de Janeiro – Prática Pedagógica em Matemática 1, é apresentado o seguinte problema:
Os Triângulos Pitagóricos e o perímetro da fazenda
"Uma grande fazenda tem uma forma que pode ser visualizada como um quadrado e quatro triângulos retângulos, de forma que cada um dos triângulos tem um cateto coincidente com um dos lados do quadrado. Veja um modelo dessa fazenda.
Sabemos que todos os triângulos são diferentes em tamanho, mas com a propriedade de terem seus lados expressos por um número inteiro de quilômetros. Qual o MENOR perímetro possível para essa fazenda?
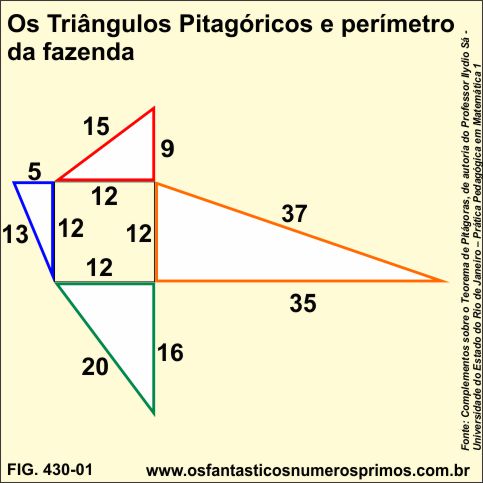
Na questão proposta, percebemos pela figura, que temos de encontrar quatro triângulos retângulos, com os lados expressos por números inteiros (Pitagóricos, portanto), cujos perímetros sejam os menores possíveis e que tenham um lado comum (com a mesma medida). É uma simples questão de investigação. Olhando-se na tabela abaixo (o grifo é nosso), vemos que os triângulos (de menores perímetros) que atendem às condições do problema são: (9, 12, 15) - (5, 12, 13) - (12, 16, 20) - (12, 35, 37)"
Resposta: O perímetro da fazenda será igual a: 5 + 15 + 9 + 37 + 35 + 16 + 20 + 13 = 150 km.
Questão extraída de: “A Magia da Matemática – Ilydio Pereira de Sá Ed. Ciência Moderna, 2007.
Dados dois números naturais m>n, o terno (a,b,c), onde:
a = m² - n²
b = 2mn
c = m² + n²
é pitagórico, e é primitivo se e somente se m e n são primos entre si e possuem paridades distintas.
Observação importante: As Fórmulas de Euclides não geram todos os ternos pitagóricos derivados.
O leitor / visitante atento notará na tabela abaixo que o Terno Pitagórico Derivado (9, 12, 15) não está presente, pois ele não pode ser gerado pelas Fórmulas de Euclides.
Ternos pitagóricos cujas ordens / posições são números triangulares: 1, 3, 6, 10, 15, ... são ternos primitivos e com os quais podem ser gerados infinitos ternos pitagóricos derivados.
Aqui no WebSite Os Fantásticos Números Primos, bem como no livro digital Ternos Pitagóricos e Sequências Numéricas, os ternos pitagóricos cujas ordens / posições são números triangulares são denominados de Ternos Pitagóricos Primitivos de Ordem Triangular.
A tabela a seguir apresenta os primeiros 21 ternos pitagóricos primitivos e derivados, inclusive 3 ternos do problema acima (células azuis, verdes, laranjas) gerados pelas Fórmulas de Euclides.
| Ternos Pitagóricos | |||
| gerados pelas | |||
| Fórmulas de Euclides | |||
| ordem / | Ternos | ||
| posição | a | b | c |
| 1 | 3 | 4 | 5 |
| 2 | 8 | 6 | 10 |
| 3 | 5 | 12 | 13 |
| 4 | 15 | 8 | 17 |
| 5 | 12 | 16 | 20 |
| 6 | 7 | 24 | 25 |
| 7 | 24 | 10 | 26 |
| 8 | 21 | 20 | 29 |
| 9 | 16 | 30 | 34 |
| 10 | 9 | 40 | 41 |
| 11 | 35 | 12 | 37 |
| 12 | 32 | 24 | 40 |
| 13 | 27 | 36 | 45 |
| 14 | 20 | 48 | 52 |
| 15 | 11 | 60 | 61 |
| 16 | 48 | 14 | 50 |
| 17 | 45 | 28 | 53 |
| 18 | 40 | 42 | 58 |
| 19 | 33 | 56 | 65 |
| 20 | 24 | 70 | 74 |
| 21 | 13 | 84 | 85 |
| www.osfantasticosnumerosprimos.com.br | |||
A tabela a seguir apresenta os primeiros ternos pitagóricos derivados do Terno Pitagórico Primitivo 3, 4, 5.
Multiplicando-se cada termo do Terno Pitagórico Primitivo de Ordem Triangular 3, 4, 5 pela sequência de números naturais, obtêm-se infinitos ternos pitagóricos derivados.
O Terno Pitagórico Derivado 9, 12, 15 (células vermelhas) é derivado do Terno Pitagórico Primitivo 3, 4, 5.
| ordem / | Ternos | ||
| posição | a | b | c |
| primitivo | |||
| 1 | 3 | 4 | 5 |
| derivados | |||
| 2 | 6 | 8 | 10 |
| 3 | 9 | 12 | 15 |
| 4 | 12 | 16 | 20 |
| 5 | 15 | 20 | 25 |
| 6 | 18 | 24 | 30 |
| 7 | 21 | 28 | 35 |
| 8 | 24 | 32 | 40 |
| 9 | 27 | 36 | 45 |
| 10 | 30 | 40 | 50 |
Em um outro artigo publicado, em março de 2013, no Blog Manthano, cujo título é:
Um novo olhar sobre os números pitagóricos
"O objetivo desta postagem é publicar um trabalho de autoria do Professor Fernando Cézar Gonçalves Manso (UTFPR-CM) e co-autoria minha (Pedro R.), no qual são apresentados alguns interessantes resultados (com elementares demonstrações) sobre ternos pitagóricos. Tais resultados incluem tanto um algoritmo para gerar todos eles a partir de um cateto dado (vide teorema 1) quanto algumas condições para obter ternos primitivos (vide teorema 2). O BLOG MANTHANO agradece imensamente a contribuição do professor Fernando Manso que, a partir de suas finas observações, tornou possível a elaboração deste conteúdo."
Teorema 1: Seja a um número natural maior do que 2. A fim de que o terno (a, b c) seja pitagórico é necessário, e suficiente, que exista um número natural d < a da mesma paridade de a tal que a2 / d também tenha a mesma paridade de a e tal que se tenha
| a2 - d2 | a2 + d2 | ||||||
| (a, b, c) | = | ( | a, | ____ | , | ___ | ) |
| 2d | 2d |
O Blog traz também um outro interessante problema relacionado ao número 12.
"Exercício 2: encontrar o triângulo retângulo de menor perímetro e lados inteiros, cujo um dos catetos mede 12.
Solução: pelo teorema 1, o perímetro de qualquer triângulo retângulo de lados inteiros pode se escrito sob a forma:
| a2 - d2 | a2 + d2 | a2 | ||||||||
| P | = | a | + | ____ | + | ___ | = | a | + | __ |
| 2d | 2d | d |
Fixando a , vemos que P assumirá o menor valor quando d assumir o maior possível. Como d = 8 é o maior divisor par de 122 = 144 menor do que 12 e que proporciona um quociente par, o triângulo procurado é aquele no qual a = 12, b = 5 e c = 13."
12 + 5 + 13 = 30
De fato, utilizando-se a Fórmula do Teorema 1, consegue-se gerar a partir do número 12, os ternos pitagóricos que também podem ser gerados pelas Fórmulas de Euclides:
(12, 35, 37),
(12, 16, 20)
e (12, 5, 13)
e o que também não pôde ser gerado pelas Fórmulas de Euclides:
(12, 9, 15).
No mesmo artigo é publicado Exemplo 2 de como gerar ternos pitagóricos a partir do número 102.
"Exemplo 2: o teorema 1 nos dá uma maneira de determinar todos os ternos a partir de um dado cateto. Por exemplo, se quisermos determinar todos os ternos tais que um dos catetos seja 102 podemos proceder da seguinte maneira:
- Encontramos todos os divisores de 1022 = 10.404 menores do que 102 : 1, 2, 3, 4, 6, 9, 12, 17, 18, 34, 36, 51, 68.
- Selecionamos os que possuem a mesma paridade de 102: 2, 4, 6, 12, 18, 34, 36, 68.
- Filtramos os que, ao dividirem 1022, forneçam um quociente da mesma paridade de: 2, 6, 18, 34.
- Fazemos a = 102 e d = 2, 6, 18 e 34 na fórmula dada pelo teorema. Os ternos procurados são, portanto,
(102, 2600, 2602),
(102, 136, 870),
(102, 280, 298),
e (102, 136, 170)."
Um outro método de se obter (parte) determinados ternos pitagóricos é através de divisores ímpares de um número.
Sabendo-se que o primeiro termo de um terno pitagórico primitivo é um número ímpar, formamos então um terno pitagórico primitivo e posteriormente ternos pitagóricos derivados.
Exemplo:
Número 90
Divisores de 90
12 divisores
D (90): {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90}
Divisores ímpares maiores que 1 de 90: 3, 5, 9, 15 e 45
A tabela a seguir apresenta os divisores de 90 formando pares multiplicativos, isto é, o primeiro divisor com o último divisor; o segundo divisor com o penúltimo divisor e assim sucessivamente.
| Divisores de 90 | ||
| (pares multiplicativos) | ||
| fatores | fatores | produto |
| 1 | 90 | 90 |
| 2 | 45 | 90 |
| 3 | 30 | 90 |
| 5 | 18 | 90 |
| 6 | 15 | 90 |
| 9 | 10 | 90 |
| www.osfantasticosnumerosprimos.com.br | ||
O divisor 3 faz parte do Terno Pitagórico Primitivo 3, 4, 5.
3 é o primeiro termo do Terno Pitagórico Primitivo 3, 4, 5.
90 : 3 = 30
30 é ordem / posição do Terno Pitagórico Derivado 90, 120, 150 do Terno Pitagórico Primitivo 3, 4, 5 pois:
30 x 3 = 90
30 x 4 = 120
30 x 5 = 150
O divisor 5 faz parte do Terno Pitagórico Primitivo 5, 12, 13.
5 é o primeiro termo do Terno Pitagórico Primitivo 5, 12, 13.
90 : 5 = 18
18 é ordem / posição do Terno Pitagórico Derivado 90, 216, 234 do Terno Pitagórico Primitivo 5, 12, 13 pois:
18 x 5 = 90
18 x 12 = 216
18 x 13 = 234
O divisor 9 faz parte do Terno Pitagórico Primitivo 9, 40, 41.
9 é o primeiro termo do Terno Pitagórico Primitivo 9, 40, 41.
90 : 9 = 10
10 é ordem / posição do Terno Pitagórico Derivado 90, 400, 410 do Terno Pitagórico Primitivo 9, 40, 41 pois:
10 x 9 = 90
10 x 40 = 400
10 x 41 = 410
O divisor 15 faz parte do Terno Pitagórico Primitivo 15, 112, 113.
15 é o primeiro termo do Terno Pitagórico Primitivo 15, 112, 113.
90 : 15 = 6
6 é ordem / posição do Terno Pitagórico Derivado 90, 672, 678 do Terno Pitagórico Primitivo 5, 112, 113 pois:
6 x 15 = 90
6 x 112 = 672
6 x 113 = 678
O divisor 45 faz parte do Terno Pitagórico Primitivo 45, 1012, 1013.
45 é o primeiro termo do Terno Pitagórico Primitivo 15, 1012, 1013.
90 : 45 = 2
2 é ordem / posição do Terno Pitagórico Derivado 90, 2024, 2026 do Terno Pitagórico Primitivo 15, 1012, 1013 pois:
2 x 45 = 90
2 x 1012 = 2024
2 x 1013 = 2026
primeiro: 90 - 120 - 150
segundo: 90 - 216 - 234
terceiro: 90 - 400 - 410
quarto: 90 - 672 - 678
quinto: 90 - 2024 - 2026
A título de curiosidade, os números menores que 500:
a) 90, 150, 198, 234, 294, 306, 342, 350, 486 e 414 que possuem 12 divisores, entre eles, 6 divisores ímpares e 6 divisores pares;
b) 315 e 495 que possuem 12 divisores ímpares.
Autor: Ricardo Silva - maio/2023
PEREIRA, Ilydio de Sá. A Magia da Matemática – Ed. Ciência Moderna, 2007.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
manthanos.blogspot.com

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato