


Ternos Pitagóricos são sequências de 3 números inteiros que têm relação como o Teorema de Pitágoras que diz que: "A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa" ou "O quadrado da hipotenusa é igual a soma dos quadrados dos catetos", representado pela fórmula:
a² = b² + c²
Neste estudo são apresentados interessantes relações numéricas entre grupos de ternos pitagóricos, isto é, grupos de sequências de ternos pitagóricos derivados a partir de um terno pitagórico primitivo.
Terno pitagórico primitivo é uma sequência de 3 números inteiros com o qual podem ser derivados infinitos outros ternos pitagóricos, multiplicando-os pela sequência de números naturais.
Euclides, em seu livro Elementos, demonstrou que existe uma infinidade de ternos pitagóricos primitivos. Além disso, encontrou fórmulas que geram todos os ternos pitagóricos primitivos. Dados dois números naturais m>n, o terno (a,b,c), onde:
a = m² - n²
b = 2mn
c = m² + n²
é pitagórico, e é primitivo se e somente se m e n são primos entre si e possuem paridades distintas.
Fonte: https://pt.wikipedia.org/
As Fórmulas de Euclides, conforme tabela abaixo, também geram determinados ternos pitagóricos derivados a partir de números não primos entre si.
Observação importante 1: conforme estudos publicados no livro digital Ternos Pitagóricos e Sequências Numéricas e aqui no WebSite Os Fantásticos Números Primos, as Fórmulas de Euclides não geram todos os ternos pitagóricos derivados sequêncialmente.
Observação importante 2: conforme estudos publicados no livro digital Ternos Pitagóricos e Sequências Numéricas e aqui no WebSite Os Fantásticos Números Primos, os ternos pitagóricos primitivos gerados pelas Fórmulas de Euclides têm ordens / posições de números triangulares.
A presente tabela demonstra os 36 primeiros ternos pitagóricos primitivos e derivados.
Os ternos pitagóricos cujas ordens / posições são números triangulares (células verdes) são ternos pitagóricos primitivos e neste estudo são denominados de Ternos Pitagóricos Primitivos de Ordem Triangular.
Ternos Pitagóricos Primitivos de Ordem Triangular apresentam as seguintes características:
a) o primeiro e terceiro termos são números ímpares;
b) o segundo e terceiro termos são números consecutivos;
c) a soma do segundo e terceiro termos tem como resultado um número quadrado perfeito;
d) o segundo termo é um número múltiplo de número 4;
Exemplos:
3, 4, 5
5, 12, 13
7, 24, 25
9, 40, 41
e) O primeiro termo de um Terno Pitagórico Primitivo de Ordem Triangular faz parte da sequência de números ímpares a partir de 3: 3, 5, 7, 9, 11, 13, 15, 17, ...
Os Ternos Pitagóricos Primitivos de Ordem Triangular são formados em ordem crescente enquanto outros não, como:
8, 6, 10
15, 8, 17
24, 10, 26
Os ternos pitagóricos derivados são o dobro, do dobro, do dobro,... de ternos pitagóricos primitivos:
Exemplos:
3, 4, 5 (terno primitivo)
6, 8, 10 (terno derivado - dobro de 3, 4, 5)
12, 16, 20 (terno derivado - dobro de 6, 8, 10)
24, 32, 40 (terno derivado - dobro de 12, 16, 20)
e assim sucessivamente...
| Ternos Pitagóricos | |||
| Primitivos e Derivados | |||
| Ordem / | |||
| Posição | |||
| 1 | 3 | 4 | 5 |
| 2 | 8 | 6 | 10 |
| 3 | 5 | 12 | 13 |
| 4 | 15 | 8 | 17 |
| 5 | 12 | 16 | 20 |
| 6 | 7 | 24 | 25 |
| 7 | 24 | 10 | 26 |
| 8 | 21 | 20 | 29 |
| 9 | 16 | 30 | 34 |
| 10 | 9 | 40 | 41 |
| 11 | 35 | 12 | 37 |
| 12 | 32 | 24 | 40 |
| 13 | 27 | 36 | 45 |
| 14 | 20 | 48 | 52 |
| 15 | 11 | 60 | 61 |
| 16 | 48 | 14 | 50 |
| 17 | 45 | 28 | 53 |
| 18 | 40 | 42 | 58 |
| 19 | 33 | 56 | 65 |
| 20 | 24 | 70 | 74 |
| 21 | 13 | 84 | 85 |
| 22 | 63 | 16 | 65 |
| 23 | 60 | 32 | 68 |
| 24 | 55 | 48 | 73 |
| 25 | 48 | 64 | 80 |
| 26 | 39 | 80 | 89 |
| 27 | 28 | 96 | 100 |
| 28 | 15 | 112 | 113 |
| 29 | 80 | 18 | 82 |
| 30 | 77 | 36 | 85 |
| 31 | 72 | 54 | 90 |
| 32 | 65 | 72 | 97 |
| 33 | 56 | 90 | 106 |
| 34 | 45 | 108 | 117 |
| 35 | 32 | 126 | 130 |
| 36 | 17 | 144 | 145 |
| www.osfantasticosnumerosprimos.com.br | |||
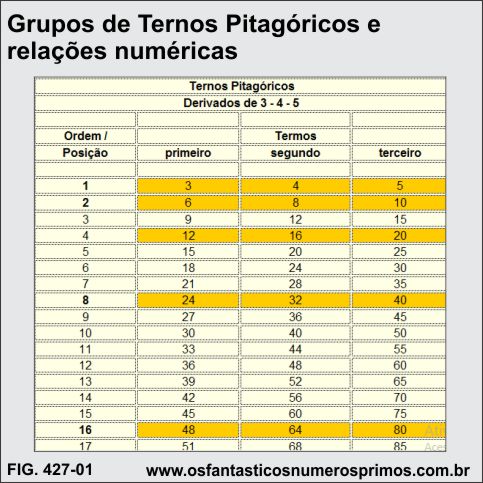
A presente tabela demonstra os 20 primeiros ternos pitagóricos derivados do Terno Primitivo 3, 4, 5.
Multiplicando-se o Terno Pitagórico Primitivo 3, 4, 5 pela sequência de números naturais, obtêm-se infinitos ternos pitagóricos derivados.
Os ternos pitagóricos cujas ordens / posições são potências de base 2: 1, 2, 4, 8, 16, ... (células laranjas) são ternos que também podem ser gerados pelas Fórmulas de Euclides.
Os demais ternos derivados não são gerados pelas Fórmulas de Euclides.
Exemplos:
9, 12, 15
15, 20, 25
18, 24, 30 e outros.
| Ternos Pitagóricos | |||
| Derivados de 3 - 4 - 5 | |||
| Ordem / | Termos | ||
| Posição | primeiro | segundo | terceiro |
| 1 | 3 | 4 | 5 |
| 2 | 6 | 8 | 10 |
| 3 | 9 | 12 | 15 |
| 4 | 12 | 16 | 20 |
| 5 | 15 | 20 | 25 |
| 6 | 18 | 24 | 30 |
| 7 | 21 | 28 | 35 |
| 8 | 24 | 32 | 40 |
| 9 | 27 | 36 | 45 |
| 10 | 30 | 40 | 50 |
| 11 | 33 | 44 | 55 |
| 12 | 36 | 48 | 60 |
| 13 | 39 | 52 | 65 |
| 14 | 42 | 56 | 70 |
| 15 | 45 | 60 | 75 |
| 16 | 48 | 64 | 80 |
| 17 | 51 | 68 | 85 |
| 18 | 54 | 72 | 90 |
| 19 | 57 | 76 | 95 |
| 20 | 60 | 80 | 100 |
| www.osfantasticosnumerosprimos.com.br | |||
A presente tabela demonstra os 20 primeiros ternos pitagóricos derivados do Terno Primitivo 5, 12, 13.
Multiplicando-se o Terno Pitagórico Primitivo 5, 12, 13 pela sequência de números naturais, obtêm-se infinitos ternos pitagóricos derivados.
Os ternos pitagóricos cujas ordens / posições são potências de base 2: 1, 2, 4, 8, 16, ... (células laranjas) são ternos que também podem ser gerados pelas Fórmulas de Euclides.
Os demais ternos derivados não são gerados pelas Fórmulas de Euclides.
Exemplos:
15, 36, 39
25, 60, 65
30, 72, 78 e outros.
| Ternos Pitagóricos | |||
| Derivados de 5 - 12 - 13 | |||
| Ordem / | Termos | ||
| Posição | primeiro | segundo | terceiro |
| 1 | 5 | 12 | 13 |
| 2 | 10 | 24 | 26 |
| 3 | 15 | 36 | 39 |
| 4 | 20 | 48 | 52 |
| 5 | 25 | 60 | 65 |
| 6 | 30 | 72 | 78 |
| 7 | 35 | 84 | 91 |
| 8 | 40 | 96 | 104 |
| 9 | 45 | 108 | 117 |
| 10 | 50 | 120 | 130 |
| 11 | 55 | 132 | 143 |
| 12 | 60 | 144 | 156 |
| 13 | 65 | 156 | 169 |
| 14 | 70 | 168 | 182 |
| 15 | 75 | 180 | 195 |
| 16 | 80 | 192 | 208 |
| 17 | 85 | 204 | 221 |
| 18 | 90 | 216 | 234 |
| 19 | 95 | 228 | 247 |
| 20 | 100 | 240 | 260 |
| www.osfantasticosnumerosprimos.com.br | |||
A presente tabela demonstra os 20 primeiros ternos pitagóricos derivados do Terno Primitivo 7, 24, 25.
Multiplicando-se o Terno Pitagórico Primitivo 7, 24, 25 pela sequência de números naturais, obtêm-se infinitos ternos pitagóricos derivados.
Os ternos pitagóricos cujas ordens / posições são potências de base 2: 1, 2, 4, 8, 16, ... (células laranjas) são ternos que também podem ser gerados pelas Fórmulas de Euclides.
Os demais ternos derivados não são gerados pelas Fórmulas de Euclides.
Exemplos:
21, 72, 75
35, 120, 125
42, 144, 150 e outros.
| Ternos Pitagóricos | |||
| Derivados de 7 - 24 - 25 | |||
| Ordem / | Termos | ||
| Posição | primeiro | segundo | terceiro |
| 1 | 7 | 24 | 25 |
| 2 | 14 | 48 | 50 |
| 3 | 21 | 72 | 75 |
| 4 | 28 | 96 | 100 |
| 5 | 35 | 120 | 125 |
| 6 | 42 | 144 | 150 |
| 7 | 49 | 168 | 175 |
| 8 | 56 | 192 | 200 |
| 9 | 63 | 216 | 225 |
| 10 | 70 | 240 | 250 |
| 11 | 77 | 264 | 275 |
| 12 | 84 | 288 | 300 |
| 13 | 91 | 312 | 325 |
| 14 | 98 | 336 | 350 |
| 15 | 105 | 360 | 375 |
| 16 | 112 | 384 | 400 |
| 17 | 119 | 408 | 425 |
| 18 | 126 | 432 | 450 |
| 19 | 133 | 456 | 475 |
| 20 | 140 | 480 | 500 |
| www.osfantasticosnumerosprimos.com.br | |||
Grupos de ternos pitagóricos são sequências de ternos derivados gerados a partir de um terno pitagórico primitivo
A diferença entre os segundos e primeiros termos correspondentes do Terno Pitagórico Primitivo 3, 4, 5 e seus derivados formam a sequência de números naturais.
A diferença entre os terceiros e segundos termos correspondentes do Terno Pitagórico Primitivo 3, 4, 5 e seus derivados formam a sequência de números naturais.
A soma do primeiro termo (3) com o segundo termo (4) do Terno Pitagórico Primitivo 3, 4, 5 é 7.
7 é a diferença entre o segundo termo (12) e o primeiro termo (5) do Terno Pitagórico Primitivo 5, 12, 13.
| Terno Pitagórico Primitivo 3, 4, 5 | ||||
| e derivados | ||||
| Diferença | Diferença | |||
| Números | Números | |||
| Naturais | Naturais | |||
| 3 | (1) | 4 | (1) | 5 |
| 6 | (2) | 8 | (2) | 10 |
| 9 | (3) | 12 | (3) | 15 |
| 12 | (4) | 16 | (4) | 20 |
| 15 | (5) | 20 | (5) | 25 |
| 18 | (6) | 24 | (6) | 30 |
| 21 | (7) | 28 | (7) | 35 |
| 24 | (8) | 32 | (8) | 40 |
| 27 | (9) | 36 | (9) | 45 |
| 30 | (10) | 40 | (10) | 50 |
| www.osfantasticosnumerosprimos.com.br | ||||
A soma dos primeiros e segundos termos do Terno Pitagórico Primitivo 3, 4, 5 e seus derivados correspondem as diferenças entre os segundos e primeiros termos do Terno Pitagórico Primitivo 5, 12, 13 e seus derivados.
A diferença entre segundos e primeiros termos correspondentes do Terno Pitagórico 5, 12, 13 e seus derivados formam múltiplos de 7.
A diferença entre terceiros e segundos termos correspondentes do Terno Pitagórico 5, 12, 13 e seus derivados formam a sequência de números naturais.
A soma do primeiro termo (3) com o segundo termo (4) do Terno Pitagórico Primitivo 3, 4, 5 é 7.
7 é a diferença entre o segundo termo (12) e o primeiro termo (5) do Terno Pitagórico Primitivo 5, 12, 13.
| Terno Pitagórico Primitivo 5, 12, 13 | ||||
| e derivados | ||||
| Diferença | Diferença | |||
| Múltiplos de 7 | Números | |||
| Naturais | ||||
| 5 | (7) | 12 | (1) | 13 |
| 10 | (14) | 24 | (2) | 26 |
| 15 | (21) | 36 | (3) | 39 |
| 20 | (28) | 48 | (4) | 52 |
| 25 | (35) | 60 | (5) | 65 |
| 30 | (42) | 72 | (6) | 78 |
| 35 | (49) | 84 | (7) | 91 |
| 40 | (56) | 96 | (8) | 104 |
| 45 | (63) | 108 | (9) | 117 |
| 50 | (70) | 120 | (10) | 130 |
| www.osfantasticosnumerosprimos.com.br | ||||
A soma dos primeiros e segundos termos do Terno Pitagórico Primitivo 5, 12, 13 e seus derivados correspondem as diferenças entre os segundos e primeiros termos do Terno Pitagórico Primitivo 7, 24, 25 e seus derivados.
A diferença entre segundos e primeiros termos correspondentes do Terno Pitagórico 7, 24, 25 e seus derivados formam múltiplos de 17.
A diferença entre terceiros e segundos termos correspondentes do Terno Pitagórico 7, 24, 25 e seus derivados formam a sequência de números naturais.
A soma do primeiro termo (5) com o segundo termo (12) do Terno Pitagórico Primitivo 5, 12, 13 é 17.
17 é a diferença entre o segundo termo (24) e o primeiro termo (7) do Terno Pitagórico Primitivo 7, 24, 25.
| Terno Pitagórico Primitivo 7, 24, 25 | ||||
| e derivados | ||||
| Diferença | Diferença | |||
| Múltiplos de 17 | Números | |||
| Naturais | ||||
| 7 | (17) | 24 | (1) | 25 |
| 14 | (34) | 48 | (2) | 50 |
| 21 | (51) | 72 | (3) | 75 |
| 28 | (68) | 96 | (4) | 100 |
| 35 | (85) | 120 | (5) | 125 |
| 42 | (102) | 144 | (6) | 150 |
| 49 | (119) | 168 | (7) | 175 |
| 56 | (136) | 192 | (8) | 200 |
| 63 | (153) | 216 | (9) | 225 |
| 70 | (170) | 240 | (10) | 250 |
| www.osfantasticosnumerosprimos.com.br | ||||
A soma dos primeiros e segundos termos do Terno Pitagórico Primitivo 7, 24, 25 e seus derivados correspondem as diferenças entre os segundos e primeiros termos do Terno Pitagórico Primitivo 9, 40, 41 e seus derivados.
Autor: Ricardo Silva - abril/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato