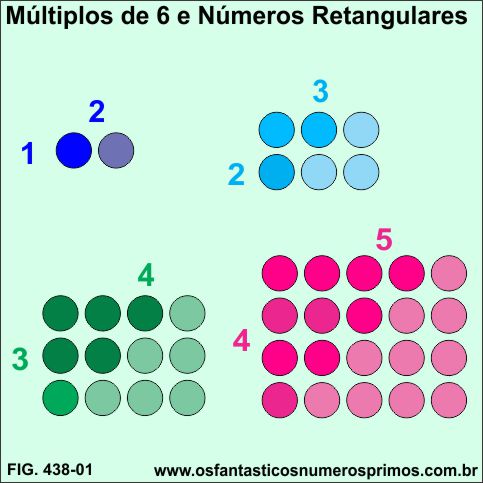
Números retangulares / oblongos, também denominados de números figurados, números geométricos, números poligonais são números que podem ser formados por meio de arranjos de pontos formando figuras geométricas de retângulos.
Os números retangulares estão estritamente relacionados como números triangulares e vice-versa, pois a divisão de um número retangular por 2 gera número triangular ou duplicando-se um número triangular gera-se um número retangular.
O presente estudo demonstra que a partir de múltiplos de 6 também são possíveis de se gerarem determinados números retangulares e consequentemente números triangulares que não são múltiplos de 3.
Podemos obter números retangulares por métodos tradicionais, tais como:
a) do produto de 2 números consecutivos.
Exemplos:
1 x 2 = 2
2 x 3 = 6
3 x 4 = 12
Número retangular dividido por 2 tem como quociente um número triangular.
Exemplos:
2 : 2= 1
6 : 2 = 3
12 : 2 = 6
b) de número quadrado perfeito somado com sua raiz;
Exemplos:
1 + 1 = 2
4 + 2 = 6
9 + 3 = 12
c) de raiz quadrada subtraída de seu quadrado perfeito, a partir do quadrado 4;
Exemplos:
4 - 2 = 2
9 - 3 = 6
16 - 4 = 12
A tabela a seguir apresenta as 37 primeiras somas de números ímpares em suas respectivas ordens / posições, entre elas, duplas de números ímpares cujas somas são números retangulares e suas regularidades numéricas:
a) na coluna ordem / posição, a diferença entre uma posição posterior e anterior é um múltiplo de 6 (células laranjas);
7 - 1 = 6, o mesmo que 6 x 1
19 - 7 = 12, o mesmo que 6 x 2
37 - 19 = 18, o mesmo que 6 x 3
61 - 37 = 24, o mesmo que 6 x 4
Interessante observar que na coluna ordem / posição há ocorrências de números primos.
b) na coluna ímpar, a diferença entre um número ímpar posterior e anterior é um múltiplo de 12 (células laranjas);
13 - 1 = 12, o mesmo que 12 x 1
37 - 13 = 24 , o mesmo que 12 x 2
73 - 37 = 36, o mesmo que 12 x 3
121 - 73 = 48, o mesmo que 12 x 4
Interessante observar que na coluna números ímpares há ocorrências de números primos.
c) na coluna soma, a diferença entre uma soma posterior e anterior é um múltiplo de 18 (células laranjas);
20 - 2 = 18, o mesmo que 18 x 1
56 - 20 = 36, o mesmo que 18 x 2
110 - 56 = 54, o mesmo que 18 x 3
d) na coluna fatores, tem-se os números consecutivos que multiplicados, o resultado é o número retangular da coluna soma (células laranjas);
1 x 2 = 2
2 é um número retangular / oblongo.
1 e 2 são números consecutivos.
4 x 5 = 20
20 é um número retangular / oblongo.
4 e 5 são números consecutivos.
7 x 8 = 56
56 é um número retangular / oblongo.
7 e 8 são números consecutivos.
10 x 11 = 110
110 é um número retangular / oblongo.
10 e 11 são números consecutivos.
Interessante notar que os primeiros fatores: 1, 4, 7, 10, ... formam uma progressão aritmética de razão 3 e os segundos fatores: 2, 5, 8, 11,... também formam uma progressão aritmética de razão 3.
e) na coluna número triangular, a diferença entre um triangular posterior com um anterior é um múltiplo de 9;
10 - 1 = 9, o mesmo que 9x1
28 - 10 = 18, o mesmo que 9x2
55 - 28 = 27, o mesmo que 9x3
f) os número retangulares 2, 20, 56, 110,... não são múltiplos de 3;
g) os números triangulares 1, 10, 28, 55,... não são múltiplos de 3.
| Número Retangular | ||||||
| a partir | ||||||
| da soma de ímpar com sua ordem / posição | ||||||
| número | número | |||||
| retangular | triangular | |||||
| ordem / | número | soma | fatores | soma | ||
| posição | ímpar | dividido | ||||
| por 2 | ||||||
| 1 | + | 1 | = | 2 | 1x2 | 1 |
| 2 | + | 3 | = | 5 | ||
| 3 | + | 5 | = | 8 | ||
| 4 | + | 7 | = | 11 | ||
| 5 | + | 9 | = | 14 | ||
| 6 | + | 11 | = | 17 | ||
| 7 | + | 13 | = | 20 | 4x5 | 10 |
| 8 | + | 15 | = | 23 | ||
| 9 | + | 17 | = | 26 | ||
| 10 | + | 19 | = | 29 | ||
| 11 | + | 21 | = | 32 | ||
| 12 | + | 23 | = | 35 | ||
| 13 | + | 25 | = | 38 | ||
| 14 | + | 27 | = | 41 | ||
| 15 | + | 29 | = | 44 | ||
| 16 | + | 31 | = | 47 | ||
| 17 | + | 33 | = | 50 | ||
| 18 | + | 35 | = | 53 | ||
| 19 | + | 37 | = | 56 | 7x8 | 28 |
| 20 | + | 39 | = | 59 | ||
| 21 | + | 41 | = | 62 | ||
| 22 | + | 43 | = | 65 | ||
| 23 | + | 45 | = | 68 | ||
| 24 | + | 47 | = | 71 | ||
| 25 | + | 49 | = | 74 | ||
| 26 | + | 51 | = | 77 | ||
| 27 | + | 53 | = | 80 | ||
| 28 | + | 55 | = | 83 | ||
| 29 | + | 57 | = | 86 | ||
| 30 | + | 59 | = | 89 | ||
| 31 | + | 61 | = | 92 | ||
| 32 | + | 63 | = | 95 | ||
| 33 | + | 65 | = | 98 | ||
| 34 | + | 67 | = | 101 | ||
| 35 | + | 69 | = | 104 | ||
| 36 | + | 71 | = | 107 | ||
| 37 | + | 73 | = | 110 | 10x11 | 55 |
| www.osfantasticosnumerosprimos.com.br | ||||||
O número 6 é um número perfeito.
O número 6 é o primeiro número que é produto de dois números primos distintos: 2 x 3 = 6.
As potências de base 6 possuem divisores em quantidades de números quadrados perfeitos.
Múltiplos de 6 também apresentam regularidades numéricas com determinadas duplas de números ímpares que somadas, o resultado é um número retangular, vejamos:
Exemplo 1)
a) o 6 (6 x 1) está próximo da parcela 7;
b) 7 é 1 unidade maior que 6;
c) 13 é 1 unidade maior que 12 (6 x 2);
d) 6 + 7 = 13
Por meio da expressão numérica:
{ { 6 x [ ( 1 x 2 ) / 2 ] } + 1} + { {6 [ 2 ( ( 1 x 2 ) / 2 ) ] } + 1 } = 20
ou da expressão algébrica:
{ {6 { [ n (n + 1)] / 2 } + 1 } + { {6 { 2 { [ n (n + 1)] / 2 } } + 1 }
obtem-se determinados números retangulares.
| 6 | + | 11 | = | 17 | ||
| 7 | + | 13 | = | 20 | 4x5 | 10 |
Exemplo 2)
a) o 18 ( 6 x 3) está próximo da parcela 19;
b) 19 é 1 unidade maior que 18;
c) 37 é 1 unidade maior que 36 (6 x 6);
d) 18 + 19 = 37
Por meio da expressão numérica:
{ { 6 x [ ( 2 x 3 ) / 2 ] } + 1} + { {6 [ 2 ( ( 2 x 3 ) / 2 ) ] } + 1 } = 56
ou da expressão algébrica:
{ {6 { [ n (n + 1)] / 2 } + 1 } + { {6 { 2 { [ n (n + 1)] / 2 } } + 1 }
obtem-se determinados números retangulares.
| 18 | + | = | ||||
| 19 | + | 37 | = | 56 | 7x8 | 28 |
Interessante observar que 28 é um número perfeito.
Exemplo 3)
a) o 36 (6 x 6) está próximo da parcela 37;
b) 37 é 1 unidade maior que 36;
c) 73 é 1 unidade maior que 72 (6 x 12);
d) 36 + 37 = 73
Por meio da expressão numérica:
{ { 6 x [ ( 3 x 4 ) / 2 ] } + 1} + { {6 [ 2 ( ( 3 x 4 ) / 2 ) ] } + 1 } = 110
ou da expressão algébrica:
{ {6 { [ n (n + 1)] / 2 } + 1 } + { {6 { 2 { [ n (n + 1)] / 2 } } + 1 }
obtem-se determinados números retangulares.
| 36 | + | = | ||||
| 37 | + | 73 | = | 110 | 10x11 | 55 |
A tabela a seguir apresenta os 50 primeiros números retangulares gerados a partir da soma de produtos de 6 por triangulares somados com 1 unidade mais o produto de 6 por dobros de triangulares correspondentes somados com 1 unidade.
| Múltiplos de 6 | ||||||||||
| e números retangulares | ||||||||||
| soma | ||||||||||
| dos | ||||||||||
| número | produto | dobro | produto | produtos | ||||||
| triangular | triangular | (retangular) | ||||||||
| 6 | x | 1 | = | 7 | 6 | x | 2 | = | 13 | 20 |
| 6 | x | 3 | = | 19 | 6 | x | 6 | = | 37 | 56 |
| 6 | x | 6 | = | 37 | 6 | x | 12 | = | 73 | 110 |
| 6 | x | 10 | = | 61 | 6 | x | 20 | = | 121 | 182 |
| 6 | x | 15 | = | 91 | 6 | x | 30 | = | 181 | 272 |
| 6 | x | 21 | = | 127 | 6 | x | 42 | = | 253 | 380 |
| 6 | x | 28 | = | 169 | 6 | x | 56 | = | 337 | 506 |
| 6 | x | 36 | = | 217 | 6 | x | 72 | = | 433 | 650 |
| 6 | x | 45 | = | 271 | 6 | x | 90 | = | 541 | 812 |
| 6 | x | 55 | = | 331 | 6 | x | 110 | = | 661 | 992 |
| 6 | x | 66 | = | 397 | 6 | x | 132 | = | 793 | 1190 |
| 6 | x | 78 | = | 469 | 6 | x | 156 | = | 937 | 1406 |
| 6 | x | 91 | = | 547 | 6 | x | 182 | = | 1093 | 1640 |
| 6 | x | 105 | = | 631 | 6 | x | 210 | = | 1261 | 1892 |
| 6 | x | 120 | = | 721 | 6 | x | 240 | = | 1441 | 2162 |
| 6 | x | 136 | = | 817 | 6 | x | 272 | = | 1633 | 2450 |
| 6 | x | 153 | = | 919 | 6 | x | 306 | = | 1837 | 2756 |
| 6 | x | 171 | = | 1027 | 6 | x | 342 | = | 2053 | 3080 |
| 6 | x | 190 | = | 1141 | 6 | x | 380 | = | 2281 | 3422 |
| 6 | x | 210 | = | 1261 | 6 | x | 420 | = | 2521 | 3782 |
| 6 | x | 231 | = | 1387 | 6 | x | 462 | = | 2773 | 4160 |
| 6 | x | 253 | = | 1519 | 6 | x | 506 | = | 3037 | 4556 |
| 6 | x | 276 | = | 1657 | 6 | x | 552 | = | 3313 | 4970 |
| 6 | x | 300 | = | 1801 | 6 | x | 600 | = | 3601 | 5402 |
| 6 | x | 325 | = | 1951 | 6 | x | 650 | = | 3901 | 5852 |
| 6 | x | 351 | = | 2107 | 6 | x | 702 | = | 4213 | 6320 |
| 6 | x | 378 | = | 2269 | 6 | x | 756 | = | 4537 | 6806 |
| 6 | x | 406 | = | 2437 | 6 | x | 812 | = | 4873 | 7310 |
| 6 | x | 435 | = | 2611 | 6 | x | 870 | = | 5221 | 7832 |
| 6 | x | 465 | = | 2791 | 6 | x | 930 | = | 5581 | 8372 |
| 6 | x | 496 | = | 2977 | 6 | x | 992 | = | 5953 | 8930 |
| 6 | x | 528 | = | 3169 | 6 | x | 1056 | = | 6337 | 9506 |
| 6 | x | 561 | = | 3367 | 6 | x | 1122 | = | 6733 | 10100 |
| 6 | x | 595 | = | 3571 | 6 | x | 1190 | = | 7141 | 10712 |
| 6 | x | 630 | = | 3781 | 6 | x | 1260 | = | 7561 | 11342 |
| 6 | x | 666 | = | 3997 | 6 | x | 1332 | = | 7993 | 11990 |
| 6 | x | 703 | = | 4219 | 6 | x | 1406 | = | 8437 | 12656 |
| 6 | x | 741 | = | 4447 | 6 | x | 1482 | = | 8893 | 13340 |
| 6 | x | 780 | = | 4681 | 6 | x | 1560 | = | 9361 | 14042 |
| 6 | x | 820 | = | 4921 | 6 | x | 1640 | = | 9841 | 14762 |
| 6 | x | 861 | = | 5167 | 6 | x | 1722 | = | 10333 | 15500 |
| 6 | x | 903 | = | 5419 | 6 | x | 1806 | = | 10837 | 16256 |
| 6 | x | 946 | = | 5677 | 6 | x | 1892 | = | 11353 | 17030 |
| 6 | x | 990 | = | 5941 | 6 | x | 1980 | = | 11881 | 17822 |
| 6 | x | 1035 | = | 6211 | 6 | x | 2070 | = | 12421 | 18632 |
| 6 | x | 1081 | = | 6487 | 6 | x | 2162 | = | 12973 | 19460 |
| 6 | x | 1128 | = | 6769 | 6 | x | 2256 | = | 13537 | 20306 |
| 6 | x | 1176 | = | 7057 | 6 | x | 2352 | = | 14113 | 21170 |
| 6 | x | 1225 | = | 7351 | 6 | x | 2450 | = | 14701 | 22052 |
| 6 | x | 1275 | = | 7651 | 6 | x | 2550 | = | 15301 | 22952 |
| www.osfantasticosnumerosprimos.com.br | ||||||||||
A tabela a seguir apresenta os 50 primeiro números triangulares gerados de números retangulares divididos por 2, retangulares estes que foram gerados conforme explanações anteriores.
Importante observar que os números retangulares também podem ser gerados por produtos de números consecutivos.
Importante notar também que tanto os números consecutivos, os números retangulares como os números triangulares gerados com os métodos apresentados neste estudo não apresentam números múltiplos de 3.
| Números | ||||
| Triangulares | ||||
| números | retangulares | triangulares | ||
| consecutivos | ||||
| soma | divisão | |||
| produtos | por 2 | |||
| 4 | x | 5 | 20 | 10 |
| 7 | x | 8 | 56 | 28 |
| 10 | x | 11 | 110 | 55 |
| 13 | x | 14 | 182 | 91 |
| 16 | x | 17 | 272 | 136 |
| 19 | x | 20 | 380 | 190 |
| 22 | x | 23 | 506 | 253 |
| 25 | x | 26 | 650 | 325 |
| 28 | x | 29 | 812 | 406 |
| 31 | x | 32 | 992 | 496 |
| 34 | x | 35 | 1190 | 595 |
| 37 | x | 38 | 1406 | 703 |
| 40 | x | 41 | 1640 | 820 |
| 43 | x | 44 | 1892 | 946 |
| 46 | x | 47 | 2162 | 1081 |
| 49 | x | 50 | 2450 | 1225 |
| 52 | x | 53 | 2756 | 1378 |
| 55 | x | 56 | 3080 | 1540 |
| 58 | x | 59 | 3422 | 1711 |
| 61 | x | 62 | 3782 | 1891 |
| 64 | x | 65 | 4160 | 2080 |
| 67 | x | 68 | 4556 | 2278 |
| 70 | x | 71 | 4970 | 2485 |
| 73 | x | 74 | 5402 | 2701 |
| 76 | x | 77 | 5852 | 2926 |
| 79 | x | 80 | 6320 | 3160 |
| 82 | x | 83 | 6806 | 3403 |
| 85 | x | 86 | 7310 | 3655 |
| 88 | x | 89 | 7832 | 3916 |
| 91 | x | 92 | 8372 | 4186 |
| 94 | x | 95 | 8930 | 4465 |
| 97 | x | 98 | 9506 | 4753 |
| 100 | x | 101 | 10100 | 5050 |
| 103 | x | 104 | 10712 | 5356 |
| 106 | x | 107 | 11342 | 5671 |
| 109 | x | 110 | 11990 | 5995 |
| 112 | x | 113 | 12656 | 6328 |
| 115 | x | 116 | 13340 | 6670 |
| 118 | x | 119 | 14042 | 7021 |
| 121 | x | 122 | 14762 | 7381 |
| 124 | x | 125 | 15500 | 7750 |
| 127 | x | 128 | 16256 | 8128 |
| 130 | x | 131 | 17030 | 8515 |
| 133 | x | 134 | 17822 | 8911 |
| 136 | x | 137 | 18632 | 9316 |
| 139 | x | 140 | 19460 | 9730 |
| 142 | x | 143 | 20306 | 10153 |
| 145 | x | 146 | 21170 | 10585 |
| 148 | x | 149 | 22052 | 11026 |
| 151 | x | 152 | 22952 | 11476 |
| www.osfantasticosnumerosprimos.com.br | ||||
Autor: Ricardo Silva - junho/2023
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos
FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.
Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato
