


Ternos Pitagóricos são sequências de 3 números inteiros que têm relação com o Teorema de Pitágoras que diz que: "O quadrado da hipotenusa é igual a soma dos quadrados dos catetos" ou "A soma dos quadrados dos catetos é igual a hipotenusa" representado pela seguinte fórmula:
a² = b² + c²
Há diversos métodos algébricos e aritméticos de se gerarem ternos pitagóricos, como também, a partir de dispositivos numéricos como a Tabuada de Multiplicação, Triângulo de Fibonacci / Haruo Hosoya, Algoritmo Escada de
Theon e Quadrados Mágicos.
Para mais informações, veja materias relacionadas abaixo.
Conforme estudo publicado no livro Digital Quadrados Mágicos e Sequências numéricas, analises realizadas nos métodos de construções de Yang Hui, Ibn Al–Hay-tham [1] e de um outro método de autor desconhecido [1] para Quadrados Mágicos de ordem ímpar, constatou-se que estes métodos apresentam semelhanças construtivas nas disposições de números tanto nas diagonais quanto nos restantes das células dos quadrados mágicos, semelhanças estas que possibilitaram a criação do Método Múltiplos em Diagonal (MD) e de uma variante do Método Simom de La Loubère, a criação do Método Múltiplos de Linha (ML).
Diferentemente de Quadrados Mágicos construídos especificamente com sequências originadas de ternos pitagóricos e seus ternos derivados, Quadrados Mágicos Normal, Puro ou Elementar, isto é, Quadrados Mágicos construídos com sequências numéricas de 1 a n² e tendo como base a configuração do Quadrado Mágico Lo-Shu são possíveis também de extrairem ternos pitagóricos, pois o terno pitagórico referente a própria ordem do quadrado aparece "embutido" no quadrado mágico.
Esta propriedade foi descoberta pelo Dr. Robert Dickter (DDS) e publicada em seu WebSite:
www.luo-shu.com
e também divulgada em outubro de 2009 no WebSite:
http://www.magic-squares.net/square-update.htm
Observação: infelizmente, os WebSites não estão mais na Word Wide Web.
O aparecimento do Quadrado Mágico têm como origem a China, e se encontra documentado no Livro Os 9 capítulos da arte matemática no texto Shu Shu Shi Yu, baseado na estória do Imperador Yu que viu sair do Rio Lo (Rio Amarelo) uma tartaruga com marcas em formas de nós feitos em barbantes sobre seu casco.
O imperador Yu também observou que as marcas quando contadas nas horizontais, verticais e diagonais possuiam uma mesma soma, isto é, 15. A partir destes eventos a tartagura, que é um animal venerado pela sua longevidade na cultura chinesa, recebeu o nome de Lo-Shu e passou a ter carater místico e esotérico.
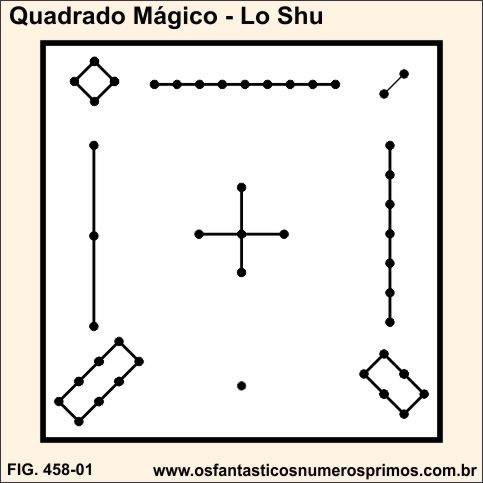
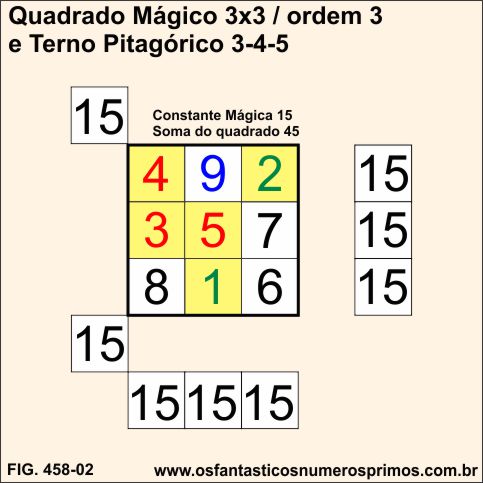
Quadrado Mágico 3x3 transcrito em numerais indo-arábicos conforme configuração do Quadrado Mágico Lo-Shu.
O número 5 na célula central do quadrado mágico é também o terceiro termo do terno pitagórico 3-4-5.
Os números 3 e 4 adjacentes a célula central são o primeiro e segundo termos do terno pitagórico 3-4-5.
A células contendo os números 3-4-5 formam um triângulo.
O quadrado de 3, o 9, aparece acima da célula central do quadrado mágico.
Os números consecutivos 1 e 2 somados, é a ordem do quadrado, bem como, os termos que formam o Terno Pitagórico 3-4-5 utilizando as Fórmulas de Euclides.
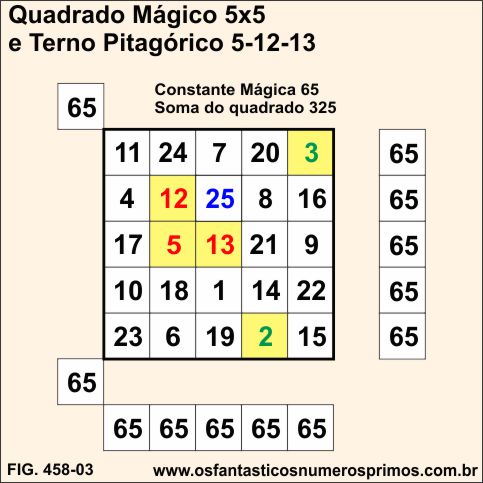
O número 13 na célula central do quadrado mágico é também o terceiro termo do terno pitagórico 5-12-13.
Os números 5 e 12 adjacentes a célula central são o primeiro e segundo termos do terno pitagórico 5-12-13.
A células contendo os números 5-12-13 formam um triângulo.
O quadrado de 5, o 25, aparece acima da célula central do quadrado mágico.
Os números consecutivos 2 e 3 somados, é a ordem do quadrado, bem como, os termos que formam o Terno Pitagórico 5-12-13 utilizando as Fórmulas de Euclides.
O número 25 na célula central do quadrado mágico é também o terceiro termo do terno pitagórico 7-24-25.
Os números 7 e 24 adjacentes a célula central são o primeiro e segundo termos do terno pitagórico 7-24-25.
A células contendo os números 7-24-25 formam um triângulo.
O quadrado de 7, o 49, aparece acima da célula central do quadrado mágico.
Os números consecutivos 3 e 4 somados, é a ordem do quadrado, bem como, os termos que formam o Terno Pitagórico 7-24-25 utilizando as Fórmulas de Euclides.

O número 41 na célula central do quadrado mágico é também o terceiro termo do terno pitagórico 9-40-41.
Os números 9 e 40 adjacentes a célula central são o primeiro e segundo termos do terno pitagórico 9-40-41.
A células contendo os números 9-40-41 formam um triângulo.
O quadrado de 9, o 81, aparece acima da célula central do quadrado mágico.
Os números consecutivos 4 e 5 somados, é a ordem do quadrado, bem como, os termos que formam o Terno Pitagórico 9-40-41 utilizando as Fórmulas de Euclides.
Observação: no Quadrado Mágico 9x9 aparece o Terno Pitagórico Primitivo 11-60-61.

Autor: Ricardo Silva - agosto/2023
[ 1 ] ARSIE, Karla Cristiane. Jogos Sudoku e Quadrado Mágico. Monografia. 2010. Universidade Federal do Paraná, Curitiba
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato