


Assim é o enunciado do Teorema de Pitágoras: "O quadrado da hipotenusa é igual a soma dos quadrados dos catetos" , ou, "A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa".
O Teorema de Pitágoras está intrisicamente relacionado a figura geométrica do triângulo retângulo escaleno.
Diversas são as demonstrações do Teorema de Pitágoras e um dos estudiosos que se "prontificou" a colecionar e a catalogar demonstrações do Teorema de Pitágoras foi o Professor de Matemática, Elisha Scott Loomis, Cleveland, Ohaio - EUA, em sua obra The Pythagorean Propositions.
Na obra de Elisha Scott Loomis, edição digital de 1968, página 100, exemplo 2, se encontra a demonstração geométrica do Teorema de Pitágoras, creditadas à Revista School Visitor de 1882, volume III, a Beman and Smiths Row´s - 1905 e a F.C. Boon.

Sintetizando os procedimentos:
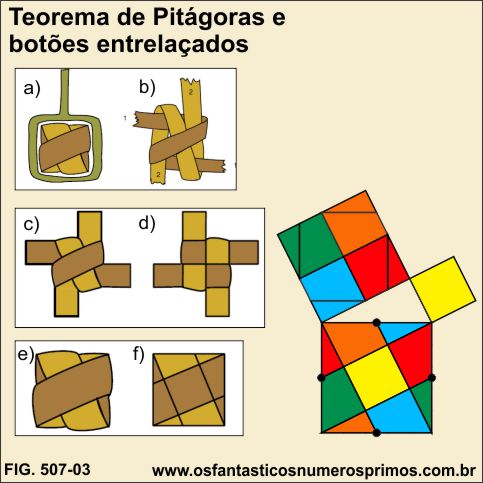
a) pegue 4 quadrados iguais ao quadrado 9 (EL);
b) a partir do ponto médio de um dos lados do quadrado, trace um seguimento até um dos vértices, desta forma se obtêm 4 triângulos retângulos e 4 trapézios;
c) com os 4 triângulos retângulos e os 4 trapézios forma-se um outro quadrado maior cujo lado corresponde à hipotenusa e o quadrado no centro cujo lado corresponde ao cateto menor.
a) a partir de um quadrado maior, trace seguimentos do ponto médio dos lados até os vértices, desta forma se obtêm 4 triângulos retângulos, 4 trapézios e um quadrado menor;
b) deslizando-se para cima, os 4 triângulos retângulos, bem como, os 4 trapézios e o quadrado menor, demonstra-se o Teorema de Pitágoras.
c) o quadrado maior corresponde à hipotenusa, o quadrado "médio" ao cateto maior e o quadrado menor ao cateto menor de um triângulo retângulo escaleno.

a) a partir de um quadrado maior dividido em 9 células, trace diagonais por 2 vértices opostos de cada grupo de 2 células, desta forma se obtêm 4 triângulos retângulos, 4 trapézios e um quadrado menor;

Em sua obra: Pitágoras Africano: Um estudo em cultura e educação matemática, edição de 2011, Paulus Pierre Joseph Gerdes (1952-2014), matemático, físico, antropólogo holandês demonstra que estudos realizados em objetos, bem como, artesanatos africanos apresentam subjacentes em suas formas o Teorema de Pitágoras.
Entrelaçando duas fitas de cores diferentes em um botão quadrado, que serve de fechamento a tampa de cesto, construída no Sul de Moçambique, a sua forma final f) se encontra "embutido" o Teorema de Pitágoras.
A forma final f) também se assemelha à Demonstração do Teorema de Pitágoras creditadas à Revista School Visitor de 1882, volume III, a Beman and Smiths Row´s - 1905 e a F.C. Boon publicada na obra The Pythagorean Propositions, conforme análises realizadas pelo WebSite Os Fantáticos Números Primos.
Mais informações, veja abaixo, Matérias Relacionadas!
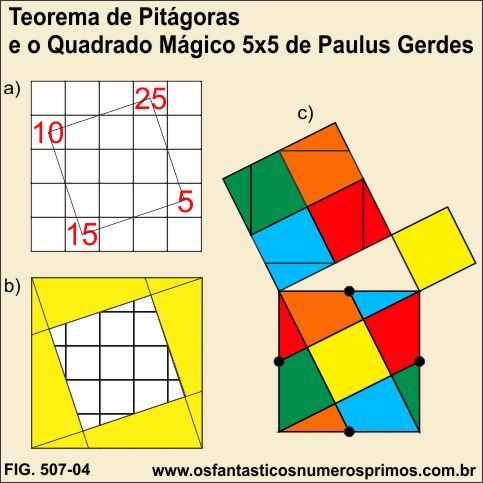
No Quadrado Latino, bem como, no Quadrado Mágico 5x5 de Paulus Gerdes, as células, onde estão os múltiplos de 5, formam vértices de um quadrado inscrito.
Prolongando-se os lados desse quadrado inscrito, o desenho geométrico final se assemelha à Demonstração do Teorema de Pitágoras creditadas à Revista School Visitor de 1882, volume III, a Beman and Smiths Row´s - 1905 e a F.C. Boon publicada na obra The Pythagorean Propositions, conforme análises realizadas pelo WebSite Os Fantáticos Números Primos.
Análises e comparações estas que devem ter passadas desapercebidas pelo Professor Paulus Gerdes em relação ao seu método de construção de quadrados mágicos, os quais tem como base artesanatos africanos.
Mais informações, veja abaixo, Matérias Relacionadas!
Autor: Ricardo Silva - julho/2024
GERDES, Paulus, Pitágoras Africano: Um estudo em cultura e educação matemática, edição digital, 2011.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato