


Quadrado Latino é uma matriz que pode ser construída por números, letras ou outros tipos de símbolos de forma que em cada linha e em cada coluna ocorra uma só vez e não podendo haver repetição dos mesmos.
Exemplo clássico originado de Quadrado Latino é o popular passatempo Sudoku em que se tem que escrever números de 1 a 9 em uma matriz quadriculada formada por 9 quadrados de 3x3 células sem que haja repetição desses mesmos números em linhas e colunas.
Quadrados Mágicos são também matrizes que podem ser formadas por progressões aritméticas, progressões geometricas e outros tipos de sequências numéricas de forma que a soma ou a multiplicação dos números de cada linha, cada coluna e diagonais apresentam um mesmo resultado o qual é denominado de Constante Mágica.
Conforme estórias e lendas chinesas de mais de 2.800 anos a.C, surgiu das águas do Rio Lo uma tartagura com marcas em seu casco em formato de Quadrado Mágico e que posteriormente foi denominado de Lo-Shu.
O Método Hindu de construção de Quadrados Mágicos tem registros nos manuscritos do sufi Ahmad bin Ali Al-buni por volta do ano 1.200 d.C no Egito.
1) Quadrado auxiliar 1 - o método consiste em tomar uma sequência correspondente a ordem do quadrado, neste caso {1, 2, 3} e montá-los conforme a seguinte disposição nas células do quadrado.
| 1 | 3 | 2 |
| 3 | 2 | 1 |
| 2 | 1 | 3 |
Observação: a disposição dos números formam uma cruz e o termo central 2 está na diagonal secundária.
2) Quadrado auxiliar 2 - multiplica-se cada termo das células pela ordem do quadrado, neste caso 3, obtendo-se os múltiplos de 3 {3, 6, 9}.
| 3 | 9 | 6 |
| 9 | 6 | 3 |
| 6 | 3 | 9 |
Observação: a disposição dos números formam uma cruz e o termo central 6 está na diagonal secundária.
3) Somam-se os termos da coluna 1 do Quadrado 1 com os termos da coluna 3 do Quadrado 2;
Somam-se os termos da coluna 3 do Quadrado 1 com os termos da coluna 1 do Quadrado 2;
Somam-se os termos da coluna 2 do Quadrado 1 com os termos da coluna 2 do Quadrado 2.
| 1 + 6 | 3 + 9 | 2 + 3 |
| 3 + 3 | 2 + 6 | 1 + 9 |
| 2 + 9 | 1 + 3 | 3 + 6 |
4) Obtendo-se um Quadrado Mágico 3x3 de Constante Mágica 24.
| 24 | |||
| 7 | 12 | 5 | 24 |
| 6 | 8 | 10 | 24 |
| 11 | 4 | 9 | 24 |
| 24 | 24 | 24 | 24 |
5) Subtraindo-se a ordem do quadrado, neste caso 3, obtem-se o Quadrado Mágico Lo-Shu.
| 7 - 3 | 12 - 3 | 5 - 3 |
| 6 - 3 | 8 - 3 | 10 - 3 |
| 11 - 3 | 4 - 3 | 9 - 3 |
| 15 | |||
| 4 | 9 | 2 | 15 |
| 3 | 5 | 7 | 15 |
| 8 | 1 | 6 | 15 |
| 15 | 15 | 15 | 15 |
O Método Hindu, como se observa, é um método bastante complexo e engenhoso, e que demandou bons conhecimentos matemáticos e de lógica para se construir Quadrados Mágicos utilizando sequências de números naturais e múltiplos de um número por meio de matrizes e que são a base de métodos de construções de Quadrados Mágicos de estudiosos e matemáticos posteriores aos escritos do sufi Ahmad bin Ali Al-buni.
Intessante observar também que o Método Hindu faz extenso uso de quadrados auxiliares para se construir Quadrado Mágico.
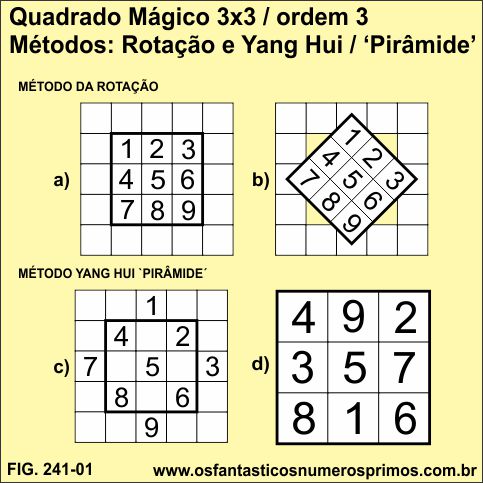
Quadrado Natural é uma matriz construída por números consecutivos de 1 a n2 e que apresentam propriedades matemáticas semelhantes a Quadrados Mágicos, estudos estes que estão publicados no livro digital Sequências Numéricas Mágicas.
A partir de um Quadrado Natural 3x3 e rotacionado-o em 45 graus, obtem-se combinações do Quadrado Mágico Lo-Shu.
A rotação do Quadrado Natural 3x3 são equivalentes aos Métodos Rotação e de Yang Hui.
O conceito de Quadrado Latino Ortogonal surge a partir de estudos realizados com Quadrados Mágicos pelo matemático Leonhard Euler.
Pares de Quadrados Latinos de mesma ordem são ortogonais se os pares ordenados correspondentes forem todos distintos, isto é, que não tenham repetição de termos.
As sequências devem obedecer as seguintes regras:
a) Quadrado-2 e Quadrado-33 deve gerar 9 pares ordenados distintos;
b) a sequência das letras latinas devem obedecer uma progressão aritmética de razão 3, resultando no tamanho da matriz;
c) a + b = 2c;
d) a sequências das letras gregas devem obedecer uma progressão geométrica de razão 1.
e) na diagonal principal de Quadrado-2, temos (a, c, b);
f) na diagonal secundária de Quadrado-3, temos (α, γ, β).
Sejam as sequências:
(a, c, b) = (1, 4, 7)
(α, γ, β) = (3, 4, 5)
e seus respectivos quadrados latinos:
Quadrado 2
| Quadrado Latino | ||
| 1 | 7 | 4 |
| 7 | 4 | 1 |
| 4 | 1 | 7 |
Quadrado 3
| Quadrado Latino | ||
| 4 | 5 | 3 |
| 3 | 4 | 5 |
| 5 | 3 | 4 |
Somando-se os os números das células correspondentes forma-se um Quadrado Latino Ortogonal...
| Quadrado Latino Ortogonal | ||
| 1 + 4 | 7 + 5 | 4 + 3 |
| 7 + 3 | 4 + 4 | 5 + 1 |
| 4 + 5 | 1 + 3 | 7 + 4 |
... e obtem-se o seguinte Quadrado Mágico de Constante Mágica 24.
| Quadrado Mágico | ||
| 5 | 12 | 7 |
| 10 | 8 | 6 |
| 9 | 4 | 11 |
Subtraindo-se 3 (ordem do Quadrado Mágico)...
| 5 - 3 | 12 - 3 | 7 - 3 |
| 10 - 3 | 8 - 3 | 6 - 3 |
| 9 - 3 | 4 - 3 | 11 - 3 |
...obtem-se uma variante do Quadrado Mágico Lo-Shu.
| Variante do Quadrado Mágico Lo-shu | ||
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
A partir do Quadrado Mágico Lo-Shu, neste exemplo, contruído com o Método de Simom de La Loubère pode-se obter Quadrados Latinos Ortogonais.
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
1) Subtraia 1 (uma unidade) de cada número do quadrado;
| 8 - 1 | 1 - 1 | 6 - 1 |
| 3 - 1 | 5 - 1 | 7 - 1 |
| 4 - 1 | 9 - 1 | 2 - 1 |
2) Obtem-se as diferenças correspondentes;
| 7 | 0 | 5 |
| 2 | 4 | 6 |
| 3 | 8 | 1 |
3) Cada diferença obtida, escreva-a na forma (3 x a) + b,
onde
0 ≤ a ≤ 2
e
0 ≤ b ≤ 2;
| (3 x 2) + 1 = 7 | (3 x 0) + 0 = 0 | (3 x 1) + 2 = 5 |
| (3 x 0) + 2 = 2 | (3 x 1) + 1 = 4 | (3 x 2) + 0 = 6 |
| (3 x 1) + 0 = 3 | (3 x 2) + 2 = 8 | (3 x 0) + 1 = 1 |
4) Obtendo-se assim Quadrados Latinos Ortogonais com seus respectivos termos da expressão (3 x a) + b, temos:
a =
| 2 | 0 | 1 |
| 0 | 1 | 2 |
| 1 | 2 | 0 |
b =
| 1 | 0 | 2 |
| 2 | 1 | 0 |
| 0 | 2 | 1 |
Há diversos métodos de construções de Quadrados Mágicos, tanto desenvolvidos por entusiastas matemáticos como por matemáticos profissionais, alguns desses métodos são apresentados aqui no WebSite Os Fantásticos Números Primos.
Os métodos demonstrados aqui no WebSite possuem uma característica em comum, uns necessitam de quadrados auxiliares e outros de quadrados auxiliares com expressões numéricas ou algébricas para se construirem Quadrados Mágicos, sejam de ordem ímpar ou ordem par.
O livro digital Quadrados Mágicos e Sequências Numéricas discorre sobre o Método Múltiplos em Diagonal e o Método Múltiplos em Linha para se construirem Quadrados Mágicos e Quadrados Semi-Magicos de ordem ímpar de forma direta, sem a necessidade de se utilizar quadrados auxiliares ou expressões numéricas ou algébricas.
Autor: Ricardo Silva - dezembro /2019
SANTOS, Cristiane Aparecida dos. Quadrados Latinos : Um estudo histórico-filosófico da matemática / Cristiane Aparecida dos Santos; Orientador, Prof. Dr. Jorge Luiz Deolindo Silva; Coorientador, Prof. Dr. Julio Faria Corrêa - Blumenau, 20:04, 4 de dezembro de 2018.
FARIAS, Fausto Gustavo. Quadrados Latinos e Quadrados Mágicos - Uma proposta didática. Dissertação de Mestrado. Universidade Federal da Paraíba Centro de Ciências Exatas e da Natureza Departamento de Matemática, 2017.
ROUSE BALLl, WW. Mathematical Recreation and Essays. Nova York, edição digital, 1905 - Gutenberg Project, 2008
BORKOVITZ, Debra K. e HWANG, Frank K. M. Discrete Mathematics
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

NOVO LIVRO DIGITAL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato