


“QUEM OUSAR BRINCAR COM NÚMEROS DESCOBRIRÁ PROPRIEDADES FASCINANTES”, frase de autoria do Professor da USP, Luiz Barco publicada na matéria da revista Superinteressante “A INESGOTÁVEL FONTE DOS NÚMEROS PRIMOS”, frase esta que não me cansarei de citá-la.
Com pesquisas feitas sobre Quadrados Mágicos, fiquei sabendo entre outras coisas:
* que Quadrados Mágicos surgiram há mais de 2.800 anos antes de Cristo na antiga China;
* que Matemáticos de renome como: Pierre de Fermat (cubo mágico tridimensional), Leonhard Euler (Quadrados Latinos), Edouard Lucas (criador do jogo matemático Torre de Hanoi), Benjamin Franklin, etc... se dedicaram à matemática recreativa;
* que os brasileiros: Lidio Machado Bandeira de Melo - jurista e professor escreveu os livros Quadrados mágicos métodos gerais para a construção de quadrados mágicos (1957) - Segundo livro dos quadrados mágicos (1959) e Alcides Navarro - entusiasta matemático escreveu - Quadrados Mágicos (2005) - onde apresenta exemplos de Quadrados Mágicos construídos com várias sequências numéricas no próprio quadrado;
* que não existe um método geral para se construirem simultaneamente Quadrados Mágicos de ordens par e ímpar;
* que até os dias atuais não se conseguiu construir um Quadrado Mágico ao quadrado 3x3.
Estudos e analises sobre métodos de construções de Quadrados Mágicos me proporcionou escrever o livro digital Quadrados Mágicos e Sequências Numéricas onde são abordados dois novos métodos de construções de Quadrados Mágicos que não necessitam de quadrados auxiliares: Método Múltiplos em Diagonal e Método Múltiplos em Linha, bem como diversas matérias aqui no WebSite Os Fantásticos Números Primos.
Quadrado Mágico 3x3 construído com os 9 primeiros números naturais. Somando-se linhas, colunas e diagonais obtem-se a Constante Mágica 15.
Os 9 primeiros números naturais formam uma progressão aritmética finita.
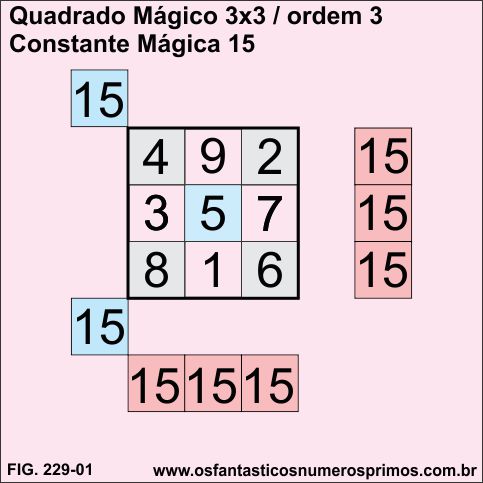
Não é possivel construir um Quadrado de quadrado 3x3 do Lo-Shu, isto é elevar seus números ao quadrado e formar um Quadrado Mágico ao quadrado, o mesmo que Quadrado Bi-Mágico, bem como com outras progressões aritméticas.
Veja matéria:
011-estudos-190-quadrados-antimagicos-3x3
| 93 | ||||
| 16 | 81 | 4 | = | 101 |
| 9 | 25 | 49 | = | 83 |
| 64 | 1 | 36 | = | 101 |
| = | = | = | ||
| 89 | 107 | 89 | 77 |
Não é possivel construir um Quadrado Mágico ao cubo do Lo-Shu, pois não forma Constante Mágica.
| 645 | ||||
| 64 | 729 | 8 | = | 801 |
| 27 | 125 | 343 | = | 495 |
| 512 | 1 | 216 | = | 729 |
| = | = | = | ||
| 603 | 855 | 567 | 405 |
9 primeiras potências de base 2:
20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
As potências de base 2 é uma progressão geométrica.
Somando-se as 9 primeiras potências de base 2 não é possivel construir Quadrado Mágico, pois não forma Constante Mágica.
| 146 | ||||
| 8 | 256 | 2 | = | 266 |
| 4 | 16 | 64 | = | 84 |
| 128 | 1 | 32 | = | 161 |
| = | = | = | ||
| 140 | 273 | 98 | 56 |
Somando-se as 9 primeiras potências de base 2 ao quadrado não é possivel construir Quadrado Mágico, pois não forma Constante Mágica.
| 16644 | ||||
| 64 | 65536 | 4 | = | 65604 |
| 16 | 256 | 4096 | = | 4368 |
| 16384 | 1 | 1024 | = | 17409 |
| = | = | = | ||
| 16464 | 65793 | 5124 | 1344 |
Multiplicando-se as 9 primeiras potências de base 2 é possivel construir Quadrado Mágico Multiplicativo de Constante Mágica 4096.
As potências de base 2 é uma progressão geométrica.
| 4096 | ||||
| 8 | 256 | 2 | = | 4096 |
| 4 | 16 | 64 | = | 4096 |
| 128 | 1 | 32 | = | 4096 |
| = | = | = | ||
| 4096 | 4096 | 4096 | 4096 |
Multiplicando-se as 9 primeiras potências de base 2 ao quadrado é possivel construir Quadrado Mágico Multiplicativo ao quadrado de Constante Mágica 16.777.216.
| 16777216 | ||||
| 64 | 65536 | 4 | = | 16777216 |
| 16 | 256 | 4096 | = | 16777216 |
| 16384 | 1 | 1024 | = | 16777216 |
| = | = | = | = | |
| 16777216 | 16777216 | 16777216 | 16777216 |
Desde a leitura da dissertação de mestrado: Estudo do quadrado mágico com uso nos anos finais do ensino fundamental onde é apresentado um exemplo de Quadrado Mágico Multiplicativo com divisores do número 36, comecei a fazer alguns questionamentos:
Como uma sequência que não é uma progressão aritmética e nem geométrica é possível construir Quadrado Mágico?
É uma sequência em que a razão não é constante, isto é, a diferença entre os termos são diferentes, semelhante a sequência de números primos.
| Divisores do | |
|---|---|
| número quadrado perfeito 36 | |
| Divisores | Diferença |
| 1 | |
| 1 | |
| 2 | |
| 1 | |
| 3 | |
| 1 | |
| 4 | |
| 2 | |
| 6 | |
| 3 | |
| 9 | |
| 3 | |
| 12 | |
| 6 | |
| 18 | |
| 18 | |
| 36 | |
| www.osfantasticosnumerosprimos.com.br | |
Construindo Quadrado Multiplicativo segundo a configuração do Lo-Shu, podendo ser utilizados os Métodos: Cruz e "Xis", Rotação e Yang Hui, a Constante Mágica falha na primeira e terceira linhas.
| Quadrado Mágico | ||||
| Multiplicativo Imperfeito 3x3 | ||||
| 216 | ||||
| 4 | 36 | 2 | = | 288 |
| 3 | 6 | 12 | = | 216 |
| 18 | 1 | 9 | = | 162 |
| = | = | = | ||
| 216 | 216 | 216 | 216 | |
veja mais informações na matéria:
011-estudos-202-quadrados-magicos-multiplicativos-divisores-de-um-numero
Será que é porque o número 36 é um quadrado e sua raiz 6 é um número perfeito e por isso que é possivel fazer Quadrado Mágico?
A partir do Quadrado Mágico "MODIFICADO" publicado na dissertação referida acima, foi construído outros quadrados em que a sequência dos divisores de 36 foram elevadas ao quadrado, ao cubo, a quarta potência, a quinta potência, etc. e sempre originando Constantes Mágicas de forma simultânea, o que não é possível fazer com uma progressão aritmética, exemplo do Quadrado Mágico Lo-Shu.
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| constante mágica 216 | ||||
| 216 | ||||
| 3 | 36 | 2 | = | 216 |
| 4 | 6 | 9 | = | 216 |
| 18 | 1 | 12 | = | 216 |
| = | = | = | ||
| 216 | 216 | 216 | 216 | |
Número Primo é um número que possui dois divisores, o número 1 e ele mesmo.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,... são exemplos de números primos.
Número Composto é o número que possui mais de dois divisores.
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24,... são exemplos de números compostos.
Número Quadrado Perfeito é um número que tem quantidade ímpar de divisores.
D(4): 1, 2, 4
3 divisores
D(9): 1, 3, 9
3 divisores
D(16): 1, 2, 4, 8, 16
5 divisores
D(25): 1, 5, 25
3 divisores
D(36): 1, 2, 3, 4, 6, 9, 12, 18, 36
9 divisores
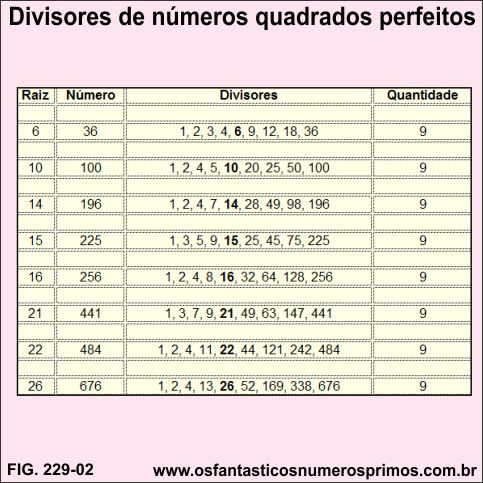
Partindo das informações sobre divisores de um número quadrado perfeito foi montada esta pequena tabela para tentar achar algun padrão em suas formações:
| Tabelas de Divisores de | |||
|---|---|---|---|
| Números Quadrados Perfeitos | |||
| Raiz | Número | Divisores | Quantidade |
| quadrado | |||
| 6 | 36 | 1, 2, 3, 4, 6, 9, 12, 18, 36 | 9 |
| 10 | 100 | 1, 2, 4, 5, 10, 20, 25, 50, 100 | 9 |
| 14 | 196 | 1, 2, 4, 7, 14, 28, 49, 98, 196 | 9 |
| 15 | 225 | 1, 3, 5, 9, 15, 25, 45, 75, 225 | 9 |
| 16 | 256 | 1, 2, 4, 8, 16, 32, 64, 128, 256 | 9 |
| 21 | 441 | 1, 3, 7, 9, 21, 49, 63, 147, 441 | 9 |
| 22 | 484 | 1, 2, 4, 11, 22, 44, 121, 242, 484 | 9 |
| 26 | 676 | 1, 2, 4, 13, 26, 52, 169, 338, 676 | 9 |
Fonte: Tabela adaptada de
https://pt.www.wikipedia.org/
1) a diferença entre uma raiz e outra não é constante;
2) a diferença entre um quadrado e outro não é constante;
3) nas raízes não há números primos;
4) os números quadrados não são quadrados de números primos;
Onde estaria o segredo, o padrão de formação das sequências dessas raízes e de seus respectivos números quadrados?
A única informação comum é a quantidade 9 de divisores, que por sinal é um número quadrado perfeito.
Outra tabela foi elaborada, intercalando-se as raízes quadradas entre os números primos.
Reparei que as raízes quadradas são números compostos e algumas pares, cujas metades são números primos, exceto a raiz 16 (opâ!! epâ!!).
A metade da raiz multiplicada por 2. (opâ!! epâ!!)
3 x 2 = 6 (produto de dois primos)
5 x 2 = 10 (produto de dois primos)
E a raízes de números compostos ímpares 15 e 21? (opâ!! epâ!!)
5 x 3 = 15 (produto de dois primos)
7 x 3 = 21 (produto de dois primos)
A raiz 16 é um número composto, quadrado de 4 e potência de base 2. (opâ!! epâ!!)
| Tabela de Números Primos | |||
|---|---|---|---|
| e Raízes Quadradas | |||
| Números Primos | Raízes Quadradas | Multiplicação de | |
| dois Primos | |||
| 2 | = | ||
| = | |||
| 3 | = | ||
| = | |||
| 5 | = | ||
| 6 | = | 3 x 2 | |
| 7 | = | ||
| 10 | = | 5 x 2 | |
| 11 | = | ||
| = | |||
| 13 | = | ||
| 14 | = | 7 x 2 | |
| 15 | = | 5 x 3 | |
| 16 | = | 8 x 2 | |
| 17 | = | ||
| = | |||
| 19 | = | ||
| 21 | = | 7 x 3 | |
| 22 | = | 11 x 2 | |
| 23 | = | ||
| 26 | = | 13 x 2 | |
| 29 | = | ||
| www.osfantasticosnúmerosprimos.com.br | |||
Elaborando os divisores das raízes quadradas...
D(6): 1, 2, 3, 6
D(10): 1, 2, 5, 10
D(14): 1, 2, 7, 14
D(15): 1, 3, 5, 15
D(16): 1, 2, 4, 8, 16 (opâ!! epâ!!) - 5 divisores
D(21): 1, 3, 7, 21
D(22): 1, 2, 11, 22
D(26): 1, 2, 11, 26
As raízes possuem 4 divisores (4 é quadrado perfeito), com exceção do 16 que é um quadrado perfeito e potência de base 2. (opâ!! epâ!!)
Com exceção do 16, multiplicando os termos centrais (números primos), obtem-se as raízes quadradas.
Tabulando algumas potências de base de números primos com as raízes quadradas de números compostos verifica-se principalmente que:
1) as raízes de números compostos não são potências de números primos (faixas amarela);
2) as raízes de números compostos são formadas por produto de dois números primos distintos;
Exemplos:
2 x 3 = 6
2 x 5 = 10
2 x 7 = 14
3) a raiz 16 é um potência de base 2 e um número quadrado perfeito, possui 5 divisores;
| Tabela de Potências | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| de Números Primos | |||||||||||
| Núm. | Número | Potência | Base | ||||||||
| Composto | |||||||||||
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |||
| 1 | |||||||||||
| 2 | p | 2 | |||||||||
| 3 | p | 3 | |||||||||
| 4 | p | 4 | |||||||||
| 5 | p | 5 | |||||||||
| 6 | c | ||||||||||
| 7 | p | 7 | |||||||||
| 8 | p | 8 | |||||||||
| 9 | p | 9 | |||||||||
| 10 | c | ||||||||||
| 11 | p | 11 | |||||||||
| 12 | |||||||||||
| 13 | p | 13 | |||||||||
| 14 | c | ||||||||||
| 15 | c | ||||||||||
| 16 | p | 16 | |||||||||
| 17 | p | 17 | |||||||||
| 18 | |||||||||||
| 19 | p | 19 | |||||||||
| 20 | |||||||||||
| 21 | c | ||||||||||
| 22 | c | ||||||||||
| 23 | p | 23 | |||||||||
| 24 | |||||||||||
| 25 | p | 25 | |||||||||
| 26 | c | ||||||||||
| 27 | p | 27 | |||||||||
| 28 | |||||||||||
| 29 | p | ||||||||||
| 30 | |||||||||||
| 31 | p | ||||||||||
| 32 | p | 32 | |||||||||
| www.osfantasticosnúmerosprimos.com.br | |||||||||||
4) Os números 12, 18, 20, 24, 30 e outros, também não são potências de números primos e suas metades são números compostos.
Exempos:
a) Número 12
12 : 2 = 6 (6 é número composto e não é número primo)
D(12): 1, 2, 3, 4, 6, 12
possue 6 divisores (6 não um quadrado perfeito)
os termos médios 3 e 4 (um número primo e um composto)
144 - quadrado de 12 - possui 15 divisores
b) Número 18
18 : 2 = 9 (9 é número composto e não é número primo)
D(18): 1, 2, 3, 6, 9, 18
possue 6 divisores (6 não um número quadrado perfeito)
os termos médios 3 e 6 (um número primo e um composto)
324 - quadrado de 18 - possui 15 divisores
b) Número 20
20 : 2 = 10 (10 é número composto e não é número primo)
D(20): 1, 2, 4, 5, 10, 20
possue 6 divisores (6 não um quadrado perfeito)
os termos médios 4 e 5 (um número composto e um primo)
400 - quadrado de 20 - possui 15 divisores
O número base 3 é um número primo.
Nas potências de base 3, cada número posterior é o triplo do anterior.
As quantidades de divisores das potências de base 3 não resultam sequencialmente números em quantidade de números quadrados perfeitos.
Com as potências de base de números primos não são possíveis de se gerarem Quadrados Mágicos Multiplicativos simultaneamente.
30 = 1 (quadrado perfeito)
31 = 3
2 divisores
32 = 9 (quadrado perfeito)
3 divisores
33 = 27
4 divisores
34 = 81 (quadrado perfeito)
5 divisores
35 = 243
6 divisores
36 = 729 (quadrado perfeito)
7 divisores
37 = 2.187
8 divisores
38 = 6.561 (quadrado perfeito)
a) Todo número elevado a um expoente par tem como resultado um número quadrado perfeito.
Raiz Quadrada: 81
b) Potências de base 3 quando decompostas em fatores primos tem um único fator primo, o número 3.
Fatoração: 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 6.561
c) Todo número quadrado perfeito tem quantidades ímpares de divisores.
Quantidade de divisores: 9
Divisores de 6.561 (1, 3, 9, 27, 81, 243, 729, 2187, 6561)
39 = 19.683
10 divisores
310 = 59.049 (quadrado perfeito)
11 divisores
O número base 6 é o primeiro número composto e que não é potência de um outro número.
Nas potências de base 6, cada número posterior é o sêxtuplo do anterior.
As quantidades de divisores das potências de base 6 tem como resultados números quadrados perfeitos.
A partir da potência 36 de base 6 é possivel gerar Quadrados Mágicos Multiplicativos simultaneamente.
60 = 1 (quadrado perfeito)
61 = 6
4 divisores
62 = 36 (quadrado perfeito)
a) Todo número elevado a um expoente par tem como resultado um número quadrado perfeito.
Raiz Quadrada: 6
b) Potências de base 6 quando decompostas em fatores primos tem dois únicos fatores primos, o número 2 e 3.
Fatoração: 2 x 2 x 3 x 3 = 36
c) Todo número quadrado perfeito tem quantidades ímpares de divisores.
Quantidade de divisores: 9
Divisores: 1, 2, 3, 4, 6, 9, 12, 18, 36
63 = 216
16 divisores
64 = 1296 (quadrado perfeito)
25 divisores
65 = 7.776
36 divisores
66 = 46.656 (quadrado perfeito)
49 divisores
67 = 279.936
64 divisores
68 = 1.679.616 (quadrado perfeito)
81 divisores
69 = 10.077.696
100 divisores
610 = 60.466.176 (quadrado perfeito)
121 divisores
Potências de números primos não possuem divisores em quantidades de números quadrados perfeitos sequencialmente.
Determinados números compostos que não são potências de números primos, possuem potências cujos divisores são em quantidade de números quadrados perfeitos sequencialmente.
[1] MARQUES, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
[2] https://pt.wikipedia.org/wiki/
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
Autor: Ricardo Silva - agosto/2019

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato