


Quadrados Mágicos Anti-Mágicos, Imperfeitos ou Defeituosos 3x3 ou de ordem 3 são quadrados mágicos cujas somas de cada linha, cada coluna, bem como as diagonais não resultam em Constantes Mágicas.
Conforme o WebSite http://www.magic-squares.net, há duas denominações específicas para Quadrados Mágicos Defeituosos ou Imperfeitos:
AntiMagic Square
Quadrados Mágicos cujas somas de cada linha, cada coluna e diagonais apresentam números consecutivos.
Heterosquare
Quadrados Mágicos cujas somas de cada linha, cada colunas e diagonais são diferentes.
Quadrados Bi-Mágicos, Tri-Mágicos, Tetra-Mágicos, também denominados Multimágicos são quadrados que quando os seus números são elevados a determinada potência como ao quadrado, a terceira potência, a quarta potência e assim por diante, eles continuam mágicos.
Até os dias atuais, não se conseguiu construir Quadrado Mágico de ordem 3, que seja Bi-Mágico.
Can a 3x3 magic square be constructed with nine distinct square numbers? This short question asked by Martin LaBar in 1984 became famous when Martin Gardner republished it in 1996 and offered $100 to the first person to construct such a square. Two years later, Gardner wrote:
So far no one has come forward with a “square of squares” – but no one has proved its impossibility either. If it exists, its numbers would be huge, perhaps beyond the reach of today’s fastest computers.
Fonte: http://www.multimagie.com
Pode um quadrado mágico de 3x3 ser construído com nove números quadrados distintos? Esta pequena pergunta feita por Martin LaBar em 1984 tornou-se famosa quando Martin Gardner a republicou em 1996 e ofereceu US$ 100 para a primeira pessoa a construir tal quadrado. Dois anos depois, Gardner escreveu:
Até agora ninguém avançou com um “quadrado de quadrados” - mas ninguém provou sua impossibilidade. Se existir, seus números seriam enormes, talvez além do alcance dos computadores mais rápidos de hoje.
A partir de Quadrados Mágicos de ordem 3, formados com números consecutivos cujo o primeiro termo inicia-se com número ímpar e elevando-os a determinada potência, constroem-se Quadrados Anti-Mágicos os quais apresentam as seguintes caracterísicas:
a) as somas das linhas 1 e 3 apresentam uma mesma constante;
b) as somas das coluna 1 e 3 apresentam uma mesma constante;
c) a soma de todos os números é múltiplo de 3.
Progressão aritmética finita de 1 a 9, com o primeiro termo ímpar.
| 05 | ||||||||
| 04 | 06 | |||||||
| 03 | 07 | |||||||
| 02 | 08 | |||||||
| 01 | 09 |
Quadrado Mágico construído conforme configuração do Quadrado Mágico Lo Shu.
| Quadrado Mágico 3x3 | ||||
| Constante Mágica 15 | ||||
| 15 | ||||
| 4 | 9 | 2 | 15 | |
| 3 | 5 | 7 | 15 | |
| 8 | 1 | 6 | 15 | |
| 15 | 15 | 15 | 15 | |
Sequência de números quadrados perfeito de 1 a 81.
| 25 | ||||||||
| 16 | 36 | |||||||
| 09 | 49 | |||||||
| 04 | 64 | |||||||
| 01 | 81 |
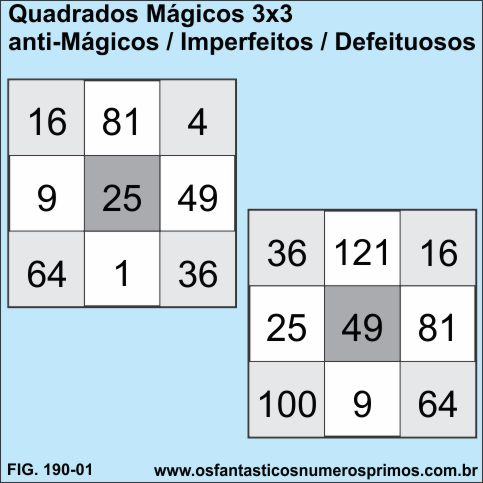
Quadrado Mágico Imperfeito construído com números quadrados pefeitos de 1 a 81.
| Quadrado Mágico 3x3 | ||||
| Imperfeito | ||||
| ao quadrado | ||||
| 93 | ||||
| 16 | 81 | 4 | 101 | |
| 9 | 25 | 49 | 83 | |
| 64 | 1 | 36 | 101 | |
| 89 | 107 | 89 | 77 | |
As linhas 1 e 3 apresentam uma mesma constante 101 que é um número primo.
As colunas 1 e 3 apresentam uma mesma constante 89 que é um número primo.
A linha e coluna do meio tem como resultados números primos: 83 e 107.
A soma de todos os números: 285 é um múltiplo de 3.
Progressão aritmética finita de 3 a 11, com o primeiro termo ímpar.
| 07 | ||||||||
| 06 | 08 | |||||||
| 05 | 09 | |||||||
| 04 | 10 | |||||||
| 03 | 11 |
Quadrado Mágico construído conforme configuração do Quadrado Mágico Lo Shu.
| Quadrado Mágico 3x3 | ||||
| Constante Mágica 21 | ||||
| 21 | ||||
| 6 | 11 | 4 | 21 | |
| 5 | 7 | 9 | 21 | |
| 10 | 3 | 8 | 21 | |
| 21 | 21 | 21 | 21 | |
Sequência de números quadrados perfeito de 9 a 121.
| 49 | ||||||||
| 36 | 64 | |||||||
| 25 | 81 | |||||||
| 16 | 100 | |||||||
| 09 | 121 |
Quadrado Mágico Imperfeito construído com números quadrados pefeitos de 9 a 121.
| Quadrado Mágico 3x3 | ||||
| imperfeito | ||||
| ao quadrado | ||||
| 165 | ||||
| 36 | 121 | 16 | 173 | |
| 25 | 49 | 81 | 155 | |
| 100 | 9 | 64 | 173 | |
| 161 | 179 | 161 | 149 | |
As linhas 1 e 3 apresentam uma mesma constante 173 que é um número primo.
As colunas 1 e 3 apresentam uma mesma constante 161 que é não um número primo.
A diagonal principal tem como resultado 149 que é número primo.
A soma de todos os números: 501 é um múltiplo de 3.
Progressão aritmética finita de 5 a 13, com o primeiro termo ímpar.
| 09 | ||||||||
| 08 | 10 | |||||||
| 07 | 11 | |||||||
| 06 | 12 | |||||||
| 05 | 13 |
Quadrado Mágico construído conforme configuração do Quadrado Mágico Lo Shu.
| Quadrado Mágico 3x3 | ||||
| Constante Mágica 27 | ||||
| 27 | ||||
| 8 | 13 | 6 | 27 | |
| 7 | 9 | 11 | 27 | |
| 12 | 5 | 10 | 27 | |
| 27 | 27 | 27 | 27 | |
Sequência de números quadrados perfeito de 9 a 121.
| 81 | ||||||||
| 64 | 100 | |||||||
| 49 | 121 | |||||||
| 36 | 144 | |||||||
| 25 | 169 |
Quadrado Mágico Imperfeito construído com números quadrados pefeitos de 25 a 169.
| Quadrado Mágico 3x3 | ||||
| Imperfeito | ||||
| ao quadrado | ||||
| 261 | ||||
| 64 | 169 | 36 | 269 | |
| 49 | 81 | 121 | 251 | |
| 144 | 25 | 100 | 269 | |
| 257 | 275 | 257 | 245 | |
As linhas 1 e 3 apresentam uma mesma constante 269 que é um número primo.
As colunas 1 e 3 apresentam uma mesma constante 257 que é um número primo.
A soma de todos os números: 789 é um múltiplo de 3.
Nos exemplos a seguir são apresentados Quadrados Mágicos Imperfeitos de ordem 3 ao cubo originados de cada uma das progressões aritméticas finitas acima.
Os quadrados não apresentam Constantes Mágicas e Somas Mágicas
A soma de cada coluna, cada linha, cada diagonal, bem como a soma de todos os números de cada quadrado é múltiplo de 3.
| Quadrado Mágico 3x3 | ||||
| Impefeito | ||||
| ao cubo | ||||
| 645 | ||||
| 64 | 729 | 8 | 801 | |
| 27 | 125 | 343 | 495 | |
| 512 | 1 | 216 | 729 | |
| 603 | 855 | 567 | 405 | |
| Quadrado Mágico 3x3 | ||||
| Impefeito | ||||
| ao cubo | ||||
| 1407 | ||||
| 216 | 1331 | 64 | 1611 | |
| 125 | 343 | 729 | 1197 | |
| 1000 | 27 | 512 | 1539 | |
| 1341 | 1701 | 1305 | 1071 | |
| Quadrado Mágico 3x3 | ||||
| Impefeito | ||||
| ao cubo | ||||
| 2673 | ||||
| 512 | 2197 | 216 | 2925 | |
| 343 | 729 | 1331 | 2403 | |
| 1728 | 125 | 1000 | 2853 | |
| 2583 | 3051 | 2547 | 2241 | |
Autor: Ricardo Silva - julho/2018
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato