Página de estudos de matemática e sequências numéricas

Quadrados Mágicos e divisores de um número natural - 210

Quadrados Mágicos são dispositivos numéricos construídos com quadrados quadriculados cujas quantidades de células são em números de quadrados perfeitos nas quais números são dispostos em certa ordem de forma que a somas de cada linha, cada coluna e diagonais tenham um mesmo resultado, chamada de Constante Mágica.

Quadrados Mágicos são classificados das seguintes formas:

Quadrados Mágicos 3x3 ou de ordem 3 - possuem 9 células (3²).

Quadrados Mágicos 4x4 ou de ordem 4 - possuem 16 células (4²).

Quadrados Mágicos 5x5 ou de ordem 5 - possuem 25 células (5²) e assim sucessivamente.

Quadrado Mágico 3x3 ou de ordem 3 - Lo-Shu

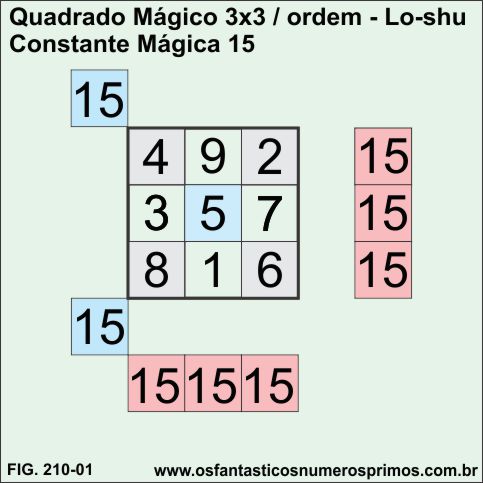
Quadrado Mágico 3x3 construído com os 9 primeiros números naturais de Constante Mágica 15 é chamado de Lo-Shu

Até os dias atuais, não se sabe se é possivel construir um Quadrado de quadrado do Lo-Shu, isto é elevar seus números ao quadrado e formar um Quadrado Mágico ao quadrado, o mesmo que Quadrado Bi-Mágico.

Conforme estudos publicado aqui no site:

011-estudos-190-quadrados-antimagicos-3x3

também não foi possível construir um Quadrado Mágico ao cubo.

Quadrados Mágicos podem ser construídos com progressões aritméticas, progressões geométricas e também com sequências numéricas em que necessariamente não precisa haver uma constante entre os seus termos.

A sequência numérica dos divisores do número 36, por exemplo não há uma constante entre seus termos, isto é, uma razão:

D (36): 1, 2, 3, 4, 6, 9, 12, 18, 36.

A potência de 6, 36 que é um número quadrado perfeito e seus divisores, como outros números analisados até o presente momento, apresentam uma propriedade que os diferem de outras potências originadas de números primos.

Determinadas potências, como as potências dos números compostos 6, 10, 14 e outras começando pelos seus quadrados perfeitos têm quantidades de divisores em números quadrados perfeitos e que são justamente as quantidades com as quais são construídas Quadrados Mágicos.

Sequência de Fibonacci

Assim como os números da Sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... aumentam rapidamente, com as Potências dos números naturais também acontece o mesmo.

Números de Fibonacci:

O 50⁰ número de Fibonacci é:

12.586.269.025;

O 100⁰ número de Fibonacci é:

354.224.848.179.261.915.075.

Potenciação

Potenciação e a operação matemática que utilizamos para indicar uma multiplicação de fatores iguais.

2³ = 2 x 2 x 2 = 8

onde:

2 é a base

3 é o expoente

8 é a potência

Potências de base 2

Nas potências de base 2, cada potência posterior é o dobro da potência anterior.

2⁰ = 1

2¹ = 2

2² = 2 x 2 = 4

2³ = 2 x 2 x 2 = 8

2⁴ = 2 x 2 x 2 x 2 = 16

2⁵ = 2 x 2 x 2 x 2 x 2 = 32

2⁶ = 2 x 2 x 2 x 2 x 2 x 2 = 64

2⁷ = 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128

2⁸ = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 256

Decomposição em fatores primos de potências de base 2

Na decomposição em fatores primos de potências de base 2, a quantidade de divisores é 1 unidade maior que a quantidade de fatores primos.

2 é o fator primo principal nas decomposições de potências de base 2.

A base 2 é um número primo.

Número 2

O número 2 é um número primo.

Números Primos são números que tem 2 divisores, o número 1 e ele mesmo.

D (2): {1 e 2}

Número 4 - quadrado perfeito

O número 4 é um número quadrado perfeito originado do número primo 2.

Todo número quadrado perfeito tem quantidade ímpar de divisores.

Números Quadrados Perfeitos originados de números primos possuem 3 divisores.

D (4): {1, 2, 4}

Número 8

Número 16 - quadrado perfeito

O número 16 é um número quadrado.

raiz quadrada: 4.

Todo número quadrado perfeito tem quantidade ímpar de divisores.

D (16): {1, 2, 4, 8, 16}

Número 32

Número 64 - quadrado perfeito

O número 64 é um número quadrado.

raiz quadrada: 8.

Todo número quadrado perfeito tem quantidade ímpar de divisores.

D (16): {1, 2, 4, 8, 16, 32, 64}

Número 128

Número 256 - quadrado perfeito

O número 256 é um número quadrado.

raiz quadrada: 16.

Todo número quadrado perfeito tem quantidade ímpar de divisores.

D (16): {1, 2, 4, 8, 16, 32, 64, 128, 256}

Para se construirem Quadrados Mágicos com potências de base 2, deve se escolher uma potência de base 2 cujo expoente é uma unidade menor de um número quadrado perfeito.

O divisores da potência 256 de base 2 possuem 9 divisores, portanto é possivel construir Quadrado Mágico Multiplicativo 3x3 ou de ordem 3.

Observação: os divisores de 256 formam um Progressão Geométrica (P.G.).

Potências de base 3

O número base 3 é um número primo.

Nas Potências de base 3, cada número posterior é o triplo do anterior.

Na decomposição em fatores primos de potências de base 3, a quantidade de divisores também é 1 unidade maior que a quantidade de fatores primos.

3⁰ = 1 (quadrado perfeito)

3¹ = 3 (número primo)

2 divisores

3² = 3 x 3 = 9 (quadrado perfeito)

3 divisores

3³ = 3 x 3 x 3 = 27

4 divisores

3⁴ = 3 x 3 x 3 x 3 = 81 (quadrado perfeito)

5 divisores

3⁵ = 3 x 3 x 3 x 3 x 3 = 243

6 divisores

3⁶ = 3 x 3 x 3 x 3 x 3 x 3 = 729 (quadrado perfeito)

7 divisores

3⁷ = 3 x 3 x 3 x 3 x 3 x 3 x 3 = 2.187

8 divisores

3⁸ = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 6.561 (quadrado perfeito)

a) Todo número elevado a um expoente par tem como resultado um número quadrado perfeito.

Raiz Quadrada: 81

b) Potências de base 3 quando decompostas em fatores primos tem um único fator primo, o número 3.

c) Todo número quadrado perfeito tem quantidades ímpares de divisores.

Quantidade de divisores: 9

D(6.561): {1, 3, 9, 27, 81, 243, 729, 2187, 6561}

Observação: os divisores de 6.561 formam um Progressão Geométrica (P.G.).

3⁹ = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 =19.683

10 divisores

3¹⁰ = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 59.049 (quadrado perfeito)

11 divisores

Número 6

O número 6 é o primeiro número composto e que não é potência de um outro número.

Números compostos são números que possuem mais de 2 divisores.

Potências de base 6

6⁰ = 1

6¹ = 6

6² = 6 x 6 = 36

6³ = 6 x 6 x 6 = 216

6⁴ = 6 x 6 x 6 x 6 = 1.296

6⁵ = 6 x 6 x 6 x 6 x 6 = 7.776

6⁶ = 6 x 6 x 6 x 6 x 6 x 6 = 46.656

6⁷ = 6 x 6 x 6 x 6 x 6 x 6 x 6 = 279.936

6⁸ = 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 = 1.679.616

6⁹ = 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 = 10.077.696

6¹⁰ = 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 = 60.466.176

Decomposição em fatores primos de potências de base 6

Na decomposição em fatores primos de potências de base 6, a quantidade de divisores é um número quadrado perfeito.

2 e 3 são os fatores primos principais nas decomposições de potências de base 6.

Observação: as sequências de divisores das potências de base 6 não formam progressão artimética nem geométrica, pois não possuem constante entre seus termos.

Número 6

A quantidade divisores do número 6 é 4.

4 é um número quadrado perfeito.

Número 36 - quadrado perfeito

O número 36 é um número quadrado perfeito originado do número composto 6.

Todo número quadrado perfeito tem quantidade ímpar de divisores.

Números Quadrados Perfeitos originados de números compostos possuem mais de 3 divisores.

D (36): 1, 2, 3, 4, 6, 9, 12, 18, 36.

A quantidade divisores do número quadrado perfeito 36 é 9.

9 é um número quadrado perfeito.

9 números é a quantidade para se construir Quadrado Mágico Multiplicativo 3x3 ou de ordem 3.

Número 216 - cubo perfeito

A quantidade divisores do número 216 é 16.

16 é um número quadrado perfeito.

16 números é a quantidade para se construir Quadrado Mágico 4x4, de ordem 4.

Número 1296 - quadrado perfeito

A quantidade divisores do número 1296 é 25.

25 é um número quadrado perfeito.

25 números é a quantidade para se construir Quadrado Mágico Multiplicativo 5x5 ou de ordem 5.

Número 7.776

6⁵ = 7.776

36 divisores

36 números é a quantidade para se construir Quadrado Mágico Multiplicativo 6x6 ou de ordem 6.

Número 46.656 - quadrado perfeito

6⁶ = 46.656

49 divisores

49 números é a quantidade para se construir Quadrado Mágico Multiplicativo 7x7 ou de ordem 7.

Número 279.936

6⁷ = 279.936

64 divisores

64 números é a quantidade para se construir Quadrado Mágico Multiplicativo 8x8 ou de ordem 8.

Número 1.679.616 - quadrado perfeito

6⁸ = 1.679.616

81 divisores

81 números é a quantidade para se construir Quadrado Mágico Multiplicativo 9x9 ou de ordem 9.

Número 10.077.696 - cubo perfeito

6⁹ = 10.077.696

100 divisores

100 números é a quantidade para se construir Quadrado Mágico Multiplicativo 10x10 ou de ordem 10.

Número 60.466.176 - quadrado perfeito

6¹⁰ = 60.466.176

121 divisores

121 números é a quantidade para se construir Quadrado Mágico Multiplicativo 11x11 ou de ordem 11.

Conclusão:

Nos estudos aqui apresentados são demonstrados novas propriedades numéricas relacionadas a determinados números compostos de que suas potências possuem divisores em quantidade de números quadrados perfeitos.

[1] Tabela adaptada de:

https://pt.wikipedia.org/wiki/Tabela_de_divisores

Autor: Ricardo Silva - novembro/2018

Fontes Bibliográficas:

[1] https:// pt.wikipedia.org/wiki/Tabela_de_divisores

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

Matérias relacionadas:

011-estudos-095-divisores-de-um-numero-suas-regularidades-numericas

011-estudos-202-quadrados-magicos-multiplicativos-divisores-de-um-numero

011-estudos-203-quadrados-magicos-multiplicativos-e-divisores-de-36

011-estudos-204-quadrados-magicos-multiplicativos-e-divisores-de-100

011-estudos-205-quadrados-semi-magicos-multiplicativos-4x4

011-estudos-206-quadrados-semi-magicos-multiplicativos-5x5

011-estudos-207-quadrados-magicos-divisores-de-numeros-quadrados-perfeitos

011-estudos-227-quadrados-magicos-sequencia-fibonacci

NOVO LIVRO DIGITAL (E-book)

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Quadrado Mágico Triplo

DOWNLOAD GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.