capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Quadrados Mágicos e Sequência de Fibonacci - 227

Assim como o Teorema de Pitágoras que tem diversas aplicações em ramos da Matemática e das Ciências e inclusive dezenas de demonstrações compiladas no livro The Pythagorean Propositions do Professor estadunidense Elisha Scott Loomis, reimpressão da segunda edição de 1940, com a Sequência de Fibonacci não é diferente, pois é uma sequência numérica que possui diversas propriedades aritméticas, algébricas e geométricas, algumas publicadas aqui no WebSite.

A Sequência de Fibonacci está relacionada com a biologia, com a fauna, com a flora, com o cosmos e possui organizações que se dedicam esclusivamente aos estudos de suas propriedades.

quadrado mágico 3x3 imperfeito de Fibonacci

Quadrados Mágicos são dispositivos numéricos formados por células quadriculadas em quantidade de números quadrados perfeitos nas quais os números são dispostos em certa ordem e tem como resultado a soma de cada linha, cada coluna e diagonais o mesmo resultado e que é denominado de Constante Mágica.

Há quadrados formados por 9 células (3x3), 16 células (4x4), 25 células (5x5) e assim por diante.

Quadrados Mágicos e sequências numéricas

Quadrados Mágicos podem ser construídos com:

progressões aritméticas;

progressões geométricas;

números consecutivos pares;

números consecutivos ímpares;

números primos;

frações;

raízes quadradas;

desenhos;

símbolos;

divisores de um número natural, etc.

Quadrado Natural 3x3 / Quadrado de Números Consecutivos

Quadrado Natural ou Quadrado de Números Consecutivos são formados por sequências finitas de números consecutivos.

Estudos desses quadrados estão publicados no livro digital Sequência Numéricas Mágicas e demonstram que suas construções estão amplamente relacionadas, entre outras, com sequências de números triangulares, números quadrados perfeitos, etc.

No Quadrado Natural formado pelos 9 primeiros números naturais, as somas da coluna central, linha central e diagonais tem como resultado 15.

Todas as somas são múltiplos de 3.

Quadrado Natural
de números consecutivos
			15
1	2	3	6
4	5	6	15
7	8	9	24
12	15	18	15

Quadrado Mágico 3x3 - Lo-shu

Quadrado Mágico Lo-Shu é o primeiro quadrado mágico formado por progressão aritmética finita de 9 termos (1, 2, 3, 4, 5, 6, 7, 8, 9).

Constante Mágica 15.

Quadrado Mágico
3x3 - Lo-Shu
constante mágica 15
			15
4	9	2	15
3	5	7	15
8	1	6	15
15	15	15	15

Quadrado Mágico Multiplicativo Imperfeito 3x3 - Lo-shu

Quadrado multiplicativo é o quadrado em que os termos de cada linha, cada coluna e diagonais são muliplicados.

Com a progressão aritmética finita de 9 termos (1, 2, 3, 4, 5, 6, 7, 8, 9) não é possível construir um Quadrado Mágico Multiplicativo Perfeito, pois não se forma Constante Mágica.

Quadrado Mágico
Multiplicativo Imperfeito 3x3
			80

4	9	2	72
3	5	7	105
8	1	6	48

96	45	84	120

A soma das linhas e a soma das colunas têm os mesmos resultados: 225.

Quadrado Natural Imperfeito 3x3 - divisores de 36

Com sequência numérica de 9 termos dos múltiplos de 36 (1, 2, 3, 4, 6, 9, 12, 18 é 36) é não é possível construir um Quadrado Natural Perfeito, pois nem todas as somas são múltiplos de 6.

Quadrado Mágic
o Imperfeito 3x3

			21

1	2	3	6
4	6	9	19
12	18	36	66

17	26	48	43

Quadrado Mágico 3x3 - divisores de 36

Com sequência numérica de 9 termos dos múltiplos de 36 (1, 2, 3, 4, 6, 9, 12, 18 é 36) é não é possível construir um Quadrado Mágico Perfeito, pois não se forma Constante Mágica.

Quadrado Mágico
Imperfeito 3x3
			26

4	36	2	42
3	6	12	21
18	1	9	28

25	43	23	19

Quadrado Mágico Multiplicativo Perfeito 3x3

Quadrado Mágico Multiplicativo é o quadrado em que os termos de cada linha, cada coluna e diagonais são multiplicados.

A Constante Mágica é o produto dos termos.

Com sequência numérica de 9 termos dos múltiplos de 36 (1, 2, 3, 4, 6, 9, 12, 18 é 36) é possível construir um Quadrado Mágico Multiplicativo Perfeito, pois se forma Constante Mágica.

Observação importante: sequências de divisores de um número natural não formam progressões aritméticas e nem progressões geométricas.

Divisores do
número quadrado perfeito 36

Número	Diferença

1
	1
2
	1
3
	1
4
	2
6
	3
9
	3
12
	6
18
	18
36

www.osfantasticosnumerosprimos.com.br

Quadrado Mágico
Multiplicativo 3x3
constante mágica 216
			216

3	36	2	216
4	6	9	216
18	1	12	216

216	216	216	216

Quadrado Natural Imperfeito 3x3 - Fibonacci

A Sequência de Fibonacci é formada repetindo-se o número 1 duas vezes e somando-se dois números anteriores:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,...

A Sequência de Fibonacci também não é uma progressão aritmética e nem progressão geométrica, mas possui diversas propriedades matemáticas, numéricas, geométricas, etc...

Com a sub-sequência 1, 2, 3, 5, 8, 13, 21, 34 e 55 de números de Fibonacci não foi possível construir um Quadrado Natural pois as somas de cada uma das colunas, linhas e diagonais apresentam resultados diferentes.

Quadrado Natural
Imperfeito 3x3
de Fibonacci
			32
1	2	3	6
5	8	13	26
21	34	55	110
27	44	71	64

Quadrado Mágico Imperfeito 3x3 - Fibonacci

Vejamos algumas sub-sequências utilizadas em Quadrados Mágicos.

Sequência de 9 números de Fibonacci

A diferença entre cada termo da sequência dos 9 números de Fibonacci não é constante.

Esta sequência não se repetiu o 1, pois em Quadrado Mágico não há números repetidos.

Números de Fibonacci

Número	Diferença

1
	1
2
	1
3
	2
5
	3
8
	5
13
	8
21
	13
34
	21
55

www.osfantasticosnumerosprimos.com.br

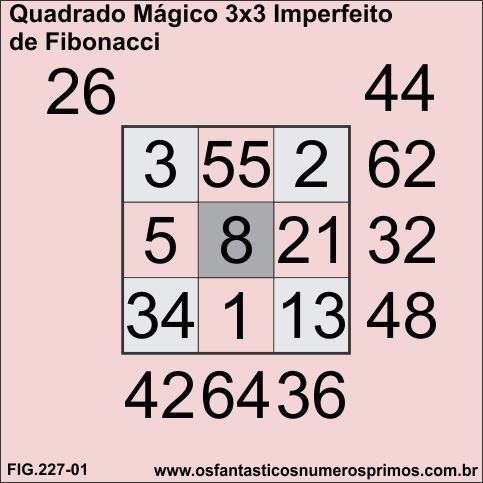
Não é possível formar Quadrado Mágico com os 9 termos da Sequência de Fibonacci, pois não há constante mágica.

A soma das linhas e a soma das colunas têm os mesmos resultados: 225.

Quadrado Mágico
Imperfeito 3x3
de Fibonacci
			44
5	55	2	62
3	8	21	32
34	1	13	48
42	64	36	26

Sequência dos 9 primeiros múltiplos de 2 dos números de Fibonacci

A diferença entre cada termo da sequência dos 9 primeiros múltiplos de 2 da Sequência de Fibonacci não é constante.

Números de Fibonacci

Múltiplos de 2

Número	Diferença

2
	6
8
	26
34
	110
144
	466
610
	1974
2584
	8362
10946
	35422
46368
	150050
196418

www.osfantasticosnumerosprimos.com.br

Não é possível formar Quadrado Mágico com os 9 primeiros múltiplos de 2 da Sequência de Fibonacci, pois não há constante mágica.

A soma das linhas e a soma das colunas têm os mesmos resultados: 257.114.

Quadrado Mágico
Imperfeito 3x3
Fibonacci
			46986
144	196418	8	196570
34	610	10946	11590
46368	2	2584	48954
46546	197030	13538	3338

Sequência dos 9 primeiros múltiplos de 3 dos números de Fibonacci

A diferença entre cada termo da sequência dos 9 primeiros múltiplos de 3 da Sequência de Fibonacci não é constante.

Números de Fibonacci

Múltiplos de 3

Número	Diferença

3
	18
21
	123
144
	843
987
	5778
6.765
	39.603
46.368
	271.443
317.811
	1.860.498
2.178.309
	12.752.043
14.930.352

www.osfantasticosnumerosprimos.com.br

Não é possível formar Quadrado Mágico com os 9 primeiros múltiplos de 3 da Sequência de Fibonacci, pois não há constante mágica.

A soma das linhas e a soma das colunas têm os mesmos resultados: 17.480.760.

Quadrado Mágico
Imperfeito 3x3
Fibonacci
			2185095
987	14930352	21	14931360
144	6765	317811	324720
2178309	3	46368	2224680
2179440	14937120	364200	54120

Quadrado Mágico Multiplicativo Imperfeito 3x3 - Fibonacci

Quadrado Mágico Multiplicativo é o quadrado em que os termos de cada linha, cada coluna e diagonais são multiplicados.

Não é possível formar Quadrado Mágico Múliplicativo Perfeito com os 9 primeiros números da Sequência de Fibonacci, pois não há constante mágica.

A soma das linhas e a soma das colunas têm os mesmos resultados: 1.496.

Quadrado Mágico
Imperfeito 3x3
9 números de Fibonacci
			544


5	55	2	550
3	8	21	504
34	1	13	442

510	440	546	520

Não é possível formar Quadrado Mágico Múliplicativo Perfeito com os 9 primeiros múltiplos de 2 da Sequência de Fibonacci, pois não há constante mágica.

A soma das linhas e a soma das colunas têm os mesmos resultados: 692.923.400.

Quadrado Mágico
Imperfeito 3x3
múltiplos de 2

			226.275.840


144	196418	8	226.273.536
34	610	10946	227.020.040
46368	2	2584	239.629.824

227.017.728	239.629.960	226.275.712	226.978.560

Não é possível formar Quadrado Mágico Múliplicativo Perfeito com os 9 primeiros múltiplos de 3 da Sequência de Fibonacci, pois não há constante mágica.




Quadrado Mágico
Imperfeito 3x3
múltiplos de 3

987	14930352	21
144	6765	317811
2178309	3	46368

produto da primeira linha = 309.461.405.904

produto da segunda linha = 309.598.763.760

produto da terceira linha = 303.011.495.136

produto da primeira coluna = 309.598.701.552

produto da segunda coluna = 303.011.493.840

produto da terceira coluna = 309.461.469.408

A soma das linhas e a soma das colunas têm os mesmos resultados: 922.071.664.800.

Conclusão:

Será que Quadrado Mágico é o Calcanhar de Aquiles na Sequência de Fibonacci?

Será que existe ao menos uma sub-sequência de Fibonacci em que é possível construir Quadrado Mágico?

A Sequência de Fibonacci possui diversas propriedades numéricas mas com alguns Quadrados Mágicos elementares não houve êxito.

Can a 3x3 magic square be constructed with nine distinct square numbers? This short question asked by Martin LaBar in 1984 became famous when Martin Gardner republished it in 1996 and offered $100 to the first person to construct such a square. Two years later, Gardner wrote:

So far no one has come forward with a “square of squares” – but no one has proved its impossibility either. If it exists, its numbers would be huge, perhaps beyond the reach of today’s fastest computers.

Fonte: http://www.multimagie.com

Pode um quadrado mágico de 3x3 ser construído com nove números quadrados distintos? Esta pequena pergunta feita por Martin LaBar em 1984 tornou-se famosa quando Martin Gardner a republicou em 1996 e ofereceu US$ 100 para a primeira pessoa a construir tal quadrado. Dois anos depois, Gardner escreveu:

Até agora ninguém avançou com um “quadrado de quadrados” - mas ninguém provou sua impossibilidade. Se existir, seus números seriam enormes, talvez além do alcance dos computadores mais rápidos de hoje.

Parafraseando Martin Labar, será que é possível construir Quadrado Mágico Fibonático, isto é, com números da Sequência de Fibonacci?

Autor: Ricardo Silva - julho/2019