


Quadrados Mágicos Multiplicativos são quadrados em que os números de cada linha, cada coluna e diagonais são multiplicados e os produtos de cada um deles formam Constante Mágica.
Quantos Quadrados Mágicos Multiplicativos de ordem ímpar 3x3 formados por sequências numéricas de 9 divisores podem ser construídos?
Consultando a Tabela de Divisores - Wikipédia - a enciclopédia livre que listam todos os divisores dos números de 1 a 1000, verifica-se que determinados números quadrados perfeitos também possuem divisores em quantidade de números quadrados perfeitos, haja vista, que podemos formar infinitas progressões aritméticas de números consecutivos, números pares, números ímpares, etc...
A tabela apresenta regularidades nas formações de divisores de números quadrados perfeitos:
a) coluna Número - são números quadrados perfeitos;
b) coluna Divisores - o termo médio é uma raiz quadrada;
c) coluna Quantidade - as sequências possuem 9 termos.
d) a diferença entre dois termos, isto é a razão, de cada sequência não é constante;
e) o produto de termos equidistantes de cada sequência tem como resultado número quadrado perfeito;
f) o termo médio ao quadrado é igual ao último termo da sequência;
g) a média geométrica de dois termos equidistantes tem como resultado a raiz quadrada do útimo termo da sequência.
| Tabelas de Divisores de | |||
|---|---|---|---|
| Números Quadrados Perfeitos | |||
| Raiz | Número | Divisores | Quantidade |
| 6 | 36 | 1, 2, 3, 4, 6, 9, 12, 18, 36 | 9 |
| 10 | 100 | 1, 2, 4, 5, 10, 20, 25, 50, 100 | 9 |
| 14 | 196 | 1, 2, 4, 7, 14, 28, 49, 98, 196 | 9 |
| 15 | 225 | 1, 3, 5, 9, 15, 25, 45, 75, 225 | 9 |
| 16 | 256 | 1, 2, 4, 8, 16, 32, 64, 128, 256 | 9 |
| 21 | 441 | 1, 3, 7, 9, 21, 49, 63, 147, 441 | 9 |
| 22 | 484 | 1, 2, 4, 11, 22, 44, 121, 242, 484 | 9 |
| 26 | 676 | 1, 2, 4, 13, 26, 52, 169, 338, 676 | 9 |
Fonte: Tabela adaptada de
[2] https://pt.wikipedia.org
A razão entre os divisores do número 36 não é constante, isto é, há quantidades diferentes de razões, portanto não formam progressão aritmética (P.A.) e nem progressão geométrica (P.G.).
| Divisores do número | |
|---|---|
| quadrado perfeito 36 | |
| Divisores | Diferença |
| 1 | |
| 1 | |
| 2 | |
| 1 | |
| 3 | |
| 1 | |
| 4 | |
| 2 | |
| 6 | |
| 3 | |
| 9 | |
| 3 | |
| 12 | |
| 6 | |
| 18 | |
| 18 | |
| 36 | |
| www.osfantasticosnumerosprimos.com.br | |
Construindo um quadrado conforme a configuração do Quadrado Mágico Lo-Shu e escolhendo-se um dos métodos de construções como: Cruz e "Xis" e Yang Hui com a sequência dos divisores do número 36, obtem-se um Quadrado Mágico Multiplicativo Imperfeito, pois os produtos das linhas, das colunas e diagonais não formam Constante Mágica em sua totalidade.
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| Imperfeito | ||||
| 216 | ||||
| 4 | 36 | 2 | = | 288 |
| 3 | 6 | 12 | = | 216 |
| 18 | 1 | 9 | = | 162 |
| = | = | = | ||
| 216 | 216 | 216 | 216 | |
Construindo-se um quadrado com a permutação dos pares de números equidistantes:
3 e 12 na diagonal principal,
4 e 9 na linha horizontal central,
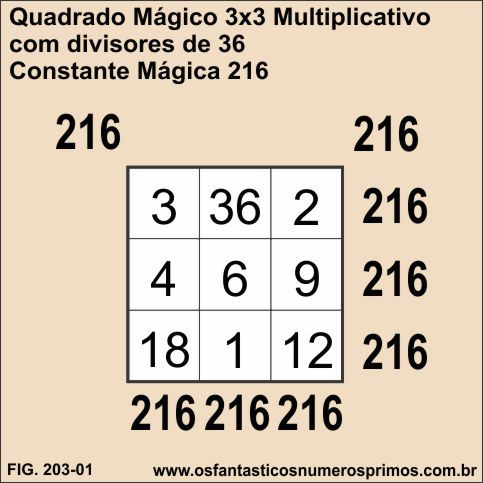
obtem-se um Quadrado Mágico Multiplicativo, pois os produtos das linhas, das colunas e diagonais formam Constante Mágica em sua totalidade.
Como se percebe é uma construção de Quadrado Mágico que não segue as regras de métodos tradicionais para construção de Quadrados Mágicos como: Cruz e "Xis" e Yang Hui.
Constante Mágica 216
Soma dos termos 91
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| constante mágica 216 | ||||
| 216 | ||||
| 3 | 36 | 2 | = | 216 |
| 4 | 6 | 9 | = | 216 |
| 18 | 1 | 12 | = | 216 |
| = | = | = | ||
| 216 | 216 | 216 | 216 | |
Fonte: [1] Marques, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
Elevando-se os termos do Quadrado Multiplicativo ao quadrado e somando as linhas, colunas e diagonais obtem-se um Quadrado Mágico Imperfeito.
Soma dos termos 1.911
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| ao quadrado - imperfeito | ||||
| 364 | ||||
| 9 | 1296 | 4 | = | 1309 |
| 16 | 36 | 81 | = | 133 |
| 324 | 1 | 144 | = | 469 |
| = | = | = | ||
| 349 | 1333 | 229 | 189 | |
Multiplicando-se os termos elevados ao quadrado das linhas, colunas e diagonais, obtem-se Quadrado Mágico Multiplicativo.
Constante Mágica 46.656
Soma dos termos 1.911
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| ao quadrado | ||||
| 46.656 | ||||
| 9 | 1296 | 4 | = | 46.656 |
| 16 | 36 | 81 | = | 46.656 |
| 324 | 1 | 144 | = | 46.656 |
| = | = | = | ||
| 46.656 | 46.656 | 46.656 | 46.656 | |
Elevando-se os termos do Quadrado Multiplicativo ao cubo e somando as linhas, colunas e diagonais obtem-se um Quadrado Mágico Imperfeito.
Soma dos termos 55.261
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| ao cubo - imperfeito | ||||
| 6056 | ||||
| 27 | 46656 | 8 | = | 46691 |
| 64 | 216 | 729 | = | 1009 |
| 5832 | 1 | 1728 | = | 7561 |
| = | = | = | ||
| 5923 | 46873 | 2465 | 1971 | |
Multiplicando-se os cubos das linhas, colunas e diagonais, obtem-se Quadrado Mágico Multiplicativo.
Constante Mágica 10.077.696
Soma dos termos 55.261
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| ao cubo | ||||
| 10077696 | ||||
| 27 | 46656 | 8 | = | 10077696 |
| 64 | 216 | 729 | = | 10077696 |
| 5832 | 1 | 1728 | = | 10077696 |
| = | = | = | ||
| 10077696 | 10077696 | 10077696 | 10077696 | |
Elevando-se os termos do Quadrado Multiplicativo à quarta potência e somando as linhas, colunas e diagonais obtem-se um Quadrado Mágico Imperfeito.
Soma dos termos 1.813.539
| Quadrado Mágico | ||||
| Multiplicativo 3x3 | ||||
| à 4a potência - imperfeito | ||||
| 106288 | ||||
| 81 | 1679616 | 16 | = | 1679713 |
| 256 | 1296 | 6561 | = | 8113 |
| 104976 | 1 | 20736 | = | 125713 |
| = | = | = | ||
| 105313 | 1680913 | 27313 | 22113 | |
Multiplicando-se às quartas potências das linhas, colunas e diagonais, obtem-se Quadrado Mágico Multiplicativo.
Constante Mágica 2.176.782.336
Soma dos termos 1.813.539
| Quadrado Mágico | ||
| Multiplicativo 3x3 | ||
| à 4a potência | ||
| 81 | 1679616 | 16 |
| 256 | 1296 | 6561 |
| 104976 | 1 | 20736 |
| = | = | = |
| 2176782336 | 2176782336 | 2176782336 |
soma de cada linha: 2176782336
soma de cada coluna : 2176782336
soma de cada diagonal : 2176782336
Divisores cujas sequências são de 9 termos, conforme tabela acima, as execeções, até o momento, são os divisores do número 36, 225 e 441 que para formarem Quadrado Mágico Multiplicativo foram necessários permutar dois grupos de termos equidistantes na construção de quadrado mágico.
Os demais divisores de: 100, 196, 256, e 484 não precisaram ser permutados para se construirem Quadrados Mágicos Multiplicativos.
Há de se observar que são 7 exemplos de sequências de divisores analisadas, 2 demonstradas aqui no WebSite num rol de 1000 números.
Outra constatação muito importante é que elevando-se os termos de um Quadrado Mágico Multiplicativo ao quadrado, ao cubo, à quarta potência e posteriormente multiplicando-se linhas, colunas e diagonais, obtêm-se Quadrados Multi-Mágicos Multiplicativos de quadrado, de cubo e de quarta potência, conforme exemplos demonstrados.
Quadrado Mágico 3x3 Normal, formado com a sequência numérica de 1 a 9 e elevando-se cada termo ao quadrado, ao cubo e à quarta potência e posteriormente multiplicando-se linhas, colunas e diagonais não formaram Quadrados Multi-Mágicos Multiplicativos.
Autor: Ricardo Silva - setembro/2018
[1] MARQUES, Jamerson Henriques da Silva. Estudo do quadrado mágico com uso nos anos finais do ensino fundamental / Jamerson Henrique da Silva Marques. – 2017. 96 p. Dissertação (mestrado) – Universidade Federal do Rio Grande – FURG, Programa de Pós-graduação em Matemática, Rio Grande/RS, 2017.
[2] https://pt.www.wikipedia.org
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato