


Quadrados Mágicos 3x3 ou de ordem 3 são matrizes quadriculadas formadas por linhas e colunas nas quais podem ser dispostas sequências numéricas em certa ordem de forma que a soma de cada linha, cada coluna e cada diagonal tenham um mesmo resultado o qual é denominado de Constante Mágica.
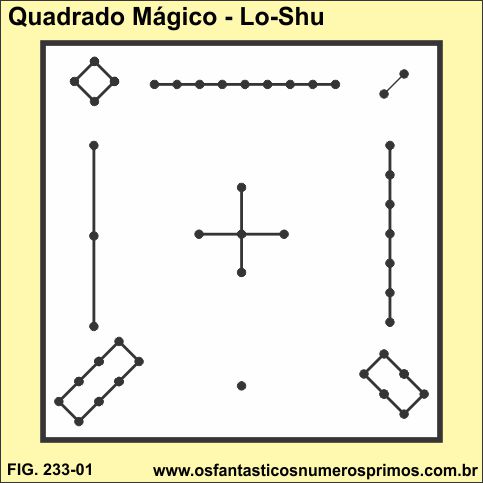
Segundo lendas e estórias chinesas, um Quadrado Mágico apareceu no casco de uma tartagura e que posteriormente foi chamado de Lo-Shu.
Quadrados Gregos-Latinos, ou simplesmente Quadrados Latinos são matrizes nas quais podem ser utilizados símbolos, como numerais, letras de alfabetos e outros símbolos de forma que cada célula contenha um único símbolo e que não haja repetição em linhas ou colunas.
O nome Quadrado Grego-Latino tornou-se popular devido aos estudos do Matemático Leonhard Euler (1707-1783) em tentar solucionar o seguinte problema:
"É possível alinhar 36 oficiais em uma formação de seis linhas por seis colunas, de modo que cada linha e cada coluna tenha apenas um oficial de cada posto e de cada regimento?"
A partir de Quadrados Mágicos, Euler trabalhou com quadrados latinos ortogonais na tentativa de solucionar tal problema, conjecturando que não havia solução.
O uso de letras não foi uma exclusividade nos trabalhos de Euler, pois haviam amuletos arábes e indianos com inscrições com letras em Quadrados Mágicos e no livro “O sol do grande conhecimento” de Ahmed Al-Buni - escrito por volta do ano 1200 - há registros de construções de quadrados latinos ortogonais que ficou conhecido como Método Hindu.[1]
Um Quadrado Latino Reduzido é uma matriz quadrada de ordem n × n , onde suas entradas são os números do conjunto {1,2,...,n}, ou qualquer conjunto que tenha uma sequência primitiva, onde apresentam, ambas, primeira linha e primeira coluna os elementos em sua ordem primitiva. [2]
Quadrado 1
sequência 1, 2, 3
| Quadrado Latino Reduzido | ||
| 1 | 2 | 3 |
| 2 | 3 | 1 |
| 3 | 1 | 2 |
Quadrado 2
sequência a, b, c (alfabeto latino)
| Quadrado Latino Reduzido | ||
| a | b | c |
| b | c | a |
| c | a | b |
Quadrado 3
sequência α, β, γ (alfabeto grego)
| Quadrado Latino Reduzido | ||
| α | β | γ |
| β | γ | α |
| γ | α | β |
Combinando-se os termos correspondentes dos quadrados latinos reduzidos:
Quadrado 2
| Quadrado Latino Reduzido | ||
| a | b | c |
| b | d | a |
| d | a | b |
com o Quadrado 3
| Quadrado Latino Reduzido | ||
| α | β | γ |
| β | γ | α |
| γ | α | β |
não é possível formar Quadrado Latino Ortogonal, pois ocorrem repetição de pares ordenados: (aα, aα), (bβ, bβ), (cγ, cγ).
| aα | bβ | cγ |
| bβ | bγ | aα |
| cγ | aα | bβ |
Quadrado Latino Ortogonal é a combinação de dois outros quadrados latinos que formam pares ordenados distintos, isto é, que não se repetem em linhas ou colunas.
Combinando-se os quadrados reduzidos:
Quadrado 2
| Quadrado Latino | ||
| a | b | c |
| b | c | a |
| c | a | b |
com o Quadrado 3, de forma que o termo "γ" fique em diagonal oposta ao quadrado 2...
| Quadrado Latino | ||
| γ | β | α |
| α | γ | β |
| β | α | γ |
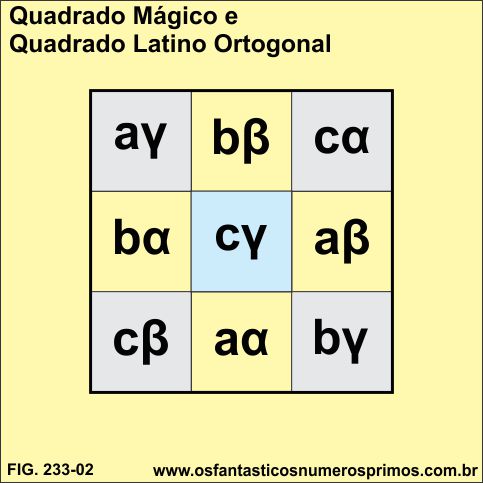
...é possível formar Quadrado Latino Ortogonal, pois os pares ordenados são distintos.
| Quadrado Latino Ortogonal | ||
| aγ | bβ | cα |
| bα | cγ | aβ |
| cβ | aα | bγ |
As sequências devem obedecer as seguintes regras:
a) Quadrado-2 e Quadrado-3 deve gerar 9 pares ordenados distintos;
b) a sequência das letras latinas devem obedecer uma progressão aritmética de razão 3, resultando no tamanho da matriz;
c) a + b = 2c;
d) a sequências das letras gregas devem obedecer uma progressão geométrica de razão 1.
e) na diagonal principal de Quadrado-2, temos (a, c, b);
f) na diagonal secundária de Quadrado-3, temos (α, γ, β).
Sejam as sequências:
(a, c, b) = (1, 4, 7)
(α, γ, β) = (3, 4, 5)
e seus respectivos quadrados latinos:
Quadrado 2
| Quadrado Latino | ||
| 1 | 7 | 4 |
| 7 | 4 | 1 |
| 4 | 1 | 7 |
Quadrado 3
| Quadrado Latino | ||
| 4 | 5 | 3 |
| 3 | 4 | 5 |
| 5 | 3 | 4 |
Somando-se os os números das células correspondentes...
| 1 + 4 | 7 + 5 | 4 + 3 |
| 7 + 3 | 4 + 4 | 5 + 1 |
| 4 + 5 | 1 + 3 | 7 + 4 |
...obtem-se o seguinte Quadrado Mágico de Constante Mágica 24.
| Quadrado Mágico | ||
| 5 | 12 | 7 |
| 10 | 8 | 6 |
| 9 | 4 | 11 |
Subtraindo-se 3 (ordem do Quadrado Mágico)...
| 5 - 3 | 12 - 3 | 7 - 3 |
| 10 - 3 | 8 - 3 | 6 - 3 |
| 9 - 3 | 4 - 3 | 11 - 3 |
...obtem-se uma variante do Quadrado Mágico Lo-Shu.
| Variante do | ||
| Quadrado Mágico Lo-shu | ||
| 2 | 9 | 4 |
| 7 | 5 | 3 |
| 6 | 1 | 8 |
No método de Philipe de La Hire, os termos centrais das sequências também ficam em diagonais opostas. [3]
sejam as sequências:
(1, 2, 3) - quantidade linhas/colunas do quadrado,
(0, 3, 6) - múltiplos de 3
e seus respectivos quadrados latinos
Quadrado 1
| Quadrado Latino | ||
| 3 | 0 | 6 |
| 6 | 3 | 0 |
| 0 | 6 | 3 |
Quadrado 2
Observação: a sequência 1, 2, 3 forma uma "cruz".
| Quadrado Latino | ||
| 3 | 1 | 2 |
| 1 | 2 | 3 |
| 2 | 3 | 1 |
Somando-se os os números das células correspondentes...
| 3 + 3 | 0 + 1 | 6 + 2 |
| 6 + 1 | 3 + 2 | 0 + 3 |
| 0 + 2 | 6 + 3 | 3 + 1 |
...obtem-se uma variante Quadrado Mágico Lo-Shu.
| Variante do | ||
| Quadrado Mágico Lo-shu | ||
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
Monta-se um quadrado latino de ordem 3, com sequência 1, 2, 3. [1]
Neste método, o termo central 2, também fica na diagonal.
Observação: a sequência 1, 2, 3 forma uma "cruz".
Quadrado 1
| Quadrado Latino | ||
| 3 | 1 | 2 |
| 1 | 2 | 3 |
| 2 | 3 | 1 |
Multiplica-se os termos da matriz pela ordem do quadrado, neste exemplo 3, obtendo-se o Quadrado-2.
Quadrado 2
| Quadrado Latino | ||
| 9 | 3 | 6 |
| 3 | 6 | 9 |
| 6 | 9 | 3 |
Soma-se os termos da coluna 1 (quadrado-1) com os termos da coluna 3 (quadrado-2);
Soma-se os termos da coluna 2 (quadrado-1) com os termos da coluna 2 (quadrado-2);
Soma-se os termos da coluna 3 (quadrado-1) com os termos da coluna 1 (quadrado-2).
| 3 + 6 | 1 + 3 | 2 + 9 |
| 1 + 9 | 2 + 6 | 3 + 3 |
| 2 + 3 | 3 + 9 | 1 + 6 |
obtendo-se o Quadrado Mágico de Costante Mágica 24.
| Quadrado Mágico 3x3 | ||
| Constante Mágica 24 | ||
| 9 | 4 | 11 |
| 10 | 8 | 6 |
| 5 | 12 | 7 |
Subtraindo-se 3 (ordem do Quadrado Mágico)...
| 9 - 3 | 4 - 3 | 11 - 3 |
| 10 - 3 | 8 - 3 | 6 - 3 |
| 5 - 3 | 12 - 3 | 7 - 3 |
...obtem-se uma variante do Quadrado Mágico Lo-Shu.
| Variante do | ||
| Quadrado Mágico Lo-shu | ||
| 6 | 1 | 8 |
| 7 | 5 | 3 |
| 2 | 9 | 4 |
Interessante observar que cada método tem suas particularidades mesmo utilizando diagonais como base de construção e ao mesmo tempo similaridades entre as matrizes em relação as disposições dos números ora formando uma "cruz" normal ora formando uma "cruz inversa" na linha e coluna central dos quadrados, detalhes estes que serviram de base a outros métodos para se contruírem Quadrados Mágicos de ordem superiores.
Autor: Ricardo Silva - outubro/2019
[1] SANTOS, Cristiane Aparecida dos. QUADRADOS LATINOS: Um estudo histórico-filosófico da matemática. Trabalho de Conclusão de Curso - Universidade Federal de Santa Catarina, Departamento de Matemática, Centro de Blumenau, 2018. 76 p.
[2] FARIAS, Fausto Gustavo. Quadrados Latinos e Quadrados Mágicos - Uma proposta didática. Dissertação de Mestrado. Universidade Federal da Paraíba Centro de Ciências Exatas e da Natureza Departamento de Matemática, 2017.
[3] ROUSE BALL, WW. Mathematical Recreation and Essays. Nova York, edição digital, 1905 - Gutenberg Project, 2008
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato