


Quadrados Mágicos são dispositivos numéricos, formados por células em quantidades de números quadrados perfeitos, nos quais dispondo sequências numéricas formadas por progressões aritméticas, progressões geométricas ou não em certa ordem, as somas de cada uma das linhas, cada uma das colunas, bem como, as diagonais tem como resultado um mesmo total, isto é, uma constante, denominada de Constante Mágica.
As demonstrações aqui apresentadas tem como base a obra: Pitágoras Africano: Um estudo em cultura e educação matemática, edição de 2011, de Paulus Pierre Joseph Gerdes (1952-2014), matemático, físico, antropólogo holandês. Tornou-se cidadão moçambicano em 1976, trabalhou na Universidade Pedagógica e fundou na cidade de Maputo o Centro de Pesquisas em Etnomatemática - Cultura, Matemática e Educação.
No decorrer das demonstrações, ver-se-á que os estudos do Professor Paulus Gerdes em relação a Quadrados Mágicos apresenta método de construção totalmente original, tendo como base, um artefato artesanal (esteira Cokwe) construído por comunidades do nordeste de Angola, país situado no continente africano.
Na montagem da Esteira Cokwe, cada tira escura passa por cima de uma tira clara e depois debaixo de quatro tiras claras.

Delimitando-se o entrelaçamento na Esteira Cokwe em uma matriz de 5x5 (25 células) e posteriormente númerando-as onde as tiras escuras se destacam, observa-se que cada parte da tira escura aparece em cada linha e em cada coluna, somente um vez, isto é, partes das tiras não se repetem, formando-se assim um padrão de entrelaçamento.
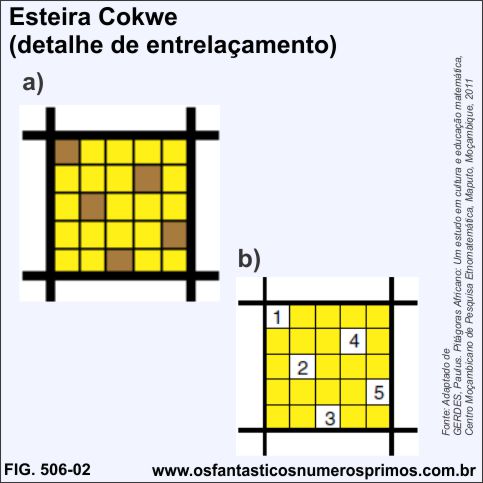
Observação importantíssima:
no detalhe b), a partir do número 1, desce-se 2 células, vire à direita e marca-se o número 2;
a partir do número 2, desce-se 2 células, vire à direita e marca-se o número 3;
a partir do número 3, conta-se 2 células a partir do topo, vire à direita e marca-se o número 4;
e por fim, a partir do número 4, desce-se 2 células, vire à direita e marca-se o número 5.
Na matriz 5x5 a), tem-se a ordem com que as tiras escuras se destacam na própria matriz e abaixo, linhas guias para melhor observar as direções e posições dos números.
Executando rotações, exemplos b), d) e e), os números aparecem em outras posições na matriz 5x5.
A única matriz 5x5 diferente é matriz c), na qual o número 5 aparece na célula central, e os números 1, 2, 3, 4 formando vértices de um quadrado.
Sobrepondo-se as matrizes uma em cima da outra, obtem-se um quadrado latino, delhate f).
Quadrado Latino é uma matriz que pode ser construída por números, letras ou outros tipos de símbolos de forma que em cada linha e em cada coluna ocorra uma só vez e não podendo haver repetição dos mesmos.
Exemplo clássico originado de Quadrado Latino é o popular passatempo Sudoku em que se tem que escrever números de 1 a 9 em uma matriz quadriculada formada por 9 quadrados de 3x3 células sem que haja repetição desses mesmos números em linhas e colunas.
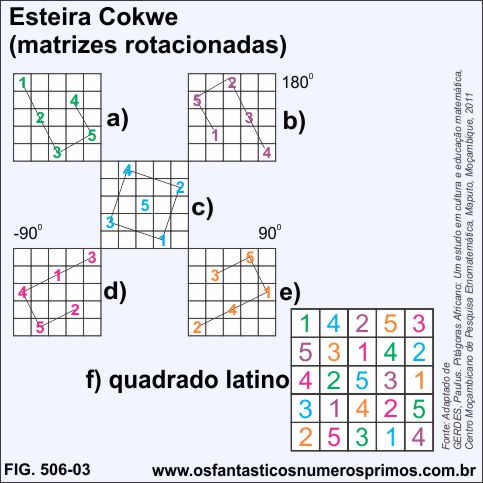
Na matriz b), somando-se 5 unidades a cada número; na matriz c), somando-se 15 unidades a cada número; na matriz d), somando-se 10 unidades a cada número e por fim, somando-se 20 unidades a cada número da matriz e), obtem-se um quadrado mágico 5x5.
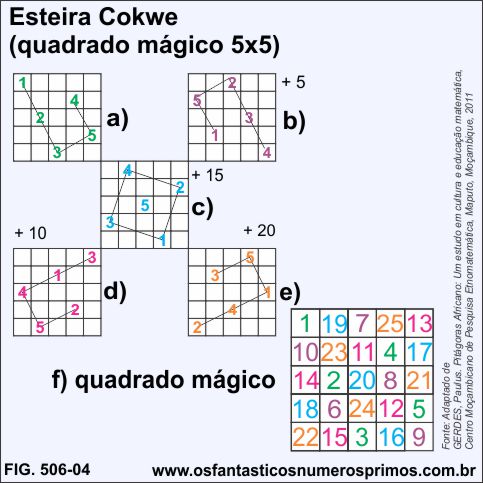
A construção do quadrado latino 5x5 de Paulus Gerdes, pode ser mais dinâmico, isto é, mais simplicado, vejamos:
a) coloca-se o número 1 (cor verde) na primeira célula da matriz 5x5;
b) desce-se 2 células verticalmente e anda-se 1 célula em sentido horizontal à direita e coloca-se o número 2 (cor verde);
c) o número 3 se encontra na última linha da matriz, conta-se duas células verticalmente, começando-se a partir da primeira linha da matriz, na mesma coluna do 3, deslocando-se à direita, coloca-se o número 4 (cor verde);
d) a partir do 5 é um caso especial, é a própria ordem da matriz 5x5, é quantidade de células dos lados da matriz;
e) 5 (cor verde) se encontra na última coluna, desloca-se 2 células em sentido horizontal, a partir da primeira célula da mesma linha em que se encontra o 5 e coloca-se o número 1 (cor lilás);
f) seguindo-se estes de deslocamentos e marcações de números, constrói-se assim um quadrado latino 5x5.
Interessante observar que:
g) as alocações dos números 1 a 4 são movimentos em formato da letra L (éle), semelhante ao movimento da peça do Cavalo do Jogo de Xadrez;
h) as alocações de números a partir do 5 (ordem da matriz), os movimentos se dão em sentido horizontal, semelhantes aos movimentos das peças da Dama (Rainha) ou da Torre do Jogo de Xadrez.

Uma outra característa na estrutura do Quadrado Latino de Paulus Gerdes é que o número 5 (ordem da matriz 5x5) se encontra na célula central, e os números de 1 a 5 podem ser escritos ou lidos, sempre começando pelo próprio 5, vejamos:
a) coluna central: 5, 4 3, sobe, 2 e 1;
b) quarta coluna: 5, 4, 3, 2 e 1;
c) terceira coluna: 5, sobe, 4, 3, 2, e 1;
d) primeira coluna: 5, 4, 3 e 2, sobe, e 1;
e) quinta coluna: 5, 4, sobe e 3, 2, e 1;
Observações importantes:
f) as posições dos números 5's formam um quadrado dentro da matriz 5x5;
g) os números 5's estão alocados há 1 célula dos vértices da matriz e como veremos, a seguir, os múltiplos de 5: 5, 15, 10 e 25 também se encontram alocados nas células dos números 5's.
Características estas, se forem regulares, podem ser construídos outros quadrados latinos e quadrados mágicos de outras ordens ímpares, tornando-se um padrão de construção de quadrados mágicos, isto é, um novo método.
Seguindo-se as mesmas etapas de construção do Quadrado Latino 5x5 de Paulus Gerdes, constrói-se também quadrado mágico 5x5, as observações que se fazem são as seguintes:
a) o número 9 (cor lilás) se encontra na última célula, da última linha e coluna da matriz;
b) o número 10 (cor lilás) foi alocado a partir do canto superior esquedo, na célula da primeira coluna e segunda linha da matriz;
c) números consecutivos de múltiplos de 5 (ordem 5x5 do quadrado): 5, 10, 15, 20, devem ser alocados em sentido horizontal, obdecendo-se o deslocamento de 2 células a partir de um múltiplo de 5 (neste caso a ordem do quadrado).
Interessante observar que:
d) as alocações de números que não são múltiplos de 5, os movimentos são em formato da letra L (éle), semelhante ao movimento da peça do Cavalo do Jogo de Xadrez;
e) as alocações de números a partir de um múltiplo de 5 (ordem da matriz), os movimentos se dão em sentido horizontal, semelhantes aos movimentos das peças da Dama (Rainha) e da Torre do Jogo de Xadrez, deslocando-se 2 células.
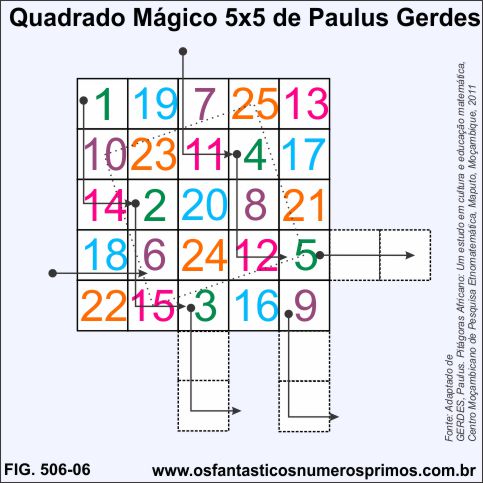
Analisando o Quadrado Mágico 5x5 de Paulus Gerdes, constata-se que:
a) nas diagonais, não há sequências de números consecutivos;
b) a soma de dois números equidistantes não somam o número central 20;
c) os múltiplos de 5: 5, 15, 10, 25 se encontram alinhados formando vértices de um quadrado e ao centro o múltiplo 20;
d) é um quadrado diabólico / pandiagonal, pois a soma de diagonais quebradas resultam na Constante Mágica 65;
7 + 23 + 14 + 5 + 16 = 65
7 + 4 + 21 + 18 + 15 = 65
1 + 17 + 8 + 24 + 15 = 65
e) as alocações de números a partir de múltiplos de 5 é o que difere o Método Paulus Gerdes do Método de Moschopulus 2, publicado no livro digital Magic Squares de Holger Danielsson - Version 2.12 (date: 05. Mar 2022) - capítulo 4.1.3 Moschopoulos 2, pag. 112.

No Quadrado Mágico 5x5 de Paulus Gerdes, o Terno Pitagórico 3-4-5, bem como, seus respectivos quadrados perfeitos 9-16-25 formam triangulações, isto é, são vértices de figuras de triângulos retângulos.

No Quadrado Mágico 5x5 de Paulus Gerdes, a primeira linha e a última coluna são formadas por números ímpares, com ocorrências números primos.

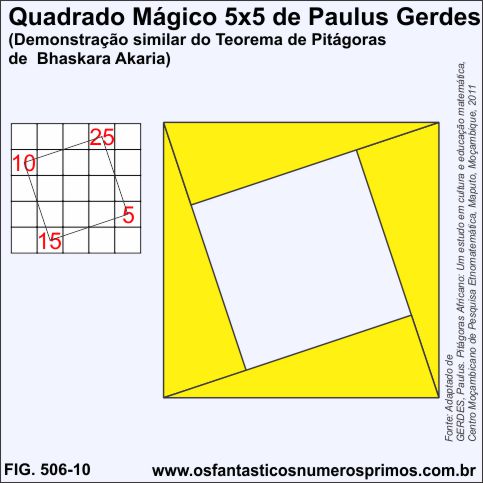
No Quadrado Mágico 5x5 de Paulus Gerdes, prolongando os lados do quadrado inscrito cujos vértices são múltiplos de 5, obtem-se uma demonstração similar do Teorema de Pitágoras por Bhaskara Akaria.
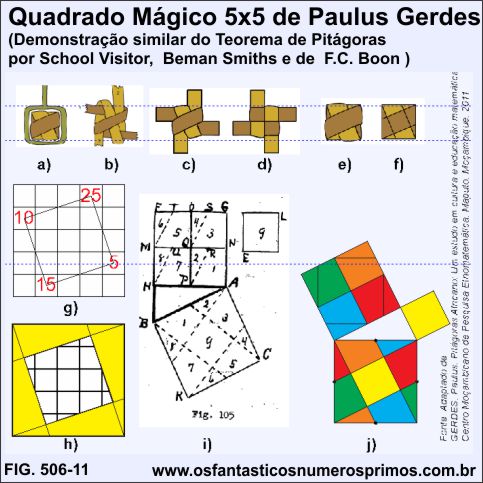
Estudos realizados pelo Professor Paulus Gerdes em entrelaçamento de um botão quadrado por 2 pedaços de fitas coloridas demonstram que a forma final do entrelaçamento tem como base o Teorema de Pitágoras.
As figuras dos detalhes de a) a f) demonstram as etapas do estudo do entrelaçamento e padrões geométricos.
No Quadrado Mágico 5x5 de Paulus Gerdes, prolongando-se os lados do quadrado inscrito cujos vértices são múltiplos de 5, obtem-se padrão geométrico h) semelhante a figura f), um quadrado, 4 triângulos e 4 trapézios
Consultando a obra The Pythagorean Propositions de Elisha Scott Loomis, edição digital de 1968, página 100, exemplo 2, se encontra a demonstração geométrica do Teorema de Pitágoras i), creditadas à Revista School Visitor de 1882, volume III, a Beman and Smiths Row´s - 1905 e a F.C. Boon.
Esta demonstração do Teorema de Pitágoras podem ser construídas das seguintes formas:
a) com 4 quadrados, traçando-se um segmento a partir do ponto médio de um dos lados até um dos vértices, desta forma se têm 4 triângulos e 4 trapézios;
b) ou a partir de um só quadrado, a partir de cada ponto médio de cada lado, traçar seguimentos até os vértices, desta forma se obtêm: 4 triângulos, 4 trapézios e um quadrado menor.
Interessante observar que esta demonstração i) do Teorema de Pitágoras também se assemelha a de Henry Perigal por decomposição de figuras geométricas.
O Quadrado Mágico 7x7 de Paulus Gerdes apresenta as seguintes propriedades:
a) a primeira linha e a última coluna são formadas por números ímpares, entre eles, número primos;
b) os múltiplos de 7 aparecem em diagonais quebradas;
c) o Terno Pitagórico 7-24-25 formam triangulação.
d) nas diagonais principal e secundária não são formadas por números consecutivos.
| Quadrado Mágico 7x7 | |||||||
| Paulus Gerdes | |||||||
| 175 | |||||||
| 1 | 33 | 9 | 41 | 17 | 49 | 25 | 175 |
| 38 | 21 | 46 | 22 | 5 | 30 | 13 | 175 |
| 26 | 2 | 34 | 10 | 42 | 18 | 43 | 175 |
| 14 | 39 | 15 | 47 | 23 | 6 | 31 | 175 |
| 44 | 27 | 3 | 35 | 11 | 36 | 19 | 175 |
| 32 | 8 | 40 | 16 | 48 | 24 | 7 | 175 |
| 20 | 45 | 28 | 4 | 29 | 12 | 37 | 175 |
| 175 | 175 | 175 | 175 | 175 | 175 | 175 | 175 |
O Quadrado Semi Mágico 9x9 de Paulus Gerdes apresenta as seguintes propriedades:
a) a primeira linha e a última coluna são formadas por números ímpares, entre eles, número primos;
b) os múltiplos de 9 aparecem em diagonais quebradas;
c) o Terno Pitagórico 9-40-41 formam triangulação;
d) nas diagonais principal e secundária não são formadas por números consecutivos;
e) a soma da diagonal principal não apresenta a Constante Mágica 369, pois há uma diferença de 9 unidades.
| Quadrado Semi Mágico 9x9 | |||||||||
| Paulus Gerdes | |||||||||
| 369 | |||||||||
| 1 | 51 | 11 | 61 | 21 | 71 | 31 | 81 | 41 | 369 |
| 26 | 67 | 36 | 77 | 37 | 6 | 47 | 16 | 57 | 369 |
| 42 | 2 | 52 | 12 | 62 | 22 | 72 | 32 | 73 | 369 |
| 58 | 27 | 68 | 28 | 78 | 38 | 7 | 48 | 17 | 369 |
| 74 | 43 | 3 | 53 | 13 | 63 | 23 | 64 | 33 | 369 |
| 18 | 59 | 19 | 69 | 29 | 79 | 39 | 8 | 49 | 369 |
| 34 | 75 | 44 | 4 | 54 | 14 | 55 | 24 | 65 | 369 |
| 50 | 10 | 60 | 20 | 70 | 30 | 80 | 40 | 9 | 369 |
| 66 | 35 | 76 | 45 | 5 | 46 | 15 | 56 | 25 | 369 |
| 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | 369 | 360 |
O Quadrado Mágico 11x11 de Paulus Gerdes apresenta as seguintes propriedades:
a) a primeira linha e a última coluna são formadas por números ímpares, entre eles, número primos;
b) os múltiplos de 11 aparecem em diagonais quebradas;
c) o Terno Pitagórico 11-60-61 formam triangulação;
d) nas diagonais principal e secundária não são formadas por números consecutivos.
| Quadrado Mágico 11x11 | |||||||||||
| Paulus Gerdes | |||||||||||
| 671 | |||||||||||
| 1 | 73 | 13 | 85 | 25 | 97 | 37 | 109 | 49 | 121 | 61 | 671 |
| 92 | 43 | 104 | 55 | 116 | 56 | 7 | 68 | 19 | 80 | 31 | 671 |
| 62 | 2 | 74 | 14 | 86 | 26 | 98 | 38 | 110 | 50 | 111 | 671 |
| 32 | 93 | 44 | 105 | 45 | 117 | 57 | 8 | 69 | 20 | 81 | 671 |
| 112 | 63 | 3 | 75 | 15 | 87 | 27 | 99 | 39 | 100 | 51 | 671 |
| 82 | 33 | 94 | 34 | 106 | 46 | 118 | 58 | 9 | 70 | 21 | 671 |
| 52 | 113 | 64 | 4 | 76 | 16 | 88 | 28 | 89 | 40 | 101 | 671 |
| 22 | 83 | 23 | 95 | 35 | 107 | 47 | 119 | 59 | 10 | 71 | 671 |
| 102 | 53 | 114 | 65 | 5 | 77 | 17 | 78 | 29 | 90 | 41 | 671 |
| 72 | 12 | 84 | 24 | 96 | 36 | 108 | 48 | 120 | 60 | 11 | 671 |
| 42 | 103 | 54 | 115 | 66 | 6 | 67 | 18 | 79 | 30 | 91 | 671 |
| 671 | 671 | 671 | 671 | 671 | 671 | 671 | 671 | 671 | 671 | 671 | 671 |
Autor: Ricardo Silva - julho/2024
DANIELSSON, Holger, Magic Squares, Version 2.12 (date: 05. Mar 2022)
GERDES, Paulus, Pitágoras Africano: Um estudo em cultura e educação matemática, edição digital, 2011.
LOOMIS, Elisha Scott. The Pythagorean Propositions - by The National Council of Teachers of Mathematics, Inc. - 1968
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato