


O Passeio do Cavalo, ou o Problema do Cavalo, ou ainda Knight’s Tour Problem é um problema matemático no qual a peça do Cavalo do Jogo de Xadrez deve percorrer todas as casas do tabuleiro exatamente 1 vez em movimentos consecutivos.
Se a peça do Cavalo começar e terminar na mesma casa, diz-se que o problema é fechado, se começar e terminar em uma casa diferente, diz-se que o problema é aberto.
Harold James Ruthven Murray, mais conhecido como H. J. R. Murray, (1868-1955) foi um educador britânico, inspetor de escolas e proeminente historiador de xadrez. Em seu livro, A History of Chess, apresenta análises de um manuscrito árabe, datado de 840 d.C, de autoria de Abu Zakariya Yahya ben Ibrahim al-Hakim, com o título: Nuzhat al-arbab al-'aqulfi'sh-shatranj al-manqul no qual aparece o desenho de uma matriz 8x8 com o Passeio do Cavalo.
Outra variante do Problema do Cavalo, baseado em Quadrados Mágicos, é o Passeio Mágico do Cavalo ou Magic Knight's Tour que consiste em cada movimento do cavalo, numerar sequencialmente as casas por onde ele passa e que posteriormente somando-se as linhas horizontais e verticais, bem comos a diagonais, o resultado tem que ser uma constante, denominada de Constante Mágica, assim como em um Quadrado Mágico.
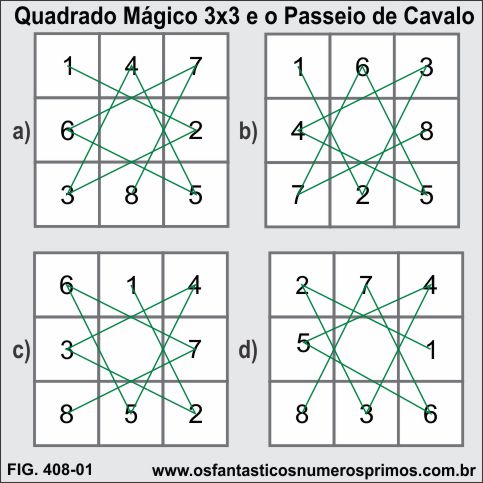
Na figura 408-01 abaixo, estão 4 exemplos demonstrando a impossibilidade de se construir um Quadrado Mágico 3x3 com movimentos da peça do Cavalo, pelo fato de se não conseguir alocar na célula central do quadrado o número 5 e também posicionar o número 9, pois as células se encontram ocupadas.
O movimento do Cavalo é duas casas a frente, ou para trás, ou para à direita ou para esquerda e virando-se uma casa a 90 graus, fazendo sempre o movimento em L (éle).
Interessante observar que duplas de números formados por ímpares e por pares se movimentam simetricamente.
Exemplos:
1 com 5
2 com 6
3 com 7
4 com 8
Assim como os quadrados 3x3, não possíveis de construirem Passeios Mágicos do Cavalo com quadrados quadriculados (n x n) ímpares.
Na figura 408-02 abaixo, estão 3 exemplos demonstrando Quadrados Mágicos 4x4 com peças do Jogo de Xadrez.
Segundo o Professor George Jelliss em WebSite:
https://www.mayhematics.com/t/1a.htm
são quadrados de números 2 e 619 que aparecem na lista de Bernad Frénicle de Bessy (1602-1675) e que o Professor George os reinterpretam como Passeios Mágicos da Rainha por apresentarem 3 e 4 movimentos diferentes.

Fonte: https://www.mayhematics.com/t/1a.htm
Por muito tempo, um problema matemático ficou em aberto, não se sabia se era possível ou não de se construir Quadrado Mágico 8x8 com o Passeio do Cavalo.
Em 2003, Jean-Charles Meyrignac, a partir de um software executado simultaneamente em rede com vários computadores e efetuando diversos cálculos matemáticos durante 61,40 dias, demonstrou que realmente não era possível se obter Quadrado Mágico 8x8 com o Passeio do Cavalo.
No WebSite:
http://magictour.free.fr
criado por Guenter Stertenbrink há diversos tópicos publicados com referências sobre Quadrados Mágicos e o Passeio do Cavalo.
Apesar de estarem nomeados como os primeiros Quadrados Mágicos 8x8 com Passeios do Cavalo, atribuídos a Willian Beverley, do ano de 1848, na verdade são Quadrados Semi-Mágicos 8x8 com Passeios do Cavalo.

Fonte: http://www.mayhematics.com/t/1d.htm
Os desenhos dos Quadrados Semi-Mágicos 8x8 (figura 408-03) estão publicados na obra A History of Chess de Harold James Ruthven Murray.
Reconstruíndo os quadrados com os Passeios do Cavalo em planilha digital, verifica-se que as diagonais não formam Constante Mágica. (células laranja)
| Quadrado Semi-Mágio 8x8 | ||||||||
| com Passeio do Cavalo | ||||||||
| de Willian Beverley (1848) | ||||||||
| 210 | ||||||||
| 1 | 30 | 47 | 52 | 5 | 28 | 43 | 54 | 260 |
| 48 | 51 | 2 | 29 | 44 | 53 | 6 | 27 | 260 |
| 31 | 46 | 49 | 4 | 25 | 8 | 55 | 42 | 260 |
| 50 | 3 | 32 | 45 | 56 | 41 | 26 | 7 | 260 |
| 33 | 62 | 15 | 20 | 9 | 24 | 39 | 58 | 260 |
| 16 | 19 | 34 | 61 | 40 | 57 | 10 | 23 | 260 |
| 63 | 14 | 17 | 36 | 21 | 12 | 59 | 38 | 260 |
| 18 | 35 | 64 | 13 | 60 | 37 | 22 | 11 | 260 |
| 260 | 260 | 260 | 260 | 260 | 260 | 260 | 260 | 282 |
| Quadrado Semi-Mágio 8x8 | ||||||||
| com Passeio do Cavalo | ||||||||
| de Willian Beverley (1848) | ||||||||
| 310 | ||||||||
| 64 | 35 | 18 | 13 | 60 | 37 | 22 | 11 | 260 |
| 17 | 14 | 63 | 36 | 21 | 12 | 59 | 38 | 260 |
| 34 | 19 | 16 | 61 | 40 | 57 | 10 | 23 | 260 |
| 15 | 62 | 33 | 20 | 9 | 24 | 39 | 58 | 260 |
| 32 | 3 | 50 | 45 | 56 | 41 | 26 | 7 | 260 |
| 49 | 46 | 31 | 4 | 25 | 8 | 55 | 42 | 260 |
| 2 | 51 | 48 | 29 | 44 | 53 | 6 | 27 | 260 |
| 47 | 30 | 1 | 52 | 5 | 28 | 43 | 54 | 260 |
| 260 | 260 | 260 | 260 | 260 | 260 | 260 | 260 | 238 |
Em 2003, Awani Kumar construiu um Quadrado Mágico 12x12 com o Passeio do Cavalo cuja Constante Mágica é 870 para todas as linhas e diagonais.

Independentemente dos quadrados serem mágicos ou não com o Passeio do Cavalo, os padrões geométricos que surgem com o movimento da peça do Cavalo são realmente padrões geométricos espetaculares.
O Professor George Jelliss em WebSite:
https://www.mayhematics.com/t/2a.htm
apresenta amplos estudos teóricos de Geometria relaciondas aos movimentos da peça do Cavalo em quadrados de várias ordens como: 3x3, 4x4, 5x5 e assim por diante com lindos padrões geométricos de encherem nossos olhos e nossas almas.
Autor: Ricardo Silva - dezembro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://www.mayhematics.com/t/1a.htm
http://www.mayhematics.com/t/1d.htm

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato