


O triângulo retângulo é uma figura geométrica realmente fantástica, uma figura geométrica totalmente assimétrica, pois seus lados apresentam comprimentos um maior que o outro e mesmo tendo essa "anomalia geométrica" possui diversas propriedades aritméticas, algébricas, trigonométricas, geométricas e numéricas os quais são utilizados para se fazerem os mais diversos cálculos nos diversos ramos das Ciências.
E quando a gente menos menos espera, lá está ele, o triângulo retângulo pitagórico aparecendo em lugares totalmente inusitados.
O Passeio do Cavalo, ou o Problema do Cavalo, ou ainda Knight’s Tour Problem é um problema matemático na qual a peça do Cavalo deve percorrer todas as casas do tabuleiro de Xadrez exatamente 1 vez em movimentos consecutivos.
Se a peça do Cavalo começar e terminar na mesma casa, diz-se que o problema é fechado, se começar e terminar em uma casa diferente, diz-se que o problema é aberto.
No WebSite:
https://
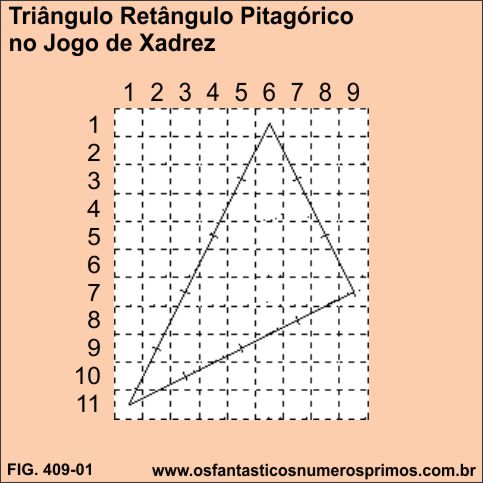
é apresentado o desenho da (Figura 409-01) o qual foi publicado em 1999 na Games and Puzzles Journal em sua edição de número 16, solicitanto ao leitor que descubrisse a área do triângulo formado por movimentos da peça do Cavalo do Jogo de Xadrez:
Harold James Ruthven Murray, mais conhecido como H. J. R. Murray (1868-1955), foi um educador britânico, inspetor de escolas e proeminente historiador de xadrez. Seu livro, A History of Chess, é amplamente considerado como a história mais confiável e abrangente do jogo.[2]
O desenho da (Figura 409-01) também aparece em uma das obras de Harold James Ruthven Murray que o descreve como um Triângulo Retângulo Pitágórico de proporção 3:4:5, pois ele verificou que os ângulos agudos são: 36° 52' 11.4" e 53° 7' 48.6".
Além dos ângulos agudos, cada lado do triângulo são traçados das seguintes formas:
Hipotenusa: 5 movimentos do Cavalo;
Cateto Maior; 4 movimento do Cavalo;
Cateto Menor: 3 movimentos do Cavalo
3, 4, e 5 são números inteiros que formam um terno pitagórico e estão estritamente relacionados com o Teorema de Pitágoras: a2 + b2 + c2.
Importante observar que o triângulo retângulo (com movimentos do Cavalo) só é possível de se construir porque a base do Xadrez de 8x8 casas (64) foi extendida para 9x11 casas (99).
Fonte: Adaptado de https://
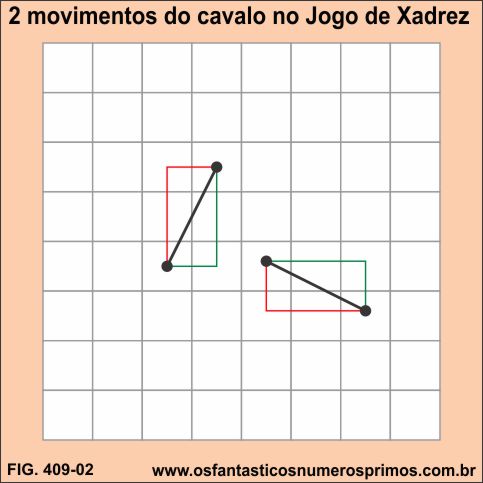
Efetuando-se 2 movimentos do Cavalo se chega ao ponto de partida do Cavalo.
O Cavalo é uma peça cujo movimento é duas casas em linha reta e virando-se uma casa a 90 graus, isto é, seu movimento se assemelha a letra éle (L). O Cavalo é a única peça que pode pular sobre as outras peças do Xadrez.
Com 2 movimentos do Cavalo, pode-se partir e chegar ao mesmo ponto de partida.
Os movimentos do Cavalo estão representado por éles (L) coloridos.
Unindo-se os pontos de partida e de chegada obtem-se um segmento de reta.
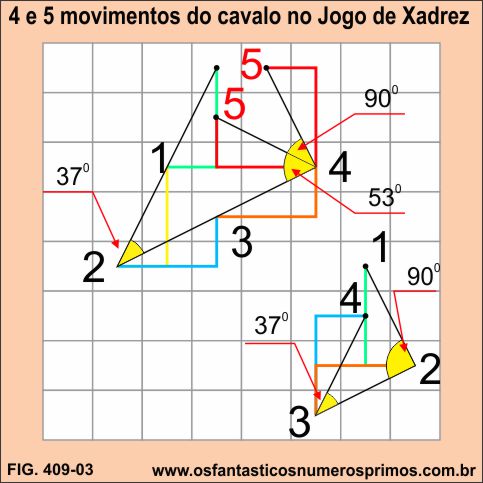
Efetuando-se 3 ou 5 movimentos do Cavalo não se consegue construir um triângulo.
Interessante observar que unindo-se o ponto de partida até quase a chegada, os seguimentos formam ângulos bastantes sugestivos de 37, 53 e 90 graus.
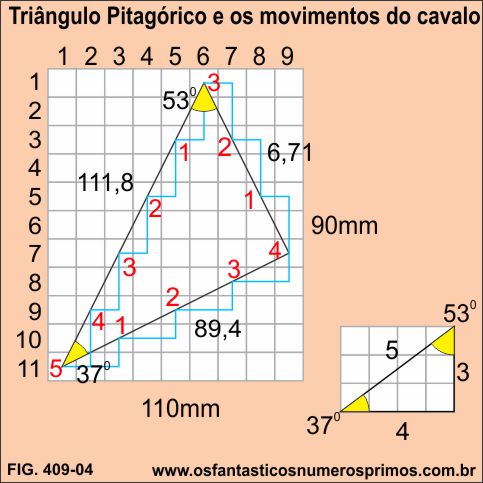
Efetuando-se 12 movimentos do Cavalo, consegue-se construir um Triângulo Retângulo Pitagórico conforme etapas a seguir:
Hipotenusa: 5 movimentos do Cavalo;
Cateto Maior: 4 movimento do Cavalo;
Cateto Menor: 3 movimentos do Cavalo
Os números das etapas dos movimentos realmente formam um Terno Pitágórico, pois são números inteiros.
Analisando com mais rigor o triângulo retângulo, não podemos dizer o mesmo das medidas que formam os seguimentos consecutivos, pois não são números inteiros.
Considerando os ângulos em números inteiros: 37 e 53, eles são os mesmos ângulos do Triângulo Retângulo Pitagórico 3-4-5.
Estamos diante de um caso geométrico sui generis e paradoxal, pois em um mesma construção geométrica têm-se um Triângulo Retângulo Pitagórico de proporção 3-4-5 cujas medidas de seus seguimentos dos seus lados não são números inteiros.
Autor: Ricardo Silva - dezembro/2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://
https://

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato