capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Divina Proporção Tipográfica (quadrilátero) - 511

Raul Mario Rosarivo (1903-1966) foi um tipógrafo, pesquisador, designer, poeta, pintor e ilustrador argentino, conhecido por seu trabalho na análise das Bíblias de Gutenberg. [1]

Em sua obra Divina Proporcion Tipográfica ele afirma que Módulos do Retângulo Pi, da Divina Proporção Tipográfica pode ser deduzidos por meio figuras geométricas como: triângulo retângulo, quadrilátero e circunferências.

Rosarivo cita também, que o meio mais simples é por meio da figura 7, no qual demonstra folha de papel dividida em vários formatos com suas respectivas áreas de manchas e margens proporcionais.

Página In-Fólio dividida em 2, 4, 8 e 16 partes

Fonte: https://issuu.com/ ruarfi/ docs/ rosarivo_dpt_1-46 ROSARIVO, Raul Mario. Divina Proporcion Tipografica. Ministerio de Eduacaion de La Provincia de Bueros Aires, La Plata, 1956

Rosarivo transcreve em seu livro, um artigo com estudos de Sebastian Duenas Blasco publicados na Revista técnica "Gráficas" de las técnicas del livro. Madri, ano X, no 107, pág. 223-224-240: Propriedades de los 3 cânones áureos em que são apresentados 3 "novos" métodos geométricos construir retângulos áureos de módulo 1,5.

Neste estudo é apresentado a construção Módulo Áureo por meio de quadrilátero.

Módulo Áureo (quadrilátero) - construção

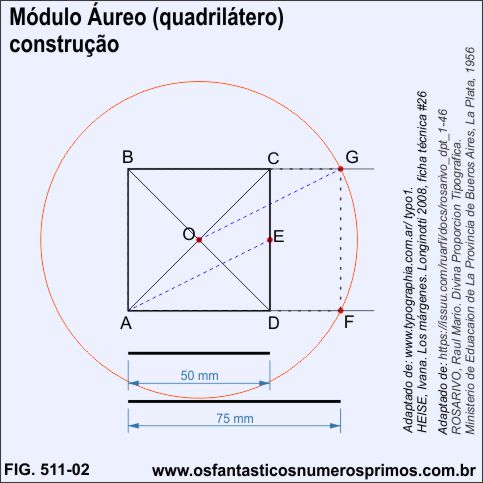
a) constrói-se um quadrilátero ABCD cujos lados medem 50mm;

b) determine o centro O;

c) determine o ponto médio E do lado CD;

d) ponta seca em A e abertura do compaço AE;

e) ponta seca em O, mesma abertura AE, intersecte os prolongamentos dos lado AD e BC, marcando os pontos F e G;

Desta forma se obtem um retângulo áureo ABGF de lados de 50mm x 75mm, razão de 2/3 em que a razão áurea tipográfica é 1,5 (contornos tracejados)

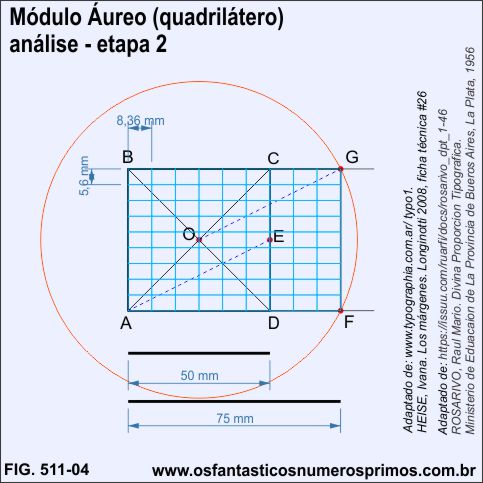
Módulo Áureo (quadrilátero) - construção

Módulo Áureo (quadrilátero) - análise - etapa 1

Inscrevendo-se uma malha quadriculada 3x3 sobre o quadrilátero ABCD, se obtêm outras informações da construção geométrica:

a) 1/3 do quadriculado tem a medida de 16,7mm;

b) 2/3 do quadriculado tem a medida de 33,36mm.

Dividindo-se 1/3 do quadriculado que é 16,7mm (módulo áureo) por 3, o quociente é 5,6mm .

Módulo Áureo (quadrilátero) - análise - etapa 2

Inscrevendo-se uma malha retangulada 9x9 (Cânone de Rosarivo) sobre o retângulo áureo, observa-se que as medidas de uma célula é de 5,6mm x 8,3mm.

5,6mm é 1/3 de 16,7mm (Módulo Áureo) para um quadrado de lados de 50x50mm.

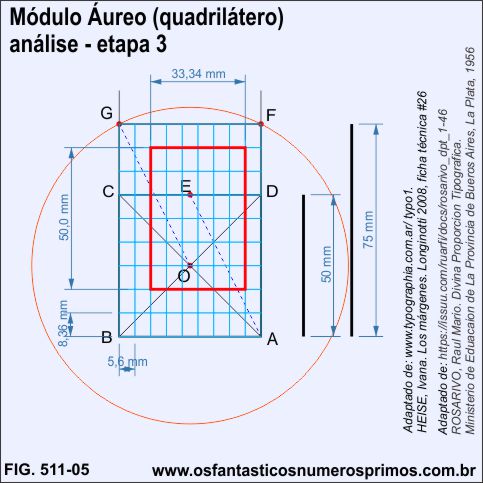
Módulo Áureo (triângulo retângulo isóceles) - análise - etapa 3

Posicionado-se a área de mancha (cor vermelha) no retângulo áureo obtem-se as dimensões das margens e da área mancha proporcionais ao módulo áureo quanto ao retângulo áureo.

a) a margem direita é o dobro (11, 2mm) da margem da lombada (5,6mm);

b) a margem inferior é o dobro (16,6mm) da margem superior (8,3mm).

c) a altura da área de mancha (50mm) corresponde a largura do retângulo áureo;

d) altura dividida pela largura no retângulo áureo: 75 / 50 = 1,5 (número áureo tipográfico);

e) altura dividida pela largura na área da mancha: 55 / 33,36 = 1,5 (número áureo tipográfico);

Autor: Ricardo Silva - agosto/2024

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

[1]https:// en.wikipedia.org/wiki/Ra%C3%BAl_Rosarivo

[2] https://issuu.com/ ruarfi/docs/rosarivo_dpt_1-46 ROSARIVO, Raul Mario. Divina Proporcion Tipografica. Ministerio de Eduacaion de La Provincia de Bueros Aires, La Plata, 1956.

[3]www.typographia.com.ar/ typo1. HEISE, Ivana. Los márgenes. Longinotti 2008, ficha técnica #26