


No desenvolvimento de projeto gráfico, diversas são as etapas para sua realização, tais como: briefing, rafes (esboços), lay-outs, artes-finais, provas de impressão (provas de prelo) , impressão, acabamento, enobrecimento, etc.
Uma das etapas de personalização de projeto gráfico é desenvolver a sua estrutura interna de design, isto é, elaborar o seu diagrama, também conhecido por Grade, Grid, Malha, Gabarito, Prancha, etc. onde serão dispostos a área de mancha (textos, títulos, ilustrações, etc), bem como números de páginas, seções, grafismos, margens, etc.
Malha, Grade, Grid, Gabarito, Gabarito de Diagramação, Prancha, podem receber um nome especial, denominado de Cânone da Construção de Páginas em que consiste obter página harmônica e esteticamente "perfeita" em relação as suas dimensões e com proporções agradáveis de área de mancha e margens.
Alguns cânones famosos são os de Villard de Honnecourt, de J. A. van de Graaf, popularizados por Jan Tschichold.
Jan Tschichold também criou o seu próprio cânone e divulgou o de Raul Mario Rosarivo.
Euclides de Alexandria, em sua obra Os Elementos, livro VI, define a divisão em média e extrema razão como:
"Um segmento de reta se diz dividido em média e extrema razão, se a razão entre o nenor e maior dos seguimentos é igual a razão entre o maior e o segmento todo".
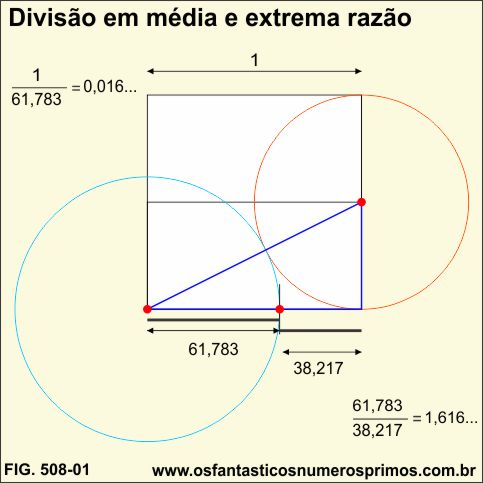
Um dos métodos geométricos de se determinar a divisão em média e extrema razão é por meio de um quadrado, vejamos:
a) dividi-se um quadrado ao meio;
b) constrói-se um triângulo retângulo escaleno (violeta), cuja base é o dobro da altura;
c) traça-se uma circunferência (laranja) cujo diâmetro é o lado direito do quadrado;
d) traça-se outra circunferência (azul), centro no vértice esquerdo inferior do quadrado com raio até a primeira circunferência (laranja);
e) a intersecção entre a circunferência (azul) com a base do triângulo retângulo escaleno (violeta), determina o ponto áureo.
Raul Mario Rosarivo (1903-1966) foi um tipógrafo, pesquisador, designer, poeta, pintor e ilustrador argentino, conhecido por seu trabalho na análise das Bíblias de Gutenberg. Ele ocupou o cargo de Diretor Geral dos Talleres Gráficos de la Provincia de Buenos Aires. [1]
Rosarivo, em sua Divina proporcion tipografica ("Proporção Divina Tipográfica"), publicada pela primeira vez em 1947, analisou livros renascentistas com a ajuda de compasso e régua e descreveu o uso do "número de oro" (número de ouro), pelo qual ele quis dizer a proporção 2:3, em livros produzidos por Gutenberg (assim como Peter Schöffer, Nicolas Jenson e outros). De acordo com o próprio Rosarivo, seu trabalho e afirmação de que Gutenberg usou o "número de ouro" (ou "número secreto", como Rosarivo também o chamou) para estabelecer as relações harmônicas entre as diversas partes de suas obras impressas, foi analisado por especialistas do Museu de Gutenberg e republicado no Gutenberg Jahrbuch, sua revista oficial. [1]
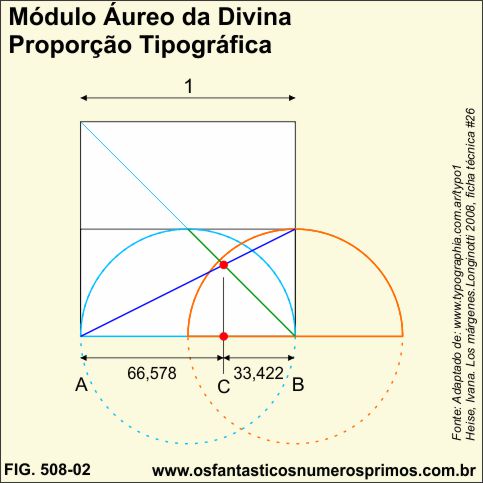
Para se construir o Módulo Áureo da Divina Proporção Tipográfica procedemos com as seguintes etapas:
a) construa duas semicircunferências (azul e laranja), com o centro na semicircunfência da outra;
b) traça-se um seguimento (violeta) do canto esquerdo inferior da semicircunfêrencia (azul) até o topo da semicircunfêrencia (laranja);
c) traça um segmento (verde) do centro da semicircunfêrencia (laranja) até o topo da semicircunfêrencia (azul);
d) AC e CB são os Módulos Áureos da Divina Proporção Tipográfica. (1,5 que é igual a 1,6 da medida tipográfica).
Interessante observar que na construção geométrica para obtenção dos Módulos Áureos da Divina Proporção Tipográfica está ímplícito a construção geométrica da Vesica Piscis.
Veja também que a construção geométrica pode ser realizada com um quadrado dividido ao meio, traçando-se a diagonal principal e um seguimento do ponto médio do lado direito até o vértice esquerdo inferior (sem uso de circunferências, bem como, da Vesica Piscis).
Fonte: Adaptado de: www.typographia.com.ar/
HEISE, Ivana. Los márgenes. Longinotti 2008, ficha técnica #26 [2]
O Módulo Áureo da Divina Proporção Tipográfica é exatamente 1/3 do lado do quadrado.
Sobrepondo-se uma malha quadriculada 3x3 (cor magenta) sobre a construção do Módulo Áureo da Divina Proporção Tipográfica, vê-se que um dos vértices da malha recai justamente sobre o ponto do Módulo Áureo.

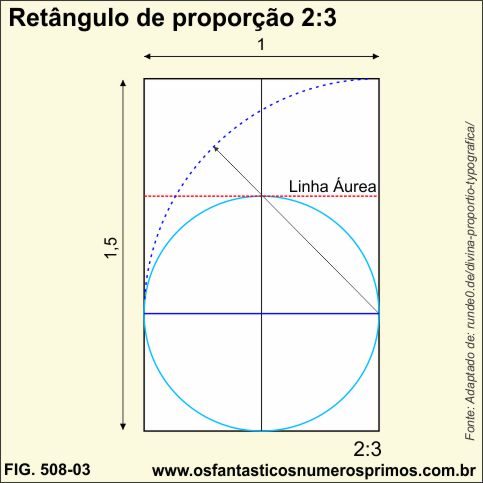
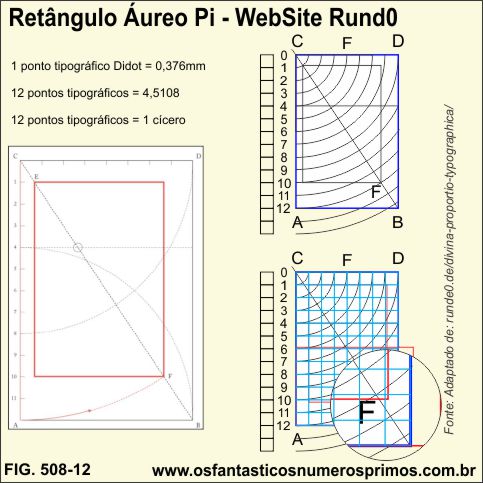
Transportar o diâmetro de uma circunferência inscrita em um quadrado a 90 graus, obtem-se um retângulo de proporção 2:3.
Fonte: Adaptado de: runde0.de/
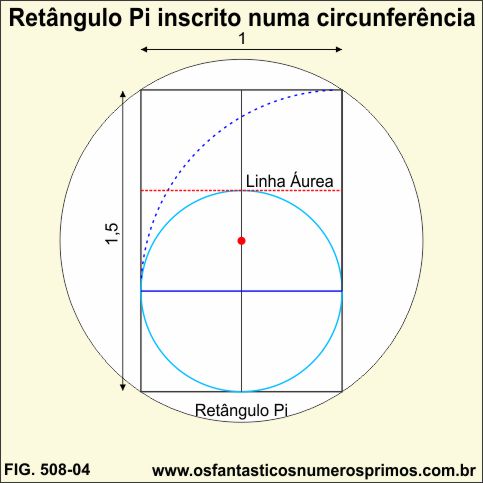
O Retângulo Pi de proporção 2:3, assim denominado por Raul Mario Rosarivo, pode ser inscrito numa circunferência.
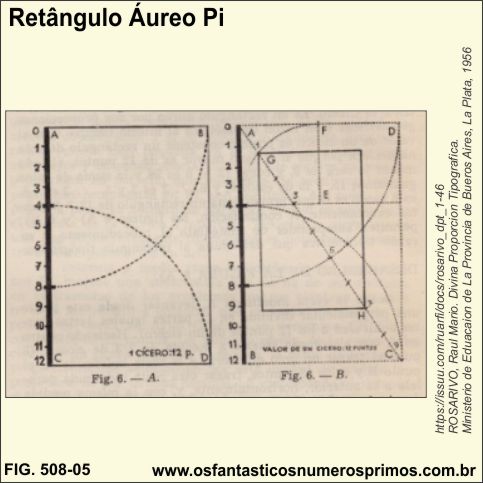
Fonte: https://issuu.com/
a) sobre uma reta indefinida, marque o ponto A e construa uma perpendicular dividida em 12 partes (cada parte é igual a 12 pontos tipográficos, equivalente a 1 cícero);
b) na parte 12 (12 cíceros), marque o ponto C;
c) centro em A, abertura de 2/3 de cícero (8 cíceros), traçar um arco cortando a reta indefinida e marcar o ponto B;
d) centro em C, mesma abertura de 2/3 de cícero, marque o ponto D.
Desta forma, se obtem um Triângulo Áureo Pi, de valor 1,6.

Como na figura 508-04 acima, pode se comprovar o Retângulo Áureo Pi, inscrevendo um quadrado (verde) no retângulo, inscrevendo uma circunferência (vermelha) no quadrado (verde) e depois projetando o diâmetro até o vértice D do retângulo.
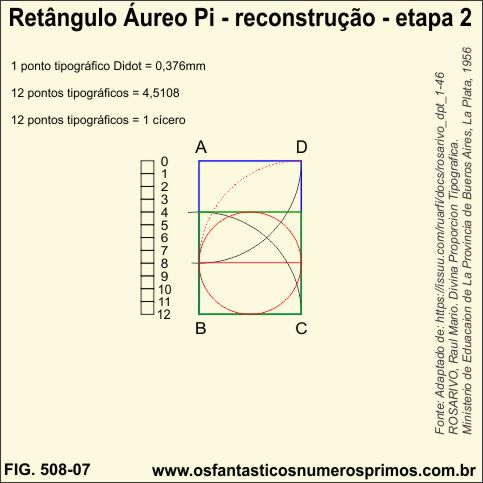
e) traçar a diagonal AC;
f) da medida 4 de cíceros, traçar uma paralela a AD e no ponto médio marcar o ponto E;
g) do ponto E, traçar um perpendicular e marcar o ponto F;
h) centro E, raio EF, marcar o ponto G na diagonal;
Observação muito importante: segundo o que está escrito no livro, o dobro do seguimento AG determina a margem direita da área da manha gráfica.
Girando a 90 graus o retângulo inscrito (vermelho), o seu lado maior não é a metade da largura do retângulo maior, há diferença no comprimento.
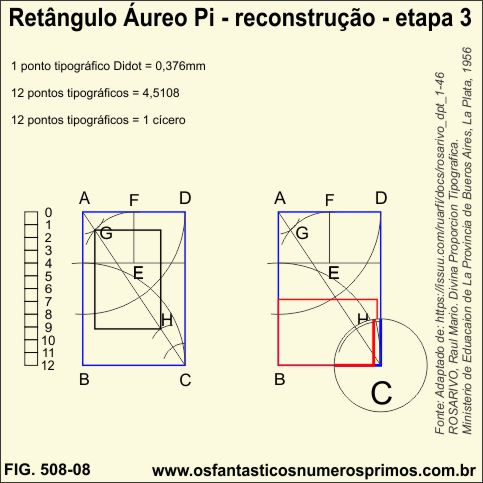
i) transportando o seguimento AG ao longo da diagonal do retângulo menor (área da mancha), a medida sai para fora do retângulo maior;
j) a diagonal do retângulo menor deveria conter 6 partes do seguimento AG, na realidade contêm 5,5 partes aproximadamente, diferentemente da construção original monstrada na figura 508-05 acima, extraída do livro de Rosarivo.
Inconsistência na construção geométrica original do livro ou na reconstrução demonstrada aqui no WebSite Os Fantásticos Números Primos ?

j) sobrepondo uma malha retangulada 9x9 (Cânone de Rosarivo), nota-se que a área da mancha (retângulo cinza) não se alinha no topo, na na base e nem na lateral direita sobre a malha retangulada.
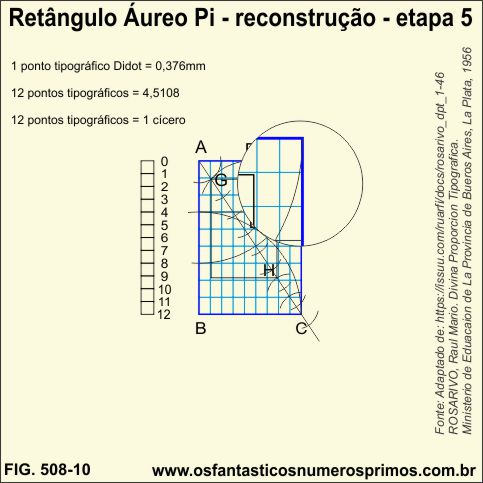
Observações:
a) um dos métodos para dividir um seguimento de reta em partes iguais com uso de compasso e régua não graduada é utilizar o Teorema de Tales - Feixe de Retas Paralelas.
b) atualmente com softwares aplicativos como CorelDraw (layout de página), InDesig (Diagramação), Photoshop (edição de imagem bitmap) e outros se constroem malhas quadriculadas ou retanguladas, etc., de quaisquer tamanhos, de forma que se pode dividir seguimentos ou áreas em partes iguais.
c) a seguir, será demonstrado o método de divisão de seguimento em partes iguais com o cânone de Villard de Honnecourt.
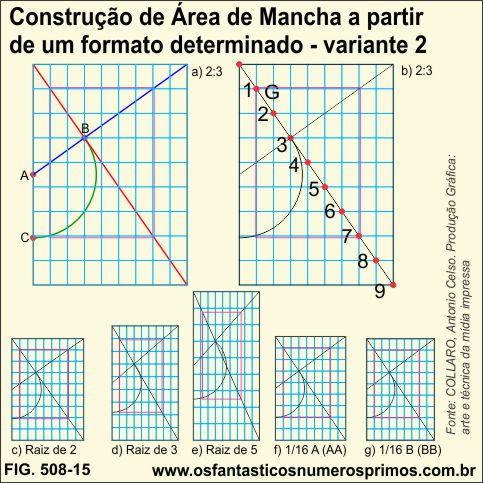
No capítulo 4 - Técnica e estética na produção de livros da obra Produção Gráfica: Arte e técnica da mídia impressa do autor Antonio Celso Collaro se encontra construção geométrica de construção de área de mancha semelhante a do livro de Raul Mario Rosarivo.
Observação importante: o seguimento AG, diferentemente do está escrito no livro, não corresponde a 1/9 da diagonal da página, pois é maior em seu comprimento.
Na verdade o seguimento AG é quase 1/8 da diagonal do triângulo (detalhe a).

Observações:
a) um dos métodos clássicos para dividir um seguimento de reta em partes iguais com uso de compasso e régua não graduada é utilizar o Teorema de Tales - Feixe de Retas Paralelas.
b) atualmente com softwares aplicativos como CorelDraw (layout de página), InDesig (Diagramação), Photoshop (edição de imagem bitmap) e outros se constroem malhas quadriculadas ou retanguladas, etc., de quaisquer tamanhos, de forma que se pode dividir seguimentos ou áreas em partes iguais.
c) a seguir, será demonstrado o método de divisão de seguimento em partes iguais com o cânone de Villard de Honnecourt.
Em um retângulo:
a) traçar uma diagonal (cor vermelha);
b) traçar um seguimento oblíquo do ponto médio de um dos lados até o vértice superior oposto (cor violeta);
c) traçar um arco, centro A, abertura AB, marcar o ponto C;
d) o ponto C determina a base do retângulo inscrito, isto é, a área de mancha.
Nesta variante de construção de área de mancha, sobrepondo malhas retanguladas 9x9, o formato 1/16 B derivado do Formato de Papel 66x96 (BB), é o único em que o contorno da área de mancha é sobreposta perfeitamente pela malha retangulada 9x9, nos demais formatos: de a) a f), isto não acontece.
Em todos os exemplos, vértices opostos das áreas de manchas, se encontram alinhados às diagonais dos formatos.
Os formatos 1/16 A e 1/16 B são os únicos em que às alturas das manchas se igualam as larguras das páginas.
No WebSite Runde Null, link: runde0.de/divina-proportio-typographica/, se encontra construção geométrica tendo como base o Retângulo Áureo Pi de Rosarivo.
O autor tenta dividir a diagonal do Retângulo Áureo em partes iguais utilizando-se de arcos concêntricos.
A divisão da diagonal é aproximadamente 14,5 partes, medida esta, não inteira.
O autor afirma que o retângulo (área da mancha) inscrito tem proporção 6:9.
Inscrevendo-se uma matriz retangulada de 8x12, observa-se que o retângulo inscrito não tem exatamente a proporção 6:9 e também não se alinha com o retangulado.
Rotacionando o retângulo em 90 graus, observa-se o seu lado maior não corresponde ao comprimento do lado menor do Retângulo Áureo Pi.
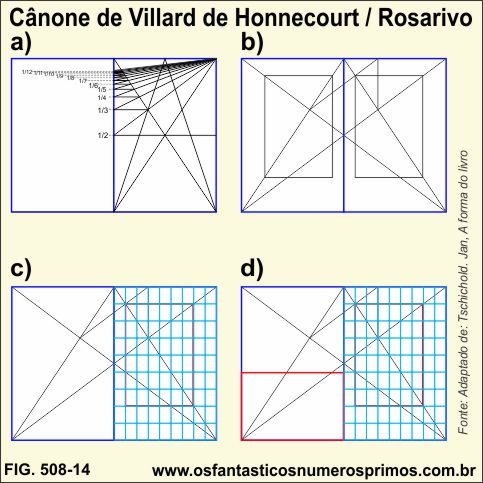
Segundo Jan Tschichold, em sua obra A Forma do Livro:
"Este cânome gôtico, quase desconhecido até aqui e verdadeiramente emocionante, redunda em divisões harmoniosas e pode ser traçado dentro de qualquer retângulo"
"Usando o o cânone de Villard, ..., é possível dividir uma linha reta em qualquer número de partes iguais sem a necessidade de um instrumento de medição"
Interessante notar a frase: "sem a necessidade de um instrumento de medição", frase esta que remete a construções geométricas por meio da Vesica Piscis como também da Mandorla e que não precisam de instrumentos de medições.
a) constrói-se dois retângulos de proporções de 2:3 (cor violeta);
b) traçam-se duas diagonais maiores (cor magenta);
c) traçam-se duas diagonais menores (cor verde);
d) na intersecção das duas diagonais (magenta e verde) na parte direita, traça-se uma perpendicular (cor azul) até o topo;
e) traça-se um seguimento oblíquo (cor laranja);
f) na intersecção do seguimento (laranja) com a diagonal (verde) na parte direita, inicia-se o traçado da área da mancha (retângulo cinza).

detalhe a) folha em formato 2:3 dividida pelo cânone de Villard de Honnecourt em várias partes;
detalhe b) áreas de manchas obtida por meio do cânone de Villard de Honnecourt;
detalhe c) sobrepropondo-se o cânone de Rosarivo (malha retangulada 9x9) sobre o cânone de Villard de Honnecourt, o retângulo inscrito de Villard é idêntico ao de Rosarivo;
detalhe d) rotacionando a área de mancha (retângulo inscrito), o seu maior lado é igual ao menor lado do retângulo de proporção 2:3.
Nos exemplos a seguir, cânones de Villard de Honnecourt, Raul Maio Rosarivo, Jan Tschichold e J. A. van de Graaf sobrepostas às páginas da Bíblia.
Interessante observar que vértices das áreas de manchas se alinham perfeitamente às diagonais dos cânones.




Autor: Ricardo Silva - julho/2024
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[1]https://
[2]www.typographia.com.ar/
[3]runde0.de/

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato