


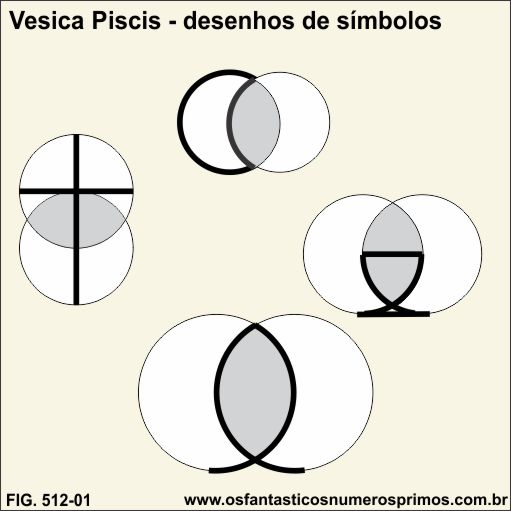
Vésica Piscis é uma construção geométrica com duas circunferências de mesmo raio na qual o centro de uma está sobre a circunferência da outra.
Na intersecção das duas cincunferências é possível obter desenhos de símbolos como: cruz, lua, taça, entre outros, e principalmente a figura de bexiga de peixe.
A partir da Vesica Piscis são possíveis de se construirem série de polígonos cujos lados possuem mesma medida.
Arquitetos, desenhistas, mestres pedreiros e pintores, como Thomasim Von Zirclaere, Villard de Honnecourt, Mathes Roritzer, Leonardo da Vinci, Sebastiano Serlio, Antonio Rodrigues, Albrecth Durer fizeram uso da Vesica Piscis tanto em trabalhos arquitetônicos e artísticos como em estudos geométricos.[1]
Segundo Felipe Alberto da Silva:"O método da Vesica Pisces não necessita de qualquer cálculo ou medição. É um método ideal para deixar fluir a intuição do artista sem esta entrar no costrangimento de um raciocínio analítico".[1]
Para mais informações sobre a Vesica Piscis, veja abaixo, matérias relacionadas!
Em sua obra: A Forma da Livro, Jan Tschichold faz a seguinte afirmação: "usando o cânone de Villard de Honnecourt, é possível dividir uma reta em qualquer números de partes iguais sem necessidade de um instrumento de medição"[2]
O presente estudo demonstra relações geométricas e numéricas entre a Vesica Piscis com o cânone de construção de páginas desenvolvido por Raul Mario Rosarivo.
a) centro em D, traçar uma circunferência e marcar o diâmetro AB;
b) centro B, traçar outra circunferência de mesmo raio;
c) a partir de B, traçar um seguimento perpendicular e marcar o ponto C na intersecção com a segunda circunferência;
d) centro em C, raio AD, marcar o ponto E na intersecção com a primeira circunfefência;
e) traçar os seguimentos AC e BE e na intersecção, marcar o ponto F;
Os seguimentos AF e FC são Módulos Áureos da Divina Proporção Tipográfica. (1,5 que é igual a 1,6 da medida tipográfica).
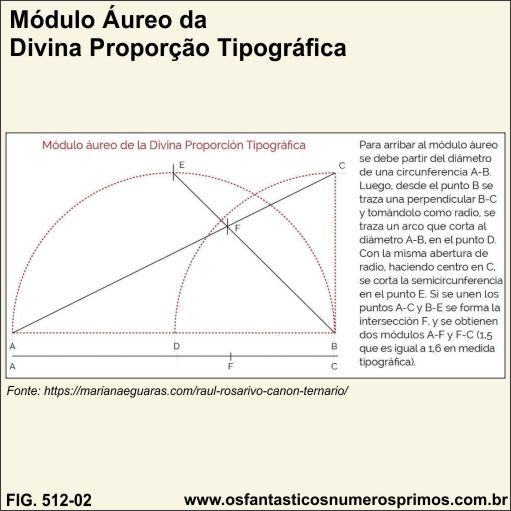
Refazendo a construção geométrica do Módulo Áureo da Proporção Tipográfica, vê-se claramente a intersecção e sobreposição de duas circunferências, isto é, a própria Vesica Piscis.
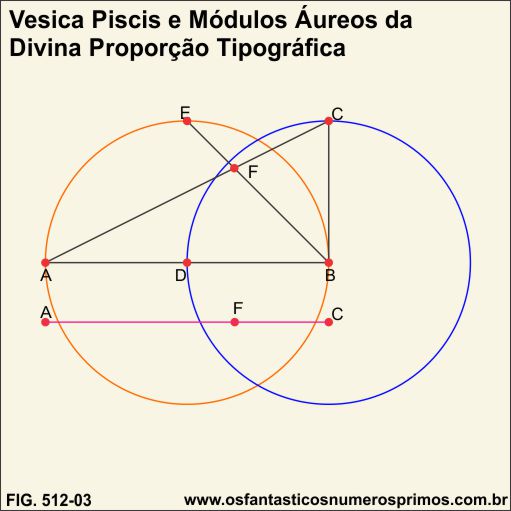
Construíndo-se um quadrado (cor verde) cujos lados são o seguimento AB; prolongando o seguimento BE, forma-se a diagonal do quadrado, o seguimento AC parte do vertice esquerdo inferior até o ponto médio do lado direito do quadrado, demonstrando-se desta forma que os Módulos Áureos da Divina proporção tipográfico também podem ser contruídos por meio de quadrado e triângulo retângulo escaleno ABC cuja base é o dobro da altura.
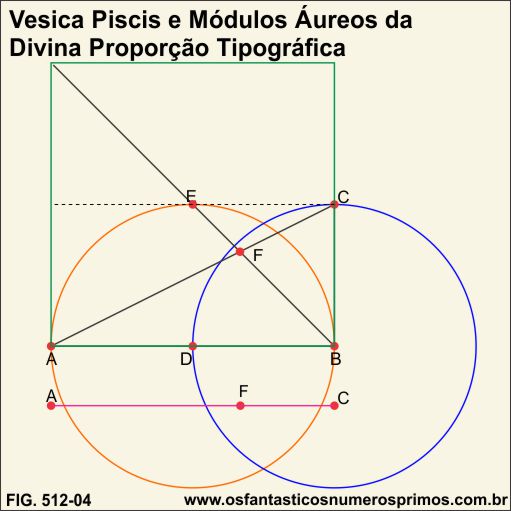
Sobrepondo-se uma malha quadriculada (cor azul) sobre o quadrado da construção de Módulos Áureos (cor verde), ve-se que um dos vértices da malha quadriculada recai justamente sobre o ponto F.
O seguimento FC corresponde a 1/3 do lado do quadrado.
O seguimento AF corresponde a 2/3 do lado do quadrado.
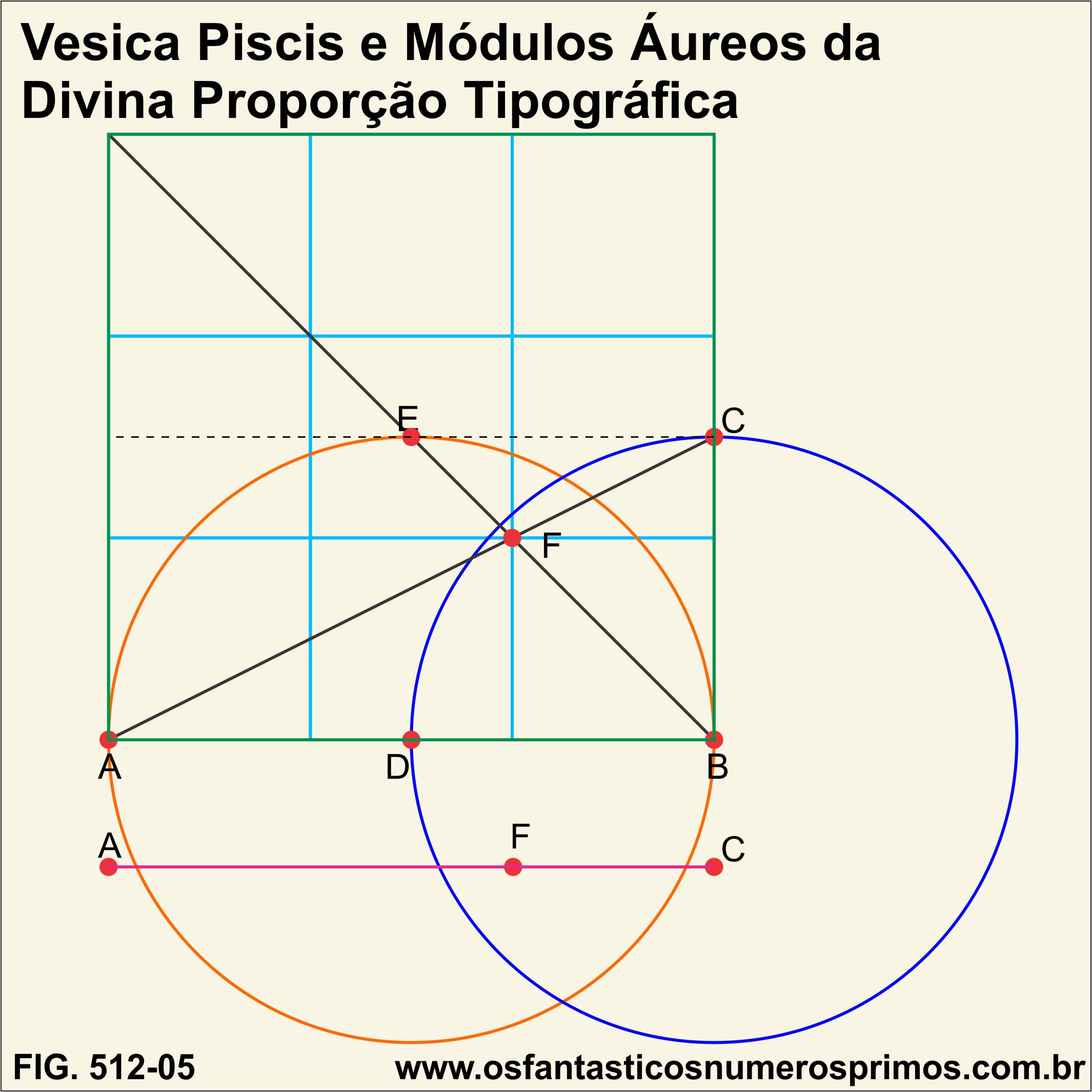
Por meio da Vesica Piscis é possível determinar seguimentos de 1/3 e 2/3 de um quadrado o qual foi comprovado com a sobreposição de uma malha quadriculada 3/3.
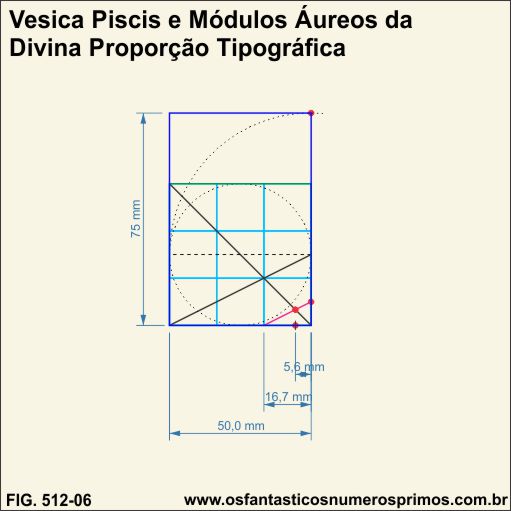
Utilizando-se do mesmo método, encontra-se 1/3 de uma célula do quadridulado no canto direito inferior cuja medida é 5,6mm.
1/3 da malha quadriculada é igual a 16,7mm (módulo áureo).
1/3 de 16,7 é igual a 5,6mm.
Increvendo-se uma circunferência no quadrado (cor verde) e transportando o diâmetro para o lado direito e posteriomente prolongando os lados do quadrado obtem um retângulo de proporção de 2/3, denominado por Raul Mario Rosarivo de Retângulo Áureo Pi.
Inscrevendo-se a malha retangulada de 9x9 (Cânone de Rosarivo) no retângulo de proporção 2:3 (50mm x 75mm) e a área de mancha (cor vermelha), obtem-se a Divina Proporção Tipográfica, vejamos:
a) Formato da folha: 50mm x 75mm - proporção de 2:3;
b) Formato da área de manha: 33,3mm x 50mm - proporção de 2:3;
c) a altura da mancha corresponde a largura da folha - 50mm;
d) a margem direita é 2 x 5,6mm da margem da esquerda (lombada);
c) a margem inferior (pé) é 2 x 16,7mm da margem superior (cabeça).
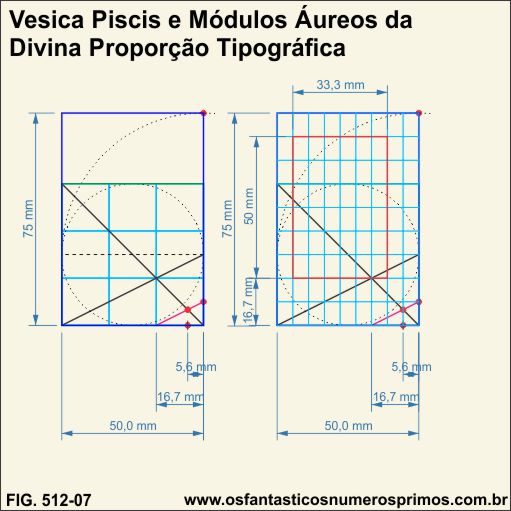
As divisões do quadrado em 1/3 e novamente em 1/3, demonstra que uma célula de um retangulado 9x9 corresponde a 1/9 do Cânone de Rosarivo.
A divisão de uma página de proporção 2:3 com um retangulado de 9x9 células estabelece proporções harmônicas entre margem direita e esquerda, entre margem inferior e superior, bem como, a área de mancha com o formato de página.
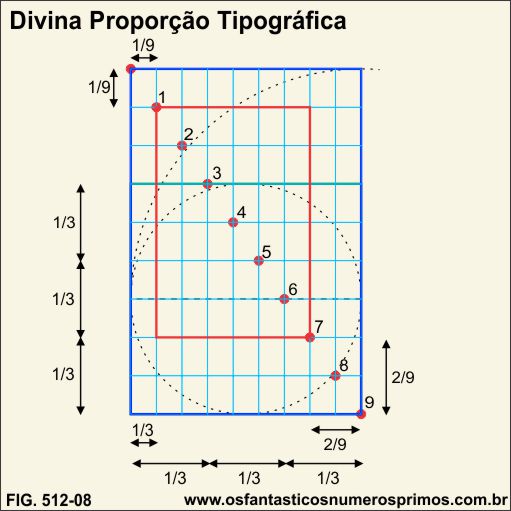
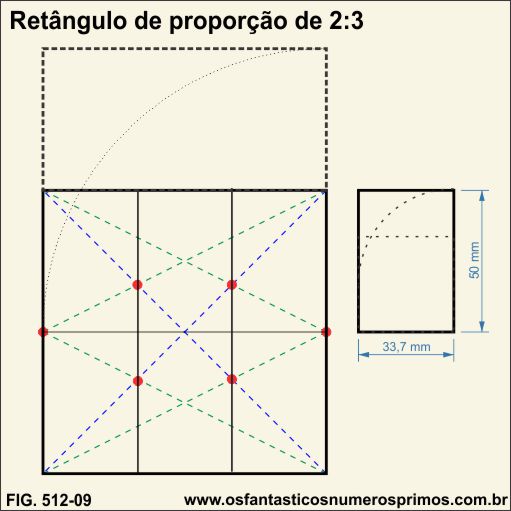
Retângulo de proporção de 2:3 também pode ser obtido por meio da seguinte construção geométrica:
a) traçam-se as diagonais do quadrado;
b) traçam-se seguimentos oblíquos do ponto médio dos lados até o vértice oposto;
c) traça-se um seguimento horizontal dividindo o quadrado ao meio;
d) traçam-se seguimentos verticais nas intersecções das diagonas com seguimentos oblíquos.
Desta forma, o quadrado fica dividido em 6 retângulos de proporção 2:3.
De forma mais prática ainda, um quadrado mais a sua metade gera um retângulo de proporção 2:3
Autor: Ricardo Silva - agosto/2024
[1] SILVA, Felipe Alberto da. A figura da Mandorla e da Vesica Pisces - As possilibilidades de construção - Dissertação de Mestrado. Universidade de Lisboa - Faculdade de Belas Artes, 2013.
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
[2] TSCHICHOLD, Jan. A Forma do Livro. tradução de José Laurêncio de Melo. Atelie Editorial
https://marianaeguaras.com/

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato