


Você resolve fazer uma brincadeira, um desafio, com parentes, amigos ou com seus alunos.
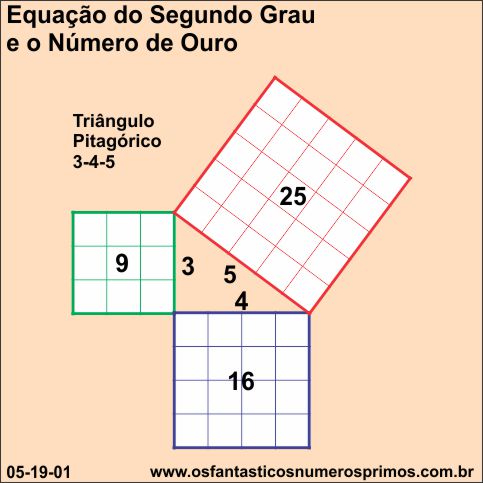
Você tem em mãos uma folha de papel quadriculado, recorta 3 quadrados; o primeiro, um quadrado de lado de 5 quadradinhos, o segundo, de lado de 4 quadradinhos e o terceiro, de lado de 3 quadradinhos.
O desafio é montar um triângulo retângulo com os 3 quadrados, você estipula um tempo, e o desafio então começa.
Com uma simples brincadeira, você tem a oportunidade de explicar o Teorema de Pitágoras de uma forma lúdica de que a soma de todos os quadradinhos do quadrado de lado 4, mais a soma de todos os quadradinhos do quadrado de lado 3 é igual a soma de todos os quadradinhos do quadrado de lado 5.
Agora é o contrário, desafiam você a provar a razão áurea, o número de ouro com uma folha de papel quadriculado, sem utilizar compasso ou régua.
Então, você pensa, pensa, fica matutando com os seus botões, queimando neurônios.
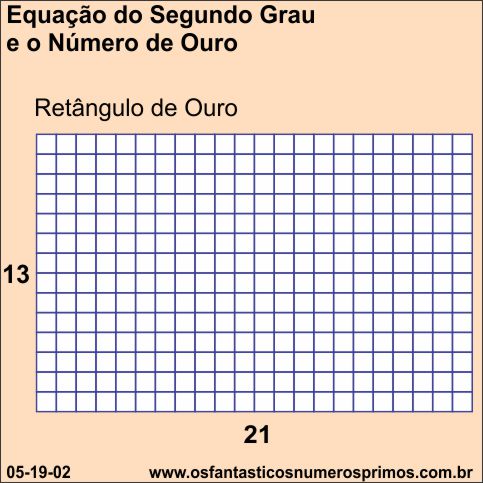
Sim, é isso mesmo, lógico !, na certa !, utilizarei números da Sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21,...
Corta um retângulo de 21 quadradinhos de comprimento por 13 quadradinhos de altura, tudo certo !
E aí, pedem para você provar porquê você utilizou esses números, porquê que você fez uso de Números de Fibonacci.
Cálculos terão que serem feitos ou em papel, ou em calculadora, ou em celular.
Você terá que mostrar e explicar que a razão entre um número e seu antecedente da Sequência de Fibonacci tende ao Número Phi (Ф), também conhecido como Número de Ouro, Razão Áurea, Razão Dourada: 1,618033657...
Lembro-me que na antiga 8a série do Primeiro Grau (hoje Nono Ano do Ensino Fundamental), tacavam e tacavam Fórmula de Bháskara (para nós brasileiros) e diziam que era uma fórmula muito importante e que seria muito utilizada no Segundo Grau (hoje Ensino Médio).
Cursei Segundo Grau Técnico de Publicidade e nada de Bháskara, Cursei Superior Publicidade e Propaganda e nada de Bháskara.
Por muito tempo, custou-me a entender a dinâmica e a lógica de utilização da Fórmula Geral de Resolução da Equação de Segundo Grau (Fórmula de Bhaskara, para nós brasileiros), eu me perguntava, como é que chegaram a tal fórmula para se resolver equações de segundo grau.
Digo isto, porque, através dela, de forma sintetizada, pode-se resolver tanto equações completas como equações incompletas do segundo grau sem a necessidade de se utilizar Fatoração, Fator em Evidência, etc.
Uma pesquisa aqui, outra acolá, encontrei na World Wide Web duas excelentíssimas séries de vídeo-aulas:
Curso de Aperfeiçoamento para Professores de Matemática do Ensino Médio
data: 26/28 de janeiro de 2004
Professor: Elon Lages de Lima (1929-2017)
Equação de Segundo Grau (parte I)
Equação de Segundo Grau (parte II)
Nas aulas, o Prof. Elon discorre sobre a História da Equação do Segundo Grau e apresenta problemas com resolução por meio de Fatoração e Método de Completar Quadrados.
e
Matemática do Vestibular
8 vídeo-aulas
Professor: Bruno Fraga Ferreira
data:
Nas aulas, o Prof. Bruno demonstra várias resoluções de Equações do Segundo Grau por meio de Fatoração, Completar Quadrados, Fator em Evidência sem utilização da Fórmula de Bhaskara e diz que em outros países ensinam-se primeiro os métodos por Fatoração, Completar Quadrados, Fator em Evidência, etc., e posteriormente a Fórmula Geral de Resolução de Equação do Segundo Grau.
Confesso ver e rever essas vídeo-aulas para ficar ainda mais afinado no entendimento de Equações do Segundo Grau.
Quanto menos se espera e num piscar de olhos, aparecem problemas e aplicações onde se tem que utilizar Equações do Segundo Grau.
E uma dessas aplicações é justamente encontrar o Número de Ouro 1,618033657...
A princípio nomes como Número de Ouro, Razão Dourada, Número Dourado, Número Fhi e tem até uma letra grega para representá-lo (Ф) em homenagem ao arquiteto grego Fhideas que projetou o Partenon, apareceram a partir da época do Renascimento.
Um método geométrico simples é determinar um segmento de reta e dividí-lo e duas partes.
Euclides de Alexandria os denominou de Média e Extrema Razão, autor de Os Elementos onde se encontram publicadas diversas outras formas por meio de figuras e construções geométricas de se encontrar a razão áurea.
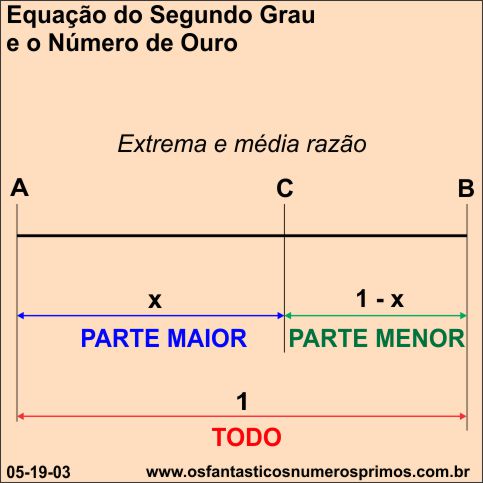
Com um segmento de reta AB e de medida de 1 unidade, marque um ponto C.
O ponto C divide o seguimento AB em média e extrema razão, isto é, a razão entre o seguimento TODO e a parte MAIOR é igual a razão entre a parte MAIOR e a parte MENOR.
Entre Livros, Teses de Mestrados, Ensaios e publicações afins que discorrem sobre o tema Número de Ouro, uma parte utilizam a Fórmula de Bháskara e outras a sugerem para a resolução da equação para se obter o Número de Ouro, isto é, são raras as publicações em que as etapas da Fórmula de Bháskara são mostradas completas ao leitor.
| - b ± √b 2 - 4 . a .c | ||
| x | = | _____________ |
| 2.a |
| Δ = b2 - 4 . a . c |
i)
Efetua-se a proporção onde o produto dos extremos é igual ao produtos dos meios.
| 1 | x | |
| ____ | = | ____ |
| x | 1 - x |
ii)
| x 2 | = | 1 - x |
iii)
Monta-se a Equação do Segundo Grau na forma completa : ax2 + bx + c = 0.
| x2 + x - 1 | = | 0 |
iv)
Aplicando Delta (Discriminante da equação)
| Δ = 12 - 4 . 1 ( - 12) |
v)
| Δ = 1+ 4 |
vi)
O Delta é maior que 0, portanto, há duas raízes.
| Δ = 5 |
vii)
| -1 ± √5 | ||
| x | = | _____________ |
| 2 |
viii)
Solução positiva.
| - 1 + √5 | ||||
| x' | = | _____________ | = | 1,6180 |
| 2 |
| - 1 + 2,236.. | ||||
| x' | = | _____________ | = | 1,6180 |
| 2 |
ix)
Solução negativa.
| - 1 - √5 | ||||
| x'' | = | _____________ | = | - 0,6180 |
| 2 |
| - 1 - 2,236 | ||||
| x'' | = | _____________ | = | - 0,6180 |
| 2 |
Aplicação do Método de Completar Quadrados para se obter o Número de Ouro.
O Método de Completar Quadrados é extremamente simples, como diz o Prof. Bruno Fraga Ferreira, em uma de suas vídeo-aulas.
Realmente, apresenta etapas à mais, mas praticando e pegando a dinâmica do processo é um método bastante eficiente.
i)
Efetua-se a proporção onde o produto dos extemos é igual ao produtos dos meios.
| 1 | x | |
| ____ | = | ____ |
| x | 1 - x |
ii)
| x 2 | = | 1 - x |
iii)
Monta-se a Equação do Segundo Grau na forma ax2 + bx + c = 0.
O termo "x2" possui coeficiente 1 e isto é um facilitador para se trabalhar com o Método de Completar Quadrados.
| x2 + x - 1 | = | 0 |
iv)
Desloque o termo "c" para o segundo membro, não esquecendo de trocar o sinal.
| x2 + x | = | 1 |
v)
| x2 | + | x | = | 1 |
vi)
Divida por 2 o termo "b", como é impar ele fica (1/2), faça a conta mentalmente, lembre-se que x é o mesmo que 1x.
| x | ||||
| x2 | + | ___ | = | 1 |
| 2 |
vii)
Eleve ao quadrado a fração (1/2)2.
O resultado é 1/4.
Coloque 1/4 a frente do termo x, somando-o.
Some também a fração 1/4 ao segundo membro, para equilibrar a equação.
| 1 | 1 | |||||||
| x2 | + | x | + | ___ | = | 1 | + | ___ |
| 4 | 4 |
viii)
Determine o Mínimo Múltiplo Comum e efetue a adição das frações.
| x2 | x | 1 | 1 | 1 | ||||
| ___ | + | ___ | + | ___ | = | ____ | + | ___ |
| 4 | 4 | 4 | 4 | 4 |
ix)
No primeiro membro aparece um Trinômio Quadrado Perfeito.
Fatore o primeiro membro da equação...
| 4x2 | + | 4x | + | 1 | = | 4 | + | 1 |
x)
...para obter o quadrado de uma soma (Produto Notável).
| ( 2 x + 1 ) 2 | = | 5 |
xi)
Extraia a raiz quadrada do dois membros da equação.
| 2 x + 1 | = | ± √5 |
xii)
| 2 x | = | ± √5 - 1 |
xiii)
Solução positiva.
| + √5 - 1 | ||||
| x'' | = | ____ | = | 1,6180 |
| 2 |
xiv)
Solução negativa.
| - √5 - 1 | ||||
| x' | = | ____ | = | 0,6180 |
| 2 |
Autor: Ricardo Silva - maio/2020
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
ALENCAR, Maria Efigênia Gomes de. O Número Phi e a Sequência de Fibonacci. Física na Escola, v. 5, n. 2, 2004
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato