capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Sequências de Fibonacci semelhantes - 254

Imagine que você esteja caminhando e resolve contar a quantidade de passos: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..., você poderiar estar recitando os números ou contando mentalmente.

Você resolve mudar a forma de contagem, começa então a contar: 1, 2, 4, 8, 16, 32, 64, 128, 256,...

São duas sequências numéricas com características diferentes:

a) a primeira é uma progressão aritmética (P.A.), em que cada termo, a partir do segundo, é igual ao anterior somado de uma constante chamada de razão, no exemplo, a diferença entre os termos é de 1 unidade;

Progressão Aritmética (P.A.)

1		2		3		4		5		6..
	+ 1		+ 1		+ 1		+ 1		+ 1

b) a segunda é progressão geométrica (P.G.), em que cada termo, a partir do segundo, é ígual ao anterior multiplicado por uma constante chamada de razão, no exemplo razão 2. Cada número posterior dobra de valor.

Progressão Geométrica (P.G.)

1		2		4		8		16		32..
	x 2		x 2		x 2		x 2		x 2

Tanto uma PA quanto uma PG, podem ter outras classificações como: sequência finita, sequência infinita, crescente, decrescente, estacionária, etc.

Sequência de Fibonacci

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,... é uma sequência numérica diferente de uma PA e uma PG, a partir do terceiro número, somando-se dois números precedentes tem como resultado o número posterior, ela é formada por recorrência.

O nome Sequência de Fibonacci foi uma homenagem feita por François-Édouard-Anatole Lucas (1842-1891), matemático francês, grande estudioso das obras de Leonardo Fibonacci, também conhecido como Leonardo Pisano, Leonardo de Pisa, Leonardo Bonacci. Foi Édouard Lucas quem notou que a soma de dois números tinha como resultado o próximo número da sequência.

François-Édouard-Anatole Lucas descobriu diversas propriedades numéricas e algébricas na Sequência de Fibonacci, a Sequência de Lucas é originada da Sequência de Fibonacci.

A Sequência de Fibonacci está publicada no livro Liber Abaci a qual está relacionada ao problema dos coelhos, isto é, a partir de um casal de coelhos, quantos coelhos terão depois de um ano, não havendo mortes ou doenças.

A Sequência de Fibonacci possui uma propriedade muito especial que foi observada por Johannes Kepler, astronômo, astrólogo e matemático alemão, que a divisão de um termo por um anterior, quanto mais se avança na sequência, tende ao número de ouro 1,6180339887 498948 48...

Sequência de Fibonacci	Número de Ouro (Ф)

	razão entre
	os termos
1	1
1	2
2	1,5
3	1,666666667
5	1,604984472
8	1,618033989
13	1,618033989
21	1,618033989
34	1,618033989
55	1,618033989
89	1,618033989
144	1,618033989
233	1,618033989
377	1,618033989
610	1,618033657

Sequência de Fibonacci e sequências derivadas

H. E. Huntley, em seu livro A divina Proporção, Cap. IV, pag. 54 diz que o número (phi) possuí o "dom" de aparecer inesperadamente nos lugares mais estranhos, pois qualquer sequência numérica cujo termo seja a soma de dois temos anteriores, a razão entre quaisquer dois termos dessa sequência tenderá para o Número phi (Ф), dando como exemplo a escolha de dois número aleatórios: 5 e 2 e formando a sequência: 5, 2, 7, 9, 16, 25, 41, 66,...

Sequência	razão entre
	os termos
5
2	0,4
7	3,5
9	1,285
16	1,777
25	1,562
41	1,64
66	1,609
107	1,621

No exemplo de H. E. Huntley, o número 2 estando como primeiro termo da sequência, as razões também tende ao o Número phi (Ф), Número de Ouro.

Sequência	razão entre
	os termos
2
5	2,5
7	1,4
12	1,71
19	1,58
31	1,631
50	1,612
81	1,62
131	1,617

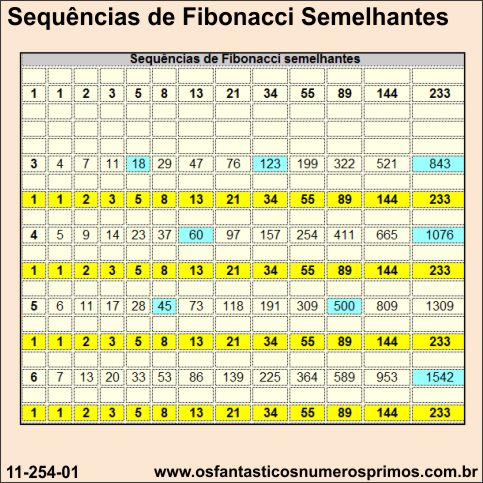
Formando sequências numéricas cujos dois primeiros termos são números consecutivos, primos entre si e aplicando a soma de dois termos anteriores, obtem-se sequências numéricas semelhantes à Sequencia de Fibonacci.

As diferenças entre termos correspondentes tem como resultado a Sequência de Fibonacci (linhas amarela).

A razão entre um termo e seu antecedente de cada sequência tende ao número de ouro.

Exemplos:

843 : 521 = 1,6180422264875239923224568138196

1076 : 665 = 1,618045112781954887218045112782

1309 : 809 = 1,61804697156983930778739184178

Sequências de Fibonacci semelhantes

1	1	2	3	5	8	13	21	34	55	89	144	233



3	4	7	11	18	29	47	76	123	199	322	521	843

1	1	2	3	5	8	13	21	34	55	89	144	233

4	5	9	14	23	37	60	97	157	254	411	665	1076

1	1	2	3	5	8	13	21	34	55	89	144	233

5	6	11	17	28	45	73	118	191	309	500	809	1309

1	1	2	3	5	8	13	21	34	55	89	144	233

6	7	13	20	33	53	86	139	225	364	589	953	1542

1	1	2	3	5	8	13	21	34	55	89	144	233

7	8	15	23	38	61	99	160	259	419	678	1097	1775

1	1	2	3	5	8	13	21	34	55	89	144	233

8	9	17	26	43	69	112	181	293	474	767	1241	2008

1	1	2	3	5	8	13	21	34	55	89	144	233

9	10	19	29	48	77	125	202	327	529	856	1385	2241

1	1	2	3	5	8	13	21	34	55	89	144	233

10	11	21	32	53	85	138	223	361	584	945	1529	2474

www.osfantasticosnumerosprimos.com.br