


A Sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,... é formada com a repetição do número 1 duas vezes e a partir do terceiro termo soma-se com o antecessor, ela apareceu em um problema em que se desejava saber o crescimento de população de coelhos e foi publicada no livro Liber Abacci - Livro do Ábaco ou do Cálculo - (1202) de autoria de Leonardo de Pisa (1175-?), conhecido como Fibonacci.
François-Édouard-Anatole Lucas (1842-1891), matemático francês e estudioso das obras de Leonardo de Pisa foi quem popularizou os Números de Fibonacci e que através dela criou outra sequência semelhante chamada de Sequência de Lucas: 2, 1, 3, 4, 7, 11, 18,...
Terno Pitagórico é uma sequência de três números inteiros que satisfazem o Teorema de Pitágoras, onde (a2= b2 + c2) - O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
a=m2 - n2
b=2mn
c=m2 + n2
onde:
m > n (m tem que ser maior que n)
m e n (tem que ser primos entre si, into é, o mdc é igual a 1)
Observação 1: dois números consecutivos são primos entre si.
Observação 2: as Fórmulas de Euclides não geram ternos pitagóricos derivados ímpares, elas geram o dobro, do dobro, do dobro de um terno pitagórico primitivo, estudos estes publicados no livro digital Ternos Pitagóricos e Sequências Numéricas.
Exemplo 1)
2 e 1
a= 22 - 12 = 4 - 1 = 3
b= 2 . 2 . 1 = 4 . 1 = 4
c= 22 + 12 = 4 + 1 = 5
3, 4 e 5 é um Terno Pitagórico Primitivo.
Exemplo 2)
3 e 2
a= 32 - 22 = 9 - 4 = 5
b= 2 . 3 . 2 = 6 . 2 = 12
c= 32 + 22 = 9 + 4 = 13
5, 12 e 13 é um Terno Pitagórico Primitivo.
Entre várias propriedades matemáticas, com a Sequência de Fibonacci também são possíveis de se gerarem ternos pitagóricos.
Primeiros 54 termos da Sequência de Fibonacci.
| Sequência de Fibonacci | |
|---|---|
| Ordem / | Números de Fibonacci |
| Posição | |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1.597 |
| 18 | 2584 |
| 19 | 4.181 |
| 20 | 6.765 |
| 21 | 10.946 |
| 22 | 17.711 |
| 23 | 28.657 |
| 24 | 46.368 |
| 25 | 75.025 |
| 26 | 121.393 |
| 27 | 196.418 |
| 28 | 317.811 |
| 29 | 514.229 |
| 30 | 832.040 |
| 31 | 1.346.269 |
| 32 | 2.178.309 |
| 33 | 3.524.578 |
| 34 | 5.702.887 |
| 35 | 9.227.465 |
| 36 | 14.930.352 |
| 37 | 24.157.817 |
| 38 | 39.088.169 |
| 39 | 63.245.986 |
| 40 | 102.334.155 |
| 41 | 165.580.141 |
| 42 | 267.914.296 |
| 43 | 433.494.437 |
| 44 | 701.408.733 |
| 45 | 1.134.903.170 |
| 46 | 1.836.311.903 |
| 47 | 2.971.215.073 |
| 48 | 4.807.526.976 |
| 49 | 7.778.742.049 |
| 50 | 12.586.269.025 |
| 51 | 20.365.011.074 |
| 52 | 32.951.280.099 |
| 53 | 53.316.291.173 |
| 54 | 86.267.571.272 |
| www.osfantasticosnumerosprimos.com.br | |
Esta propriedade foi descoberta pelo matemático Charles Raine. [1]
Escolhe-se 4 termos consecutivos da Sequência de Fibonacci:
Produtos dos extremos
1 x 3 = 3
O dobro do produto dos meios
2 x 1 x 2 = 4
Soma do quadrados dos meios
12 + 22 = 1 + 4 = 5
Terno pitagórico com Números de Fibonacci: 3, 4 e 5
Observação:
5 é o quinto número de Fibonacci.
5 é a medida da hipotenusa.
5 é um número primo.
Produto dos extremos
1 x 5 = 5
O dobro do produto dos meios
2 x 2 x 3 = 12
Soma do quadrados dos meios
22 + 32 = 4 + 9 = 13
Terno pitagórico com Números de Fibonacci: 5, 12 e 13
Observação:
13 é o sétimo número de Fibonacci.
13 é a medida da hipotenusa.
13 é um número primo.
Produto dos extremos
2 x 8 = 16
O dobro do produto dos meios
2 x 3 x 5 = 30
Soma do quadrados dos meios
32 + 52 = 9 + 25 = 34
Terno pitagórico derivado com Números de Fibonacci: 16, 30 e 34
Observação:
34 é o nono número de Fibonacci.
34 é a medida da hipotenusa.
Produto dos extremos
3 x 13 = 39
O dobro do produto dos meios
2 x 5 x 8 = 80
Soma do quadrados dos meios
52 + 82 = 25 + 64 = 89
Terno pitagórico com Números de Fibonacci: 39, 80 e 89
Observação:
89 é o décimo primeiro número de Fibonacci.
89 é a medida da hipotenusa.
89 é primo.
Produto dos extremos
5 x 21 = 105
O dobro do produto dos meios
2 x 8 x 13 = 204
Soma do quadrados dos meios
82 + 132 = 64 + 169 = 233
Terno pitagórico com Números de Fibonacci: 105, 204 e 233
Observação:
233 é o décimo terceiro número de Fibonacci.
233 é a medida da hipotenusa.
233 é primo.
Produto dos extremos
8 x 34 = 272
O dobro do produto dos meios
2 x 13 x 21 = 546
Soma do quadrados dos meios
132 + 212 = 169 + 441 = 610
Terno pitagórico com Números de Fibonacci: 272, 546 e 610
Observação:
610 é o décimo quinto número de Fibonacci.
610 é a medida da hipotenusa.
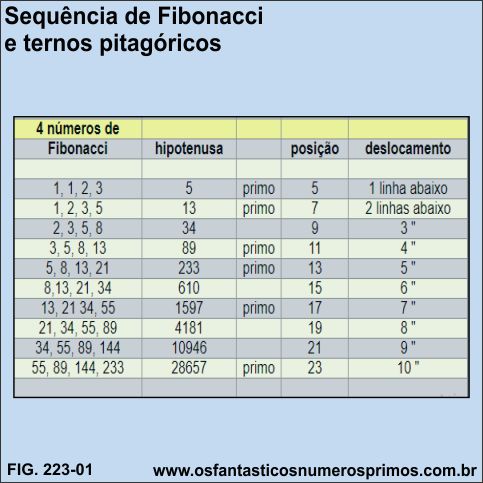
A partir de quatro números consecutivos da Sequência de Fibonacci é possível formar terno pitagórico.
Os números que se referem à hipotenusa em um triângulo retângulo escaleno são números que estão em posições ímpares na Sequência de Fibonacci e entre eles números primos.
A soma dos quadrados de dois termos centrais de cada sequência tem como resultado um número de Fibonacci (hipotenusa).
A posição entre o último termo de cada sequência de 4 números e o resultado da soma dos quadrados de dois termos centrais (hipotenusa) segue um deslocamento natural.
Interessante observar que nos estudos publicados no Livro Ternos Pitagóricos e Sequências Numéricas, em um rol com mais de 200.000 números naturais, encontrou-se apenas 5 ternos pitagóricos primitivos utilizando progressão aritmética (sequência em que são gerados números a partir do número 1, somado-se sempre o número 1). As Fórmulas de Euclides geram ternos pitagóricos primitivos sequencialmente, mas não ternos pitagóricos derivados. [2]
| Sequência de Fibonacci | ||||
|---|---|---|---|---|
| e | ||||
| Ternos Pitagóricos | ||||
| 4 números de | ||||
| Fibonacci | hipotenusa | posição | deslocamento | |
| 1, 1, 2, 3 | 5 | primo | 5 | 1 linha abaixo |
| 1, 2, 3, 5 | 13 | primo | 7 | 2 linhas abaixo |
| 2, 3, 5, 8 | 34 | 9 | 3 " | |
| 3, 5, 8, 13 | 89 | primo | 11 | 4 " |
| 5, 8, 13, 21 | 233 | primo | 13 | 5 " |
| 8,13, 21, 34 | 610 | 15 | 6 " | |
| 13, 21 34, 55 | 1597 | primo | 17 | 7 " |
| 21, 34, 55, 89 | 4181 | 19 | 8 " | |
| 34, 55, 89, 144 | 10946 | 21 | 9 " | |
| 55, 89, 144, 233 | 28657 | primo | 23 | 10 " |
| www.osfantasticosnumerosprimos.com.br | ||||
Autor: Ricardo Silva - julho/2019
[1] FERREIRA, Rogério Augusto. Sequência de Fibonacci - Trabalho apresentado à disciplina de Pesquisa em Matemática II, do Curso de Matemática Bacharelado e Licenciatura do Centro UNIFIEO, 2007
[2] SILVA, Ricardo José. Ternos Pitagóricos e sequências numéricas - livro digital, São Paulo, 2017.
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato