


François-Édouard-Anatole Lucas (1842-1891), matemático francês e estudioso das obras de Leonardo de Pisa foi quem popularizou os Números de Fibonacci em sua obra Recherches Sur Plusierurs Ouvrages de Léonard de Pisa (1877) e que através dela criou outra sequência semelhante chamada de Sequência de Lucas: 2, 1, 3, 4, 7, 11, 18,...
Foi um dos precursores da Matemática Recreativa com a publicação da obra Récréations mathématiques (4 Bände), Gauthier-Villars, Paris, 1882–1894 e também criador do Jogo Torre de Hanoi.
Outro feito, foi ter descoberto o 120 número primo de Mersenne com 39 dígitos:
M127 = 2127-1
= 17.141.183.
e que permanece como recorde (75 anos) tal descoberta sem uso de computador.[2]
A Sequência de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,... é formada com a repetição do número 1 duas vezes e a partir do terceiro termo soma-se com o antecessor, ela apareceu em um problema em que se desejava saber o crescimento de população de coelhos e foi publicada no livro Liber Abacci - Livro do Ábaco ou do Cálculo - (1202) de autoria de Leonardo de Pisa (1175-?), conhecido como Fibonacci.
Terno Pitagórico é uma sequência de três números inteiros que satisfazem ao Teorema de Pitágoras, onde: (a2 = b2 + c2) - O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
a = m2 -n2
b = 2mn
c = m2+n2
onde:
m > n (m tem que ser maior que n)
m e n (tem que ser primos entre si, into é, o mdc é igual a 1)
Observação: dois números consecutivos são primos entre si.
Exemplo 1)
2 e 1
a = 22 - 12 = 4 - 1 = 3
b = 2 . 2 . 1 = 4 . 1 = 4
c = 22 + 12 = 4 + 1 = 5
3, 4 e 5 é um Terno Pitagórico Primitivo.
Exemplo 2)
3 e 2
a = 32 - 22 = 9 - 4 = 5
b = 2 . 3 . 2 = 6 . 2 = 12
c = 32 + 22 = 9 + 4 = 13
5, 12 e 13 é um Terno Pitagórico Primitivo.
Primeiros 54 termos da Sequência de Lucas.
| Sequência de Lucas | |
|---|---|
| posição/ordem | números de Lucas |
| 1 | 2 |
| 2 | 1 |
| 3 | 3 |
| 4 | 4 |
| 5 | 7 |
| 6 | 11 |
| 7 | 18 |
| 8 | 29 |
| 9 | 47 |
| 10 | 76 |
| 11 | 123 |
| 12 | 199 |
| 13 | 322 |
| 14 | 521 |
| 15 | 843 |
| 16 | 1.364 |
| 17 | 2.207 |
| 18 | 3.571 |
| 19 | 5.778 |
| 20 | 9.349 |
| 21 | 15.127 |
| 22 | 24.476 |
| 23 | 39.603 |
| 24 | 64.079 |
| 25 | 103.682 |
| 26 | 167.761 |
| 27 | 271.443 |
| 28 | 439.204 |
| 29 | 710.647 |
| 30 | 1.149.851 |
| 31 | 1.860.498 |
| 32 | 3.010.349 |
| 33 | 4.870.847 |
| 34 | 7.881.196 |
| 35 | 12.752.043 |
| 36 | 20.633.239 |
| 37 | 33.385.282 |
| 38 | 54.018.521 |
| 39 | 87.403.803 |
| 40 | 141.422.324 |
| 41 | 228.826.127 |
| 42 | 370.248.451 |
| 43 | 599.074.578 |
| 44 | 969.323.029 |
| 45 | 156.839.7607 |
| 46 | 2.537.720.636 |
| 47 | 4.106.118.243 |
| 48 | 6.643.838.879 |
| 49 | 10.749.957.122 |
| 50 | 17.393.796.001 |
| 51 | 28.143.753.123 |
| 52 | 45.537.549.124 |
| 53 | 73.681.302.247 |
| 54 | 11.921.885.1371 |
| www.osfantasticosnumerosprimos.com.br | |
Eis algumas relações numéricas, dentre outras, entre Números de Lucas e Números de Fibonacci.
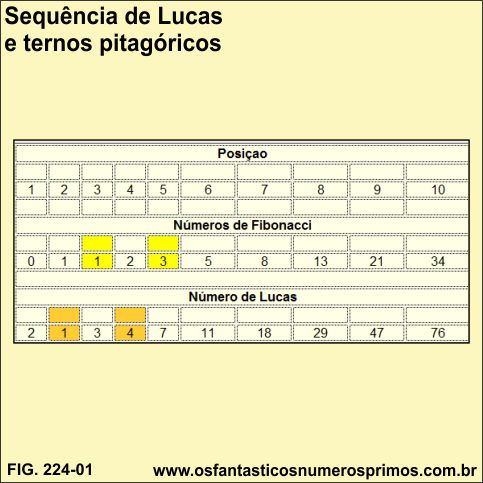
Escolhendo-se 3 termos de Fibonacci e somando-se os extremos, tem-se como resultado um número de Lucas.
Exemplos:
0 + 1 = 1
1 + 2 = 3
1 + 3 = 4
| Posiçao | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Números de Fibonacci | |||||||||
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
| Número de Lucas | |||||||||
| 2 | 1 | 3 | 4 | 7 | 11 | 18 | 29 | 47 | 76 |
Escolhendo-se 3 termos de Lucas e somando-se o extremos, tem-se como resultado um múltiplo de 5 e consequentemente número divisor de Lucas.
Exemplos:
2 + 3 = 5 (divisor de 1 e 5 )
1 + 4 = 5 (divisor de 1 e de 5)
3 + 7 = 10 (divisor de 2 e de 5)
4 + 11 = 15 (divisor de 3 e de 5)
7 + 18 = 25 (divsor de 5)
Esta propriedade foi descoberta pelo matemático Charles Raine, a qual foi utilizada para encontrar ternos pitagóricos na Sequência de Fibonacci (ver matérias relacionadas). [1]
Baseia-se no mesmo princípio, escolhe-se 4 termos consecutivos, neste caso, da Sequência de Lucas e executam-se as seguintes etapas:
Produto dos extremos
2 x 4 = 8
O dobro do produto dos meios
2 x 1 x 3 = 6
Soma do quadrados dos meios
12 + 32 = 1 + 9 = 10
Terno pitagórico derivado: 8, 6 e 10.
Produto dos extremos
1 x 7 = 7
O dobro do produto dos meios
2 x 3 x 4 = 24
Soma do quadrados dos meios
32 + 42 = 9 + 16 = 25
Terno pitagórico primitivo: 7, 24 e 25.
Produto dos extremos
3 x 11 = 33
O dobro do produto dos meios
2 x 4 x 7 = 56
Soma do quadrados dos meios
42 + 72 = 16 + 49 = 65
Terno pitagórico primitivo: 33, 56 e 65
Produto dos extremos
4 x 18 = 72
O dobro do produto dos meios
2 x 7 x 11 = 154
Soma do quadrados dos meios
72 + 112 = 49 + 121 = 170
Terno pitagórico derivado: 72, 154 e 170
Produto dos extremos
7 x 29 = 203
O dobro do produto dos meios
2 x 11 x 18 = 396
Soma do quadrados dos meios
112 + 182 = 121 + 324 = 445
Terno pitagórico primitivo: 203, 396 e 445.
A partir de quatro números consecutivos da Sequência de Lucas é possível formar terno pitagórico.
Diferentemente dos ternos pitagóricos gerados por números de Fibonacci em que nos ternos pitagóricos aparecem números de Fibonacci sequencialmente, nos ternos pitagóricos gerados por números de Lucas não há esta regularidade.
Interessante observar que nos estudos publicados no Livro Ternos Pitagóricos e Sequências Numéricas, em um rol com mais de 200.000 números naturais, encontrou-se somente 5 ternos pitagóricos primitivos utilizando progressão aritmética (sequência em que são gerados números a partir do número 1, somado-se sempre o número 1). As Fórmulas de Euclides geram ternos pitagóricos primitivos sequencialmente, mas não ternos pitagóricos derivados [3]
Aqui nos exemplos expostos, em um rol com 54 termos, da Sequência de Lucas em que os números são gerados sempre somando dois números anteriores, foram gerados 5 ternos pitagóricos sequenciais.
A Sequência de Lucas não é um progressão aritmética e nem geométrica e mesmo assim possui diversas propriedades numéricas e matemáticas.
Autor: Ricardo Silva - julho/2019
[1] FERREIRA, Rogério Augusto. Sequência de Fibonacci - Trabalho apresentado à disciplina de Pesquisa em Matemática II, do Curso de Matemática Bacharelado e Licenciatura do Centro UNIFIEO, 2007
[2] ASTROLINO e SILVA, Bruno. Números de Fibonacci e números de Lucas. Dissertação (Mestrado de Pós Graduação em Mestrado Profissional em Matemática em Rede Nacional) --Instituto de Ciências Matemáicas e de Computação, Universidade de São Paulo, 2017.
[3] SILVA, Ricardo José. Ternos Pitagóricos e sequências numéricas - livro digital, São Paulo, 2017.
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato