


A Sequência de Fibonacci é formada repetindo-se o número 1 duas vezes e partir do terceiro termo somando-se o termo anterior:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987...
...é uma sequência originada de um problema no qual a partir de um casal de coelhos, depois de 12 meses, quantos coelhos existirão no total, não considerando situações adversas como mortes, doenças, etc..., publicada no livro Liber Abaci (Livro de Cálculos) no ano de 1202.
Johannes Kepler, astronômo, astrólogo e matemático alemão, no ano de 1611, percebe que dividindo um termo posterior com um termo anterior apresenta como resultado o número 1,6180339887
| Sequência de Fibonacci | Número de Ouro |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 2 | 1,5 |
| 3 | 1,666666667 |
| 5 | 1,604984472 |
| 8 | 1,618033989 |
| 13 | 1,618033989 |
| 21 | 1,618033989 |
| 34 | 1,618033989 |
| 55 | 1,618033989 |
| 89 | 1,618033989 |
| 144 | 1,618033989 |
| 233 | 1,618033989 |
| 377 | 1,618033989 |
| 610 | 1,618033657 |
François-Édouard-Anatole Lucas (1842-1891), matemático francês, foi quem notou pela primeira vez que nos números dos problemas dos coelhos a partir do terceiro termo, somando-se um termo anterior, obtem-se o próximo termo.
A partir desta observação, François-Édouard-Anatole Lucas e outros mátemáticos posteriores descobriram outras diversas propriedades relacionadas à Sequência de Fibonacci como:
Sequência de Lucas - originada dos números de Fibonacci;
Definição recursiva;
Propriedades da soma entre termos da sequência de Fibonacci;
Produto dos termos da sequência de Fibonacci;
Fórmula de Binet;
Razão Áurea, etc.
Os números de Fibonacci aparecem na fauna, flora, geometria, arquitetura, fenômenos físicos, etc...
O matemático Charles W. Raine descobriu que escolhendo-se 4 termos consecutivos da Sequência de Fibonacci são possíveis de se formarem Ternos Pitagóricos.
Ternos Pitagóricos são sequências de três números inteiros que satisfazem ao Teorema de Pitágoras com os quais são possíveis de se construirem triângulos retângulos escalenos, também chamados de Triângulos Retângulos Pitagóricos.
Produtos dos extremos
1 x 3 = 3
O dobro do produto dos meios
2 x 1 x 2 = 4
Soma do quadrados dos meios
12 + 22 = 1 + 4 = 5
Terno pitagórico formados com Números de Fibonacci: 3, 4 e 5.
A geração de Ternos Pitagóricos não estão restrito a Sequência de Fibonacci, mas partindo-se do Método de Fibonacci outras sequências numéricas podem ser formadas e aplicar o Método de Charles W. Raine para se gerarem Ternos Pitagóricos.
Números escolhidos: 1 e 3
1, 3, 4, 7
Produtos dos extremos
1 x 7 = 7
O dobro do produto dos meios
2 x 3 x 4 = 24
Soma do quadrados dos meios
32 + 42 = 9 + 16 = 25
Terno pitagórico formado: 7, 24 e 25.
Este método aparece no WebSite:
https://
do Dr. Ron Knott o qual foi extraído de: Pythagorean triangles from the Fibonacci Series C W Raine Scripta Mathematica vol 14 (1948) page 164
Escolhendo-se dois termos consecutivos da Sequência de Fibonacci e aplicando o Teorema de Pitágoras, o resultado da hipotenusa é um radical cujo radicando é um número de Fibonacci.
Exemplo:
Números escolhidos 1 e 2.
O número 1, que é o primeiro termo, é o denominado de cateto menor.
O número 2, que é o segundo termo, é o denominado de cateto maior.
Aplicando o Teorema de Pitágoras, a hipotenusa tem como resultado o radical √5 cujo radicando é um número de Fibonacci.
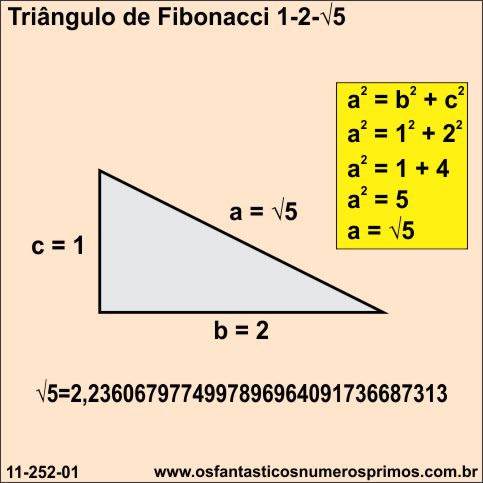
A presente tabela lista os 23 primeiros números de Fibonacci, formando duplas de números consecutivos (cateto menor e cateto maior) relacionados aos lados de um triângulo retângulo.
Assim como a razão entre um número de Fibonacci e o seu antecessor tem como resultado o Número de Ouro (Phi), a razão entre uma hipotenusa e uma hipotenusa anterior também é um número (Phi).
Importante destacar que:
a) os radicais referente as hipotenusas não são consecutivos, por exemplo entre os radicais √2 e √5, há um intervalo de dois radicais "faltantes";
b) os radicandos são números de Fibonacci.
| Triângulo de Fibonacci | ||||
|---|---|---|---|---|
| regularidades na hipotenusa | ||||
| cateto | cateto | hipotenusa | raiz | phi |
| menor | maior | quadrada | ||
| (c) | (b) | (a) | ||
| 1 | 1 | √2 | 1,414 | 1,581 |
| 1 | 2 | √5 | 2,236 | 1,612 |
| 2 | 3 | √13 | 3,605 | 1,617 |
| 3 | 5 | √34 | 5,830 | 1,617 |
| 5 | 8 | √89 | 9,433 | 1,618 |
| 8 | 13 | √233 | 15,264 | 1,618 |
| 13 | 21 | √610 | 24,698 | 1,618 |
| 21 | 34 | √1.597 | 39,962 | 1,618 |
| 34 | 55 | √4.181 | 64,660 | 1,618 |
| 55 | 89 | √10.946 | 104,623 | 1,618 |
| 89 | 144 | √28.657 | 169,283 | 1,618 |
| 144 | 233 | √75.025 | 273,906 | 1,618 |
| 233 | 377 | √196.418 | 443,190 | 1,618 |
| 377 | 610 | √514.229 | 717,097 | 1,618 |
| 610 | 987 | √1.346.269 | 1160,288 | 1,618 |
| 987 | 1.597 | √3.524.578 | 1877,385 | 1,618 |
| 1.597 | 2.584 | √9.227.465 | 3037,674 | 1,618 |
| 2.584 | 4.181 | √24.157.817 | 4915,060 | 1,618 |
| 4.181 | 6.765 | √63.245.986 | 7952,734 | 1,618 |
| 6.765 | 10.946 | √165.580.141 | 12867,794 | 1,618 |
| 10.946 | 17.711 | √433.494.437 | 20820,529 | 1,618 |
| 17.711 | 28.657 | √1.134.903.170 | 33688,323 | 1,618 |
| 28.657 | 46.368 | √2.971.215.073 | 54508,853 | 1,618 |
Aplicando as relações trigonométricas a cada triângulo retângulo formado pelas duplas de números consecutivos da Sequência de Fibonacci da tabela acima que formam os catetos e com o resultado da hipotenusa, os valores de seno, cosseno e tangente apresentam-se constantes.
Interessante observar que a tangente é 0,618
| Triangulo de Fibonacci | ||
|---|---|---|
| relações trigonométricas | ||
| seno | cosseno | tangente |
| 0,511667274 | 0,82789504 | 0,618033989 |
| 0,523606798 | 0,847213595 | 0,618033989 |
| 0,525419567 | 0,850146718 | 0,618033989 |
| 0,525685624 | 0,850577207 | 0,618033989 |
| 0,525724475 | 0,850640069 | 0,618033989 |
| 0,525730144 | 0,850649241 | 0,618033989 |
| 0,525730971 | 0,85065058 | 0,618033989 |
| 0,525731092 | 0,850650775 | 0,618033989 |
| 0,525731109 | 0,850650803 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
| 0,525731112 | 0,850650808 | 0,618033989 |
a) A partir de dois números escolhidos que formam os catetos, os intervalos até a hipotenusa formam uma progressão aritmética de razão 1: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10...}
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
0 intervalo
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
1 intervalo
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
2 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
3 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
4 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
5 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
6 intervalos
b) A partir do primeiro termo da Sequência de Fibonacci até os dois números escolhidos que formam os catetos, os intervalos formam uma progressão aritmética de razão 1 a partir da segunda linha: { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10...}
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
0 intervalo
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
1 intervalo
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
2 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
3 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
4 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
5 intervalos
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 |
Autor: Ricardo Silva - abril /2020
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018>
SILVA, Ricardo José da. Sequência Numéricas Mágicas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014
https://
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

NOVO LIVRO DIGITAL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato