


Certa cidade A, querendo incentivar a ida de famílias para aumentar sua população, institui um concurso público de doações de terrenos para que famílias construam casas.
Na prova do concurso público, todos os membros de cada família devem participar e esta ganhando terá o direito de demarcar livremente a área de terreno que futuramente será construída a casa onde residirão.
O concurso público consiste das seguintes etapas:
1) exame teórico para todos os membros de cada família;
2) sendo a família aprovada no exame teórico passa para a etapa seguinte para demarcar a área do terreno:
3) escolhe-se um membro da famíla, por exemplo, o pai para demarcar o terreno;
4) a pessoa escolhida deverá ficar com os olhos totalmente vendados, isto é, cobertos com um tipo de tapa-olhos;
5) a pessoa escolhida receberá 4 marcadores, tipo estaca, cones, tijolos, etc;
6) a pessoa escolhida terá o tempo de 80 segundos para demarcar os quatro pontos para formar a figura aproximada de um retangulo do futuro terreno;
7) a pessoa, então, deverá andar normalmente e os passos de sua caminhada será convertido em metros e desta forma determinar o perímetro do terreno.
Elaborando-se um modelo matemático, poderiámos ter os passos de determinada pessoa conforme o exemplo a seguir formando um retângulo.
Com passos convertidos em metros, o terreno poderia ter, por exemplo, um perímetro de 30 metros e uma área de 50m2.
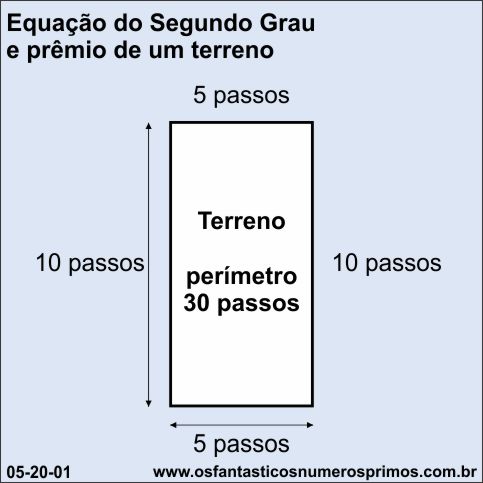
Um prefeito da cidade B também resolve fazer um concurso público semelhante, sabendo que os participantes conseguiram demarcar terrenos de aproximadamente 50 metros quadrados (50m2), ele oferecerá terrenos de 75 metros quadrados (75m2).

A prova do concurso público consiste na resolução de uma Equação do Segundo Grau com o Método de Completar Quadrados.
Cada um dos membros de cada família participante deverá resolver a equação e explicar o Método de Completar Quadrados.
x2 + 10x = 75
i)
Equação do Segundo Grau completa na forma:
ax2 + bx - c = 0
ii)
x2 + 10x = 75
x2 + 10x - 75 = 0
iii)
| x2 | + | 10 x | - | 75 | = | 0 |
Passe o termo "c" para o primeiro membro e troque o sinal para positivo.
Divida o coeficiente 10 do termo "bx" por 2, (faça a divisão mentalmente) o quociente é 5.
| 10 x | ||||
| x2 | + | ___ | = | 75 |
| 2 |
iv)
Eleve quociente 5 ao quadrado (o resultado é 25) e some ao primeiro membro.
| x2 | + | 10 x | + | 25 | = | 75 |
v)
Some também o quadrado 25 ao segundo membro para equilibrar a equação.
| x2 | + | 10 x | + | 25 | = | 75 | + | 25 |
vi)
Efetue a adição no segundo membro.
No primeiro membro tem-se um trinômio quadrado perfeito.
| x2 | + | 10 x | + | 25 | = | 100 |
vii)
Fatore o trinômio quadrado perfeito no primeiro membro, obtendo um quadrado da soma (produto notável).
| ( x + 5 )2 | = | 100 |
viii)
Extraia a raiz quadrada dos dois membros.
| ( x + 5 ) | = | ± √100 |
ix)
| x + 5 | = | ± 10 |
x)
Solução Positiva
| x' | = | + 10 - 5 |
| x' | = | + 5 |
xi)
Solução Negativa
| x' | = | - 10 - 5 |
| x' | = | - 15 |
O prefeito da cidade C também resolve doar terrenos, com área de 85 metros quadrados (85m2) e a condição é resolver a equação da cidade B por meio da Fórmula de Bháskara por cada membro de cada família no tempo de 10 minutos cada um.
| - b ± √b 2 - 4 . a .c | ||
| x | = | _____________ |
| 2.a |
| Δ = b2 - 4 . a . c |
i)
Monta-se a Equação do Segundo Grau x2 + 10x = 75 na forma ax2 + bx + c = 0.
| x 2 + 10 x -75 | = | 0 |
ii)
Aplicando e resolvendo o Delta (Discriminante da equação).
| Δ = 10 2 - 4 . 1 ( - 75) |
iii)
| Δ = 100 + 300 |
iv)
O Delta é maior que 0, portanto, há duas raízes
| Δ = 400 |
v)
Extraindo a raiz quadrada.
| - b ± √Δ | ||
| x | = | _________ |
| 2 . 1 |
| -10 ± √400 | ||
| x | = | _________ |
| 2 .1 |
| -10 ± 20 | ||
| x | = | ______ |
| 2 |
vi)
Solução negativa.
| - 10 - 20 | ||
| x' | = | _______ |
| 2 |
| - 30 | ||||
| x' | = | ___ | = | - 15 |
| 2 |
vii)
Solução positiva.
| - 10 + 20 | ||
| x'' | = | _______ |
| 2 |
| + 10 | ||||
| x'' | = | ____ | = | 5 |
| 2 |
Um outro prefeito, da cidade D também resolve doar terrenos, com área de 85 metros quadrados (85m2) e a condição é resolver a equação da cidade C por meio da meio Soma e Produto das Raízes por cada membro de cada família no tempo de 4 minutos cada um.
Monta-se a Equação do Segundo Grau x2 + 10x = 75 na forma ax2 + bx + c = 0.
i)
| x 2 + 10 x - 75 | = | 0 |
ii)
as relações entre coeficientes e raízes da Equação do Segundo Grau se baseiam nas seguinte fórmulas:
a SOMA das raízes é igual ao quociente do oposto de b por a:
| - b | ||||
| S | = | x' + x'' | = | ___ |
| a |
o PRODUTO das raízes é igual ao quociente de c por a:
| c | ||||
| P | = | x' . x'' | = | ___ |
| a |
iii)
no Método da Soma e Produto, o ideal é começar por descobrir dois números cujo o PRODUTO é 75.
a dica é fazer multiplicações para descobrir fatores do produto 75:
1 x 75 = 75
3 x 25 = 75
5 x 15 = 75
| 15 | x | 5 | = | 75 |
iv)
encontrando dois números cuja a soma é 10 (positivo).
+ 15 - 5 = 10
| 15 | + | (- 5 ) | = | 10 |
As raízes da equação são 5 e 15.
Autor: Ricardo Silva- maio/2020
ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato