


Pense em dois números inteiros, por exemplo, o número 4 e o número 12.
Por meio da Adição pode-se obter o número 4 através de duas expressões numéricas.
1 + 3 = 4
2 + 2 = 4
Por meio da Multiplicação pode-se obter o número 12 através de três expressões numéricas.
1 x 3 = 12
2 x 6 = 12
3 x 4 = 12
Agora você tem o seguinte problema matemático para resolver, uma Equação do Segundo Grau do tipo x2 + bx = c
x2 + 4x = 12
Para resolve-la, pode-se utilizar o Método de Completar Quadrados com a Álgebra e a Geometria.
onde o termo x2 está representando um quadrado e
o termo 4x está representando um retângulo.
Quer-se saber quais são as raízes da soma de um quadrado com 4 vezes o seu lado cujo resultado é 12.
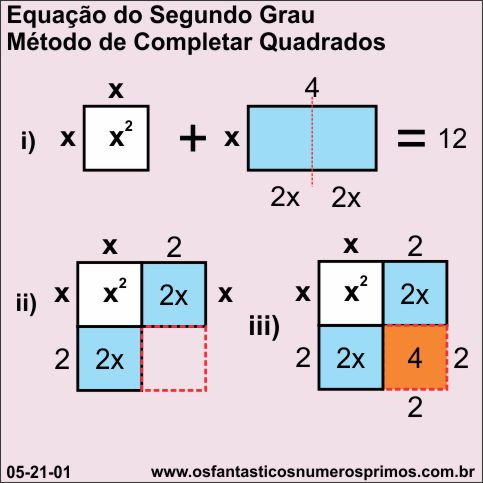
Precisa-se descobrir quais são os números cuja soma é 4 e o produto é 12.
i)
monta-se a equação.
x2 + 4x = 12
divide-se o retângulo (azul) 4x em duas partes, 2x e 2x e...
ii)
...coloca-se um ao lado do quadrado x2 e outro abaixo.
x2 + 2x + 2x = 12
veja que fica sobrando uma área que deverá ser completada.
iii)
multiplica-se os quadrados (azul) de lado 2, obtendo-se a área de 4 unidades a ser completada.
acrescenta 4 aos dois membros da equação.
x2 + 2x + 2x + 4 = 12 + 4
reduz-se os termos semelhantes
x2 + 4x + 4 = 12 + 4
o primeiro membro torna-se um trinômio quadrado perfeito e...
x2 + 4x + 4 = 16
devemos fatorá-lo em um quadrado da soma de dois termos (Produto Notável).
(x+ 2)2 = 16
extraí-se a raiz quadrada nos dois lados da equação.
x + 2 = ± √16
x + 2 = ± 4
Solução positiva
x' = + 4 - 2 = 2
Solução negativa
x'' = - 4 - 2 = -6
Autor: Ricardo Silva - maio/2020
ANDRADE, Bernardino Carneiro de . A evolução histórica da resolução das equações do 2o grau. Departamento de Matemática Pura da Faculdade de Ciências da Universidade do Porto,2000
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato