


Você deseja saber a raiz quadrada de 2 (√2), tendo a disposição nos dias atuais, fabulosos dispositivos eletrônicos digitais, então você pode se dar o luxo de poder escolher, por exemplo, calculadora, tablet, computador ou principalmente telefone celular.
Tecla 2 e o símbolo da √ e os cálculos, num piscar de olhos, podem ser apresentados, conforme o dispositivo, da seguinte forma:
Calculadora de bolso
1,4142135... (7 casas decimais após a vírgula);
Calculadora científica de bolso
1,41421352... (9 casas decimais após a vírgula);
Calculadora padrão do Sistema Windows
1,414213562373095... (15 casas decimais após a vírgula);
Calculadora científica do Sistema Windows
1,414213562373095048
Voltando no tempo, na região da Mesopotâmia, pesquisadores encontraram tabletes de barro com escrita cuneiforme da civilização babilônica em que as incrições indicam cálculos realizados em figura de um quadrado, demonstrando a extração da raiz quadrada de 2 aproximada 1,414212962..., com datação entre 1.800 a 1.600 a.C.

Em outro tablete, denominado de Pimpliton 322, datado de aproximadamente 1.800 a.C, há uma tabela com ternos pitagóricos.

Multiplicando-se um número inteiro por ele mesmo ou elevando à potência 2, obtem-se um número quadrado perfeito:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 12 | ? | ? | 22 | ? | ? | ? | ? | 32 |
exemplo 1)
1 x 1 = 1
Extraindo-se a raiz quadrada de 1, obtem-se o número inteiro 1.
√1 = 1
exemplo 2)
2 x 2 = 4
Extraindo-se a raiz quadrada de 4, obtem-se o número inteiro 2.
√4 = 2
exemplo 2)
3 x 3 = 9
Extraindo-se a raiz quadrada de 9, obtem-se o número inteiro 3.
√9 = 3
Qual é o número que multiplicado por ele mesmo tem como resultado o número 2 ?
? x ? = 2
E qual é a sua raiz quadrada?
√2 = ?
Qual é o número que multiplicado por ele mesmo tem como resultado o número 3 ?
? x ? = 3
E qual é a sua raiz quadrada?
√3 = ?
O número 2 se encontra entre os números quadrados 1 e 4 e para obter a sua raiz quadrada, um dos métodos é efetuar os cálculos numéricos com aproximações sucessivas através de representação decimal.
| 1 | 2 | 3 | 4 |
| 12 | ? | ? | 22 |
1,2 2 = 1,44
1,3 2 = 1,69
1,4 2 = 1,96
1,41 2 = 1,9881
1,413 2 = 1,996569
1,414 2 =1,999396
1,4142 2 =1,99996164
Se continuarmos os cálculos, a representação decimal, continuará sendo não exata e não periódica, isto é, a parte decimal apresentará números aleatórios, sem um padrão numérico.
Portanto, a sequência numérica {√2, √3, √5, √6, √7, √8...} é composta por números irracionais.
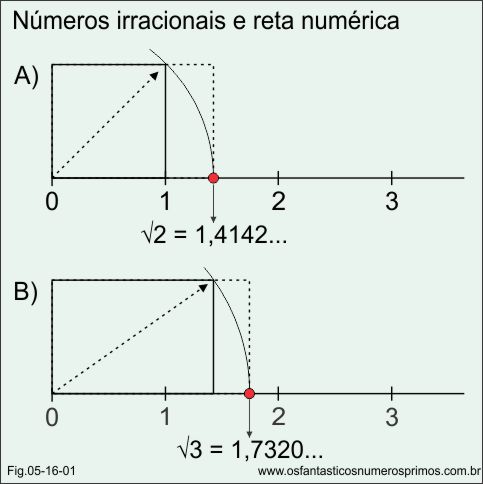
Números irracionais podem ser obtidos por meio de reta numérica, da seguinte forma:
Detalhe A)
a) constrói-se uma reta numérica;
b) desenha-se um quadrado de lado 1;
c) centro no ponto 0, traça-se um arco do vértice superior direito até a reta numérica;
d) na intersecção do arco com a reta numérica se encontra a √2.
e) prolongrando-se a lateral direta do quadrado, forma-se um retângulo de raiz 2.
Detalhe B)
f) a partir do retângulo de raiz 2;
g) centro no ponto 0, traça-se um arco do vértice superior direito até a reta numérica;
h) na intersecção do arco com a reta numérica se encontra a √3.
i) prolongrando-se a lateral direta do retângulo de raiz 2, forma-se um retângulo de raiz 3.
Continuando-se este processo, obtem-se os demais números irracionais.
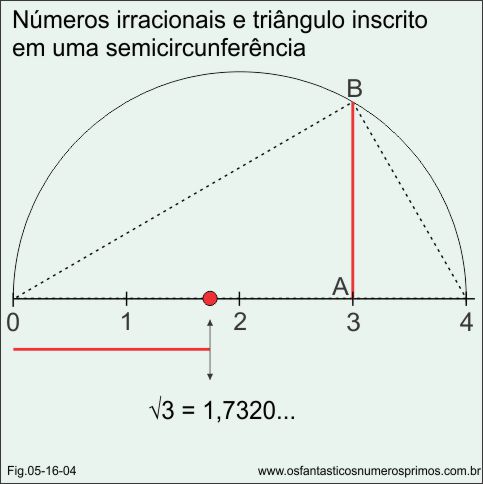
Números irracionais podem ser obtidos por meio de triângulo inscrito em uma semicircunferência.
Para se saber, por exemplo, a raiz quadrada de 3 (√3) através de triângulo inscrito em uma semicircunferência, procedemos da seguinte forma:
a) 3 x 1 = 3;
b) soma-se 3 + 1 = 4;
c) constrói-se uma reta numérica com 4 unidades;
d) determina-se o ponto médio e traca-se uma semicircunferência;
e) 3 unidades determinam a projeção do cateto maior e 1 unidade cateto menor;
f) no ponto 3 do diâmetro (reta numerada), traça-se a altura AB do triângulo inscrito;
g) efetuam-se os cálculos:
(AB) 2 = 3 x 1
(AB) 2 = 3
AB = √3
h) transportando o seguimento AB para reta numerada (diâmetro), obtem-se o ponto correspondente a √3.
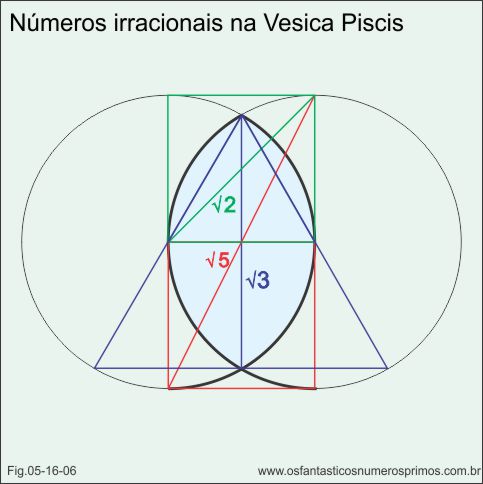
A Vesica Piscis é uma construção geométrica com duas circunferências de mesmo raio na qual o centro de uma se encontra na circunferência da outra.
Com ela é possivel construir diversos desenhos simbólicos, polígonos de n lados de mesmo comprimento e inúmeras construções geométricas complexas.
Em uma de suas construções mais simples, é possível encontrar as raízes: √2, √3 e √5, inscrevendo quadrados e triângulos equiláteros, conforme demonstração geométrica da (fig.05-16-06).
Segundo Robert Lawlor, autor de A Geometria Sagrada:
"O aspecto das três raízes sagradas pode se resumir neste simples diagrama. Estas três relações-raízes são tudo o que é necessário para a formação dos cinco sólidos regulares ("platônicos") que são a base de todas as formas volumétricas. Também o 2, o 3 e o 5 são os únicos números necessários para a divisão da oitava em escalas musicais. Podemos aceitar, portanto, estas raízes como uma trindade de princípios geradores."
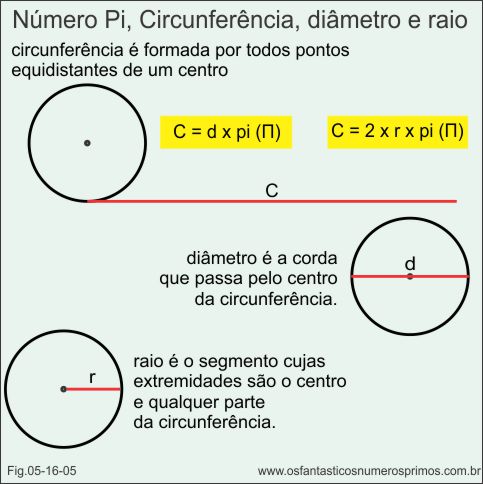
O número pi (Π) é a relação entre a medida do comprimento de uma circunferência com a medida de seu diâmetro e o seu valor é um número decimal, não periódico e infinito 3,1415...
Diferentemente da sequência numérica {√2, √3, √5, √6, √7, √8...}, o número pi é a razão entre dois números, mas nunca dois números inteiros, isto é, quando o diâmetro é um número inteiro; a circunferência é um número decimal não periódico e quando a circunferência é um número inteiro; o diâmetro é um número decimal não periódico.
Exemplo 1)
Comprimento da circunferência:
C = ?
Diâmetro da circunferência:
d = 10
Cálculo:
10 x (Π) = 3,141592653589793
Exemplo 2)
Comprimento da circunferência:
C = 10
Diâmetro da circunferência:
d = ?
Cálculo:
10 : (Π) = 3,183098861837906
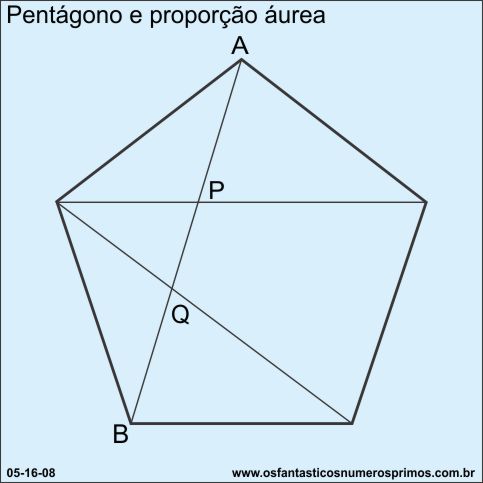
Sengundo H. E. Huntley, os pitagóricos tinham predileção pelo pentágono, pois a partir de sua forma obtinham a figura do pentagrama que adotaram como símbolo da Escola Pitagórica.
Já tinham conhecimento de que diagonais de um pentágono apresentavam proporções áureas.
O ponto P divide AQ e AB internamente e QB externamente em proporção áurea.
Divindindo-se o comprimento da diagonal por um dos lados do pentágono, o resultado é próximo a phi (Ф) - Número de Ouro.
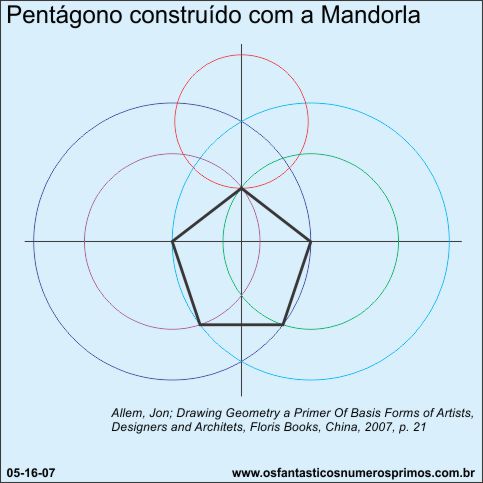
Exemplo de construção de pentágono utilizando como base a Mandorla.
Mandorla e Vesica Piscis são bases com as quais se podem construirem diversas figuras e outras complexas construções geométricas.
Contando as circunferências e os lados do pentágono, 10 etapas para contruí-lo.
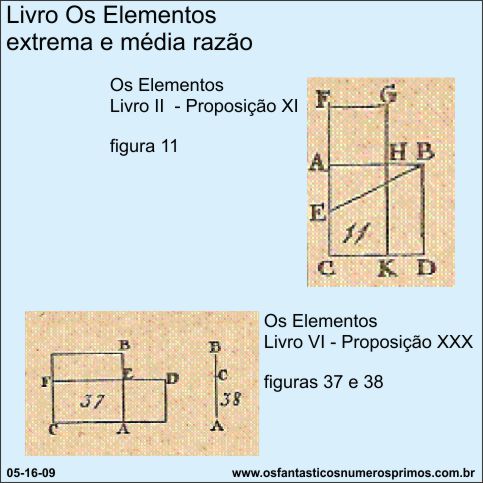
No livro, Os Elementos de Euclides de Alexandria, se encontram as Proposições XI e XXX em que há construções geométricas com estudos sobre extrema e média razão entre segmentos de reta e figuras geométricas.
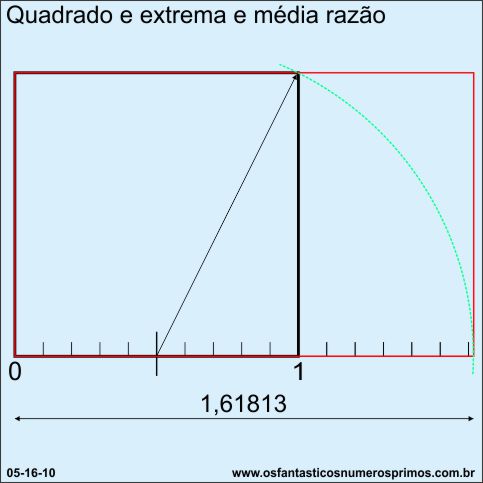
Em uma reta numerada, contruíndo-se um quadrado de lado unitário, com a ponta seca do compasso no ponto médio de sua base, abertura até o vértice direito superior, traçando-se um arco até ao encontro da reta, determina-se um seguimento áureo e consequentemente um retângulo áureo.
A sequência de Fibonacci possui diversas propriedades numéricas e algébricas e entre essas propriedades, uma das mais importantes é o número phi (Ф) - Número de Ouro
O quociente de um número de Fibonacci por um número antecessor gera o número phi (Ф) - Número de Ouro.
| Sequência de Fibonacci | Número de Ouro (Ф) |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 2 | 1,5 |
| 3 | 1,666666667 |
| 5 | 1,604984472 |
| 8 | 1,618033989 |
| 13 | 1,618033989 |
| 21 | 1,618033989 |
| 34 | 1,618033989 |
| 55 | 1,618033989 |
| 89 | 1,618033989 |
| 144 | 1,618033989 |
| 233 | 1,618033989 |
| 377 | 1,618033989 |
| 610 | 1,618033657 |
O obtenção do número phi (Ф) - Número de Ouro, não está restrita à sequência de Fibonacci, mútliplicando-se os números de Fibonnaci por um fator fixo, por exemplo, o número 2, os produtos geram uma nova sequência numérica com a mesma propriedade de se obter o número phi (Ф)
| Múltiplos da | |
|---|---|
| Sequência de Fibonacci | Número de Ouro (Ф) |
| 2 | 1 |
| 2 | 2 |
| 4 | 1,5 |
| 6 | 1,666667 |
| 10 | 1,6 |
| 16 | 1,625 |
| 26 | 1,615385 |
| 42 | 1,619048 |
| 68 | 1,617647 |
| 110 | 1,618182 |
| 178 | 1,617978 |
| 288 | 1,618056 |
| 466 | 1,618026 |
| 754 | 1,618037 |
| 1220 | 1,618033 |
Escolhendo-se dois números aleátorios, por exemplo, 5 e 2 e aplicando o processo da soma de dois números anteriores para se obter o próximo número, a sequência numérica gerada, também apresenta a propriedade de obtenção de números próximo do o número phi (Ф)
| 5 | |
| 2 | 0,4 |
| 7 | 3,5 |
| 9 | 1,285 |
| 16 | 1,777 |
| 25 | 1,562 |
| 41 | 1,64 |
| 66 | 1,609 |
| 107 | 1,621 |
Autor: Ricardo Silva - abril/2020
COMMANDINO, Frederico. Euclides - Elementos de Geometria.
São Paulo: Edições Cultura, 1944.
ISBN - Não indicado.
Fonte: Biblioteca do Clube de Engenharia da Bahia.
Obra digitalizada por: Neuziton Torres Rapadura -
neuzitontr
DANTE, Luiz Roberto . Tudo é Matemática / Luiz Roberto Dante - - 3. ed. - - São Paulo: Àtica, 2009
HUNTLEY, H. E. A divina Proporção. Trad. de Luiz Carlos Ascêncio Nunes. Brasília. Universidade de Brasília., 1985.
LAWLOR, Robert. A Geometria Sagrada. Versão Brasileira: GVS, 1996
NAKAMURA, Keiji. Conjunto do números irracionais: a trajetória de um conteúdo não incorporado às práticas educacionais. Dissertação de Mestrado. Pontifícia Universidade Católica. São Paulo, 2008
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato