


A sequência de Fibonacci é obtida a partir do terceiro elemento pela soma de dois números anteriores:
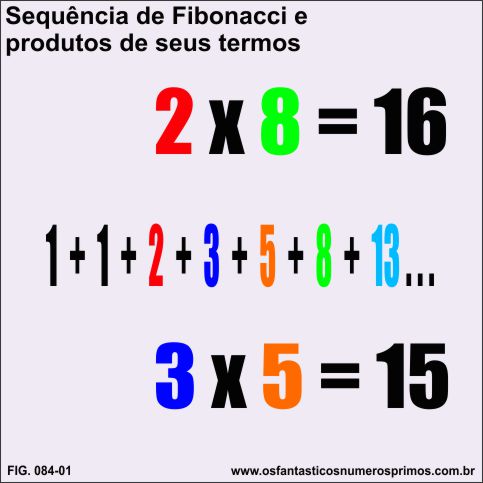
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,..
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
Neste estudo veremos que o produto dos extremos e o produto dos meios ou o produto dos meios e o produto dos extremos de números de Fibonacci apresentam como diferença também um número de Fibonacci.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,..
O produto dos extremos
2 x 8 = 16
O produto dos meios
3 x 5 = 15
A diferença entre os produtos
16 - 15 =1
1 é um número de Fibonacci
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,..
Exemplo 1)
O produto dos extremos
2 x 21 = 42
O produto dos meios
3 x 13 = 39
A diferença entre os produtos
42 - 39 = 3
3 é um número de Fibonacci
Exemplo 2)
O produto dos extremos
3 x 13 = 39
O produto dos meios
5 x 8 = 40
A diferença entre os produtos
40 - 39 =1
1 é um número de Fibonacci
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,..
Exemplo 3)
O produto dos extremos
2 x 55 = 110
O produto dos meios
3 x 34 = 102
A diferença entre os produtos
110 - 102 = 8
8 é um número de Fibonacci
Exemplo 4)
O produto dos extremos
3 x 34 = 102
O produto dos meios
5 x 21 = 105
A diferença entre os produtos
105 - 102 = 3
3 é um número de Fibonacci
Exemplo 5)
O produto dos extremos
3 x 21 = 105
O produto dos meios
8 x 13 = 104
A diferença entre os produtos
105 - 104 = 1
1 é um número de Fibonacci
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,..
Exemplo 6)
O produto dos extremos
2 x 144=288
O produto dos meios
3 x 89 = 267
A diferença entre os produtos
288 - 267 = 21
21 é um número de Fibonacci
Exemplo 7)
O produto dos extremos
3 x 89 = 267
O produto dos meios
5 x 55 = 275
A diferença entre os produtos
275 - 267 =8
8 é um número de Fibonacci
Exemplo 8)
O produto dos extremos
5 x 55 = 275
O produto dos meios
8 x 34 = 272
A diferença entre os produtos
275 - 272 = 3
3 é um número de Fibonacci
Exemplo 9)
O produto dos extremos
8 x 34 = 272
O produto dos meios
13 x 21 = 273
A diferença entre os produtos
273 - 273 =1
1 é um número de Fibonacci
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181,..
Exemplo 10)
O produto dos extremos
2 x 377 = 754
O produto dos meios
3 x 233 = 699
A diferença entre os produtos
754 - 699 = 55
55 é um número de Fibonacci
Exemplo 11)
O produto dos extremos
3 x 233 = 699
O produto dos meios
5 x 144 = 720
A diferença entre os produtos
720 - 699 = 21
21 é um número de Fibonacci
Exemplo 12)
O produto dos extremos
5 x 144 = 720
O produto dos meios
8 x 89 = 712
A diferença entre os produtos
720 - 712 = 8
8 é um número de Fibonacci
Exemplo 13)
O produto dos extremos
8 x 89 = 712
O produto dos meios
13 x 55 = 715
A diferença entre os produtos
715 - 712 = 3
3 é um número de Fibonacci
Exemplo 14)
O produto dos extremos
13 x 55 = 715
O produto dos meios
21 x 34 = 714
A diferença entre os produtos
715 - 714 =1
1 é um número de Fibonacci
Sequência de Fibonacci
A tabela demonstra os primeiros 54 números da Sequência de Fibonacci.
Sequência de Fibonacci Posição Números de Fibonacci 1 1 2 1 3 2 4 3 5 5 6 8 7 13 8 21 9 34 10 55 11 89 12 144 13 233 14 377 15 610 16 987 17 1.597 18 2.584 19 4.181 20 6.765 21 10.946 22 17.711 23 28.657 24 46.368 25 75.025 26 121.393 27 196.418 28 317.811 29 514.229 30 832.040 31 1.346.269 32 2.178.309 33 3.524.578 34 5.702.887 35 9.227.465 36 14.930.352 37 24.157.817 38 39.088.169 39 63.245.986 40 102.334.155 41 165.580.141 42 267.914.296 43 433.494.437 44 701.408.733 45 1.134.903.170 46 1836311903 47 2.971.215.073 48 4.807.526.976 49 7.778.742.049 50 12.586.269.025 51 20.365.011.074 52 32.951.280.099 53 53.316.291.173 54 86.267.571.272 www.osfantasticosnumerosprimos.com.br
Autor: Ricardo Silva
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato