capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo

Página de estudos de matemática e sequências numéricas

Sequências de Fibonacci semelhantes e números primos- 255

Assim como o Teorema de Pitágoras possui aplicações em várias áreas das ciências como Matemática, Física, Química, Biologia, etc. e diversas demostrações geométricas; a Sequência de Fibonacci não foge à regra, além de suas propriedades numéricas e algébricas, é uma sequência que aparece na Fauna, Flora, Fenômenos Físicos, Arte, Arquitetura, Geometria, etc.

Duas importantes propriedades matemáticas foram descobertas na sequência numérica relacionada a um problema em que se desejava saber quantos coelhos, em um ano, um casal de coelhos procriaria em um viveiro, descartando condições expecionais como morte, doenças, etc.

O problema dos coelhos se encontra publicado no livro Liber Abaci (Livro de Cálculos) publicado no ano de 1202, obra de Leonardo Fibonacci, também conhecido como Leonardo Pisano, Leonardo de Pisa.

A primeira descoberta foi feita pelo astronômo, astrólogo e matemático alemão, Johannes Kepler que quanto mais se avançava a sequência numérica, o quociente de um termo por um termo anterior, tendia ao número 1,6180339887 498948 48... que mais tarde foi denominado Número phi (Ф), Número de Ouro.

A segunda descoberta, deve-se ao matemático francês, François-Édouard-Anatole Lucas (1842-1891), quem notou que a soma de dois números tinha como resultado o próximo número da sequência.

Grande estudioso das obras de Leonardo Fibonacci, François-Édouard-Anatole Lucas é quem denominou e popularizou a Sequência de Fibonacci e apartir dela devirou uma outra sequência, denominda de Sequência de Lucas.

Diversos outros matemáticos descobriram novas propriedades na Sequência de Fibonacci e inclusive há a The Fibonacci Association, entidade estadunidense que realiza estudos, promove conferências sobre Fibonacci e suas obras.

Sequência de Fibonacci

A Sequência de Fibonacci é formada pelo seguinte método: repete-se o 1 duas vezes e a partir do terceiro elemento pela soma de dois números anteriores.

1 + 1 = 2

2 + 1 = 3

3 + 2 = 5

Número de Ouro

O quociente entre um número e seu antecedente da Sequência de Fibonacci, tende ao Número phi (Ф), Número de Ouro.

20 Primeiros Números de Fibonacci

ordem / índice	primo	número de	Número de
		Fibonacci	Ouro

F 1		1
F 2		1	2
F 3	sim	2	1,5
F 4	sim	3	1,666666667
F 5	sim	5	1,6
F 6		8	1,625
F 7	sim	13	1,615384615
F 8		21	1,619047619
F 9		34	1,617647059
F 10		55	1,618181818
F 11	sim	89	1,617977528
F 12		144	1,618055556
F 13	sim	233	1,618025751
F 14		377	1,618037135
F 15		610	1,618032787
F 16		987	1,618034448
F 17	sim	1.597	1,618033813
F 18		2.584	1,618034056
F 19		4.181	1,618033963
F 20		6.765	1,618033999

www.osfantasticosnumerosprimos.com.br

Números Primos de Fibonacci

Na coluna ordem/índice cujo número é impar há ocorrência de número primo, incluindo o único índice par F4 = 3

Esta ocorrência não é constante, conforme a ordem/índice no detalhe da tabela, os números não são primos.

F 31	13.46.269	não é primo
F 37	24.157.817	não é primo
F 41	165.580.141	não é primo

Sequência de Lucas / Número de Lucas

François-Édouard-Anatole Lucas, em seus estudos com a Sequência de Fibonacci, criou uma outra sequência, que leva o seu nome: Sequência de Lucas.

Somando-se números dois a dois (células verde), com um intervalo entre eles, da Sequência de Fibonacci e posteriormente os intervalos forma-se a Sequência de Lucas, sequência esta utilizada em Ciências da Computação, Criptografia e testes de Primalidade (para se saber se um número é primo ou não).

Sequência de Fibonacci

	1	1	2	3	5	8	13	21	34	55	89	144	233

		3		7		18		47		123		322
			4		11		29		76		199

Sequência de Lucas

2	1	3	4	7	11	18	29	47	76	123	199	322	521

Sequência de Fibonacci e Números Primos

Na Monografia, de Ricardo Alexandre da Rocha Dias, Algumas evidências computacionais da infinitude dos números primos de Fibonacci e generalizações destes, publicado no ano de 2008, o autor apresenta interessantíssimas estatísticas realizadas com 27.000 (vinte e sete mil) primeiros números de Fibonacci:

a) dos 27.000 primeiros números da Sequência de Fibonacci testados, 28 são números primos;

Total de Números de Fibonacci testados	27000

Qtde de num. primos de Fibonacci encontrados	28

Percentual	0,103%
Qtde de primos terminados em1	2

Qtde de primos terminados em3	6

Qtde de primos terminados em7	7

Qtde de primos terminados em 9	11

Tabela 6.1 - Dados da Sequência de Fibonacci

b) dos 27.000 primeiros números da Sequência de Fibonacci testados, o maior número primo possui 5.342 digitos;

c) a razão entre a ordem/índice e as quantidades de dígitos dos números primos encontrados apresentam resultado próximo de 4,8;

d) a razão entre a quantidade de dígitos de número primo de Fibonacci e um prmo anterior apresenta resultado próximo de 1,7712;

e) a razão entre uma ordem/índice com uma ordem/índice anterior apresenta resultado próximo de 1,7712;

f) nem todos os índices que são primos, exemplos: F 31, F 37, F41,.., apresentam números de Fibonacci primos (o grifo é nosso);

g) há grandes intervalos referente à ordem/índice que não ocorrem números de Fibonacci que são primos.

Estas duas últimas constatações f) e g) são objetos de estudos que serão apresentados nos topicos a seguir.


ordem	Números	razão
/ índice	de	entre
	digitos	ordem/índice

F 3	1
F 4	1
F 5	2
F 7	2	3,5
F 11	2	5,5
F 13	3	4,33
F 17	4	4,25
F 23	5	4,6
F 29	6	4,83

F 31			não é primo
F 37			não é primo
F 41			não é primo

F 43	9	4,77
F 47	10	4,7
F 83	17	4,88

			não há primos

F 131	28	4,67
F 137	29	4,72

			não há primos

F 359	76	4,72
F 431	90	4,78
F 433	91	4,75
F 449	94	4,77
F 509	107	4,75
F 569	119	4,78
F 571	119	4,79
F 2971	621	4,78
F 4723	987	4,78
F 5387	1126	4,78
F9311	1946	4,78
F 9377	2023	4,63
F 1431	3016	4,78
F 25561	5342	4,78

Tabela 6.2 – Índices dos primos de Fibonacci e quantidades de dígitos destes

Tabela 6.3 – índices / número de dígitos

Sequência de Fibonacci e tabuada

As propriedades numéricas e algébricas relacionadas à Sequência de Fibonacci podem aplicadas por exemplo na eleboração de tabuada.

veja matéria:

011-estudos-253-tabuada-sequencia-fibonacci

Tabuada da Sequência de Fibonacci

1	1	2	3	5	8	13	21	34	55	89	144	233	377	610...

2	2	4	6	10	16	26	42	68	110	178	288	466	754	1220

3	3	6	9	15	24	39	63	102	165	267	432	699	1131	1830

4	4	8	12	20	32	52	84	136	220	356	566	1278	1844	3122

5	5	10	15	25	40	65	105	170	275	445	720	1165	1885	3050

6	6	12	18	30	48	78	126	204	330	534	864	1398	2262	3660

7	7	14	21	35	56	91	147	238	385	623	1008	1631	2639	42270

8	8	16	24	40	64	104	168	272	440	712	1152	1864	3016	4880

9	9	18	27	45	72	117	189	306	495	801	1296	2097	3393	5490

www.osfantasticosnumerosprimos.com.br

Sequência de Fibonacci semelhantes

A partir de dois números consecutivos também são possíveis de se formarem diversas outras sequências numéricas com as propriedades numéricas e algébricas relacionadas à Sequência de Fibonacci.

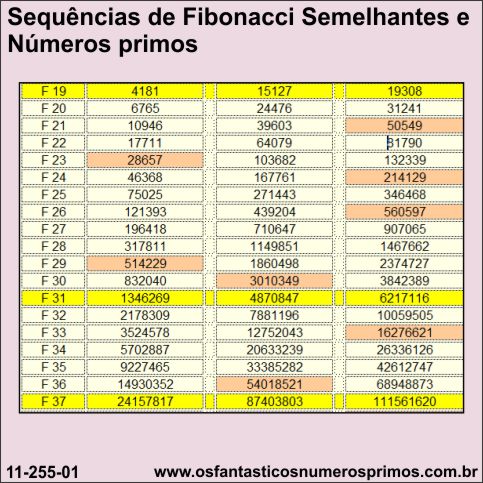
Na tabela Sequências de Fibonacci Semelhantes são apresentadas algumas sequências numéricas em que se podem verificar as seguintes propriedades:

a) as diferenças entre termos correspondentes tem como resultado a Sequência de Fibonacci (linhas amarela);

b) a razão entre um termo e seu antecedente de cada sequência tende ao número de ouro.

Exemplos:

843 : 521 = 1,6180 4222 6487 5239 9232 2456 8138 196

1076 : 665 = 1,6180 4511 2781 9548 8721 8045 1127 82

1309 : 809 = 1,6180 46971 5698 3930 7787 3918 4178

Sequência de Fibonacci

1	1	2	3	5	8	13	21	34	55	89	144	233

Sequências de Fibonacci Semelhantes

3	4	7	11	18	29	47	76	123	199	322	521	843

1	1	2	3	5	8	13	21	34	55	89	144	233

4	5	9	14	23	37	60	97	157	254	411	665	1076

1	1	2	3	5	8	13	21	34	55	89	144	233

5	6	11	17	28	45	73	118	191	309	500	809	1309

1	1	2	3	5	8	13	21	34	55	89	144	233

6	7	13	20	33	53	86	139	225	364	589	953	1542

1	1	2	3	5	8	13	21	34	55	89	144	233

7	8	15	23	38	61	99	160	259	419	678	1097	1775

1	1	2	3	5	8	13	21	34	55	89	144	233

8	9	17	26	43	69	112	181	293	474	767	1241	2008

1	1	2	3	5	8	13	21	34	55	89	144	233

9	10	19	29	48	77	125	202	327	529	856	1385	2241

1	1	2	3	5	8	13	21	34	55	89	144	233

10	11	21	32	53	85	138	223	361	584	945	1529	2474

www.osfantasticosnumerosprimos.com.br

c) as sequências numéricas geradas receberam identificações a partir dos dois primeiros números consecutivos que as formam: Sequência 3-4, 4-5, 5-6, 7-8, 8-9, 9-10,...;

d) nas sequências numéricas geradas, os números primos recaem em ordem/índice pares com maior frequência;

e) nas ordem/índice (F19, F31, F37, F41) - linhas amarela - que não ocorrem números primos na Sequência de Fibonacci, nas sequências numéricas geradas também não ocorrem primos.

f) nas ordem/índice (F19, F31, F37, F41) de sequências numéricas geradas cuja a identificação começa em impar (3-4, 5-6, 7-8, 9-10,...), as terminações dos números seguem o seguinte padrão: impar, ímpar, ímpar, par;

g) nas ordem/índice (F19, F31, F37, F41) de sequências numéricas geradas cuja a identificação começa em par (4-5, 6-7, 8-9, 10-11,...), as terminações dos números seguem o seguinte padrão: par, par, par, ímpar;

Todas estas constatações foram realizadas em 12 sequências numéricas com 50 números cada uma e comparadas com a Sequência de Fibonacci por meio da planilha digital Excel que tem limitação de 15 dígitos para números nas células, portanto não foi possível prosseguir os testes.

Prezado visitante, professor, profissional de exatas, estudante de matemática, se você tem interesse em dar continuidade a este estudo, por gentileza, entre em contato, pois para se fazer testes mais elaborados são necessários potentes computadores e específicos programas aplicativos.

Sequências de Fibonacci Semelhantes

ordem/	Sequência	Sequência	Sequência
índice	de Fibonacci	3-4	4-5

F 1	1	3	4
F 2	1	4	5
F 3	2	7	9
F 4	3	11	14
F 5	5	18	23
F 6	8	29	37
F 7	13	47	60
F 8	21	76	97
F 9	34	123	157
F 10	55	199	254
F 11	89	322	411
F 12	144	521	665
F 13	233	843	1076
F 14	377	1364	1741
F 15	610	2207	2817
F 16	987	3571	4558
F 17	1597	5778	7375
F 18	2584	9349	11933
F 19	4181	15127	19308
F 20	6765	24476	31241
F 21	10946	39603	50549
F 22	17711	64079	81790
F 23	28657	103682	132339
F 24	46368	167761	214129
F 25	75025	271443	346468
F 26	121393	439204	560597
F 27	196418	710647	907065
F 28	317811	1149851	1467662
F 29	514229	1860498	2374727
F 30	832040	3010349	3842389
F 31	1346269	4870847	6217116
F 32	2178309	7881196	10059505
F 33	3524578	12752043	16276621
F 34	5702887	20633239	26336126
F 35	9227465	33385282	42612747
F 36	14930352	54018521	68948873
F 37	24157817	87403803	111561620
F 38	39088169	141422324	180510493
F 39	63245986	228826127	292072113
F 40	102334155	370248451	472582606
F 41	165580141	599074578	764654719
F 42	267914296	969323029	1237237325
F 43	433494437	1568397607	2001892044
F 44	701408733	2537720636	3239129369
F 45	1134903170	4106118243	5241021413
F 46	1836311903	6643838879	8480150782
F 47	2971215073	10749957122	13721172195
F 48	4807526976	17393796001	22201322977
F 49	7778742049	28143753123	35922495172
F 50	12586269025	45537549124	58123818149

www.osfantasticosnumerosprimos.com.br

Observação importante:

Para a verificação e confirmação de números primos das Sequências de Fibonacci Semelhantes, utilizou-se o WebSite Império do Números.

Autor: Ricardo Silva - maio /2020

Fontes Bibliográficas:

CARVALHO, Maria Cecília Costa e Silva. Padrões Numéricos e Sequências - São Paulo: Moderna, 1997

DIAS , Ricardo Alexandre da Rocha. Algumas evidências computacionais da infinitude dos números primos de Fibonacci e generalizações destes. Universidade Federal do Rio Grande do Norte Centro de Ciências Exatas e da Terra Departamento de Informática e Matemática Aplicada Curso de Ciências da Computação. Natal - RN, 2008.

HUNTLEY, H. E. A divina Proporção. Trad. de Luiz Carlos Ascêncio Nunes. Brasília. Universidade de Brasília., 1985.

Império dos números

The Fibonacci Association