logotipo os fantasticos numeros primos
capa dos livros: os fantásticos números primos, sequências numéricas mágicas, estudos de sequências númericas, o triângulo retângulo
Página de estudos de matemática e sequências numéricas

Números de Fermat 4x + 1 e o Triângulo Numérico 15 - 599

Números de Fermat da forma 4x + 1 são números que podem ser escritos como soma de 2 quadrados.

Número primo da forma 4x + 1 tem uma única dupla de soma de 2 quadrados enquanto números compostos têm mais de 1 dupla de soma de 2 quadrados.

Números de Fermat da forma 4x + 3 não podem ser escritos como soma de 2 quadrados.

Números de Fermat 4x + 1 e o Triângulo Numérico 15

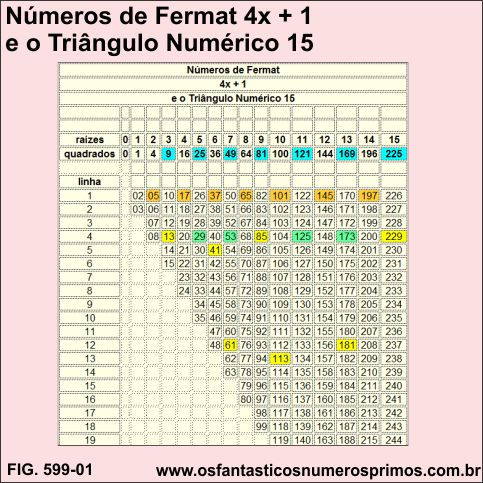
O presente estudo demonstra o Triângulo Numérico 15, um dispositivo numérico no qual números das formas 4x + 1 e 4x + 3 apresentam estreitas relações com sequências numéricas famosas, tais como: números triangulares, números retangulares, números quadrados perfeitos, números primos, números primos gêmeos, bem como, interessantes padrões geométricos com termos de sequências numéricas famosas.

Triângulo Numérico 15 - características construtivas

O Triângulo Numérico 15 possue as seguintes características construtivas:

a) o ângulo reto (90 graus) se encontra à direira superior;

b) linha das raízes quadradas;

c) linha dos números quadrados perfeitos (azul);

d) as colunas são formadas por progressões aritméticas a partir de cada número quadrado perfeito, somando-se sempre 1 unidade, isto é, razão 1 e terminando em um número antessor a um quadrado perfeito.

Números de Fermat
4x + 1 e 4x + 3
e o Triângulo Numérico 15
                                 
                                 
raízes 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
quadrados 0 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225
                             
linha                              
1 02 05 10 17 26 37 50 65 82 101 122 145 170 197 226
2 03 06 11 18 27 38 51 66 83 102 123 146 171 198 227
3 07 12 19 28 39 52 67 84 103 124 147 172 199 228
4 08 13 20 29 40 53 68 85 104 125 148 173 200 229
5 14 21 30 41 54 69 86 105 126 149 174 201 230
6 15 22 31 42 55 70 87 106 127 150 175 202 231
7 23 32 43 56 71 88 107 128 151 176 203 232
8 24 33 44 57 72 89 108 129 152 177 204 233
9 34 45 58 73 90 109 130 153 178 205 234
10 35 46 59 74 91 110 131 154 179 206 235
11 47 60 75 92 111 132 155 180 207 236
12 48 61 76 93 112 133 156 181 208 237
13 62 77 94 113 134 157 182 209 238
14 63 78 95 114 135 158 183 210 239
15 79 96 115 136 159 184 211 240
16 80 97 116 137 160 185 212 241
17 98 117 138 161 186 213 242
18 99 118 139 162 187 214 243
19 119 140 163 188 215 244
20 120 141 164 189 216 245
21 142 165 190 217 246
22 143 166 191 218 247
23 167 192 219 248
24 168 193 220 249
25 194 221 250
26 195 222 251
27 223 252
28 224 253
29 254
30 255
 
www.osfantasticosnumerosprimos.com.br

Fonte: triângulo adaptado de : Marques, David Dias. O Triângulo Numérico 15 e a Espiral de Ulam. em david-dias-marques-2025-009 -o-triangulo-numerico-15-e-a-espiral-de-ulam

Triângulo Numérico 15 - propriedades numéricas (4x+1)

a) quadrados perfeitos ímpares (azul) são da forma 4x + 1, onde x é um número retangular;

4 x 2 + 1 = 9

4 x 6 + 1 = 25

4 x 12 + 1 = 49

Os números quadrados perfeitos aparecem alinhados horizontalmente no Triângulo Numérico 15.

b) 4 multiplicado por quadrado par somado 1 unidade é da forma 4x + 1 (laranja), onde x é um número quadrado perfeito;

4 x 1 + 1 = 9

4 x 4 + 1 = 17

4 x 9 + 1 = 37

Os números 5, 17, 37, 65, 101, 145,... aparecem alinhados horizontalmente no Triângulo Numérico 15.

c) 4 multiplicado por número triangular somado 1 unidade é da forma 4x + 1 (amarelo), onde x é um número triangular;

4 x 1 + 1 = 5

4 x 3 + 1 = 13

4 x 6 + 1 = 25

d) 4 multiplicado por determinado número primo somado 1 unidade é da forma 4x + 1 (verde);

4 x 7 = 28 + 1 = 29 (primo)

4 x 43 = 172 + 1 = 173 (primo)

4 x 67 = 268 + 1 = 269 (primo)

4 x 79 = 316 + 1 = 317 (primo)

4 x 127 = 508 + 1 = 509 (primo)

Interessante destacar que: 7, 43, 67, 79, 127 são números da forma 4x + 3.

Triângulo Numérico 15 - propriedades numéricas (4x+3)

a) números da forma 4x + 3 são números que não podem ser escritos como soma de 2 quadrados e aparecem alinhados em duplas de linhas paralelas e em movimentos "zigue-zague";

b) interessante observar que a soma de cada 2 ordens de linhas, são números da forma 4x + 1.

2 + 3 = 5 ( 5 é da forma 4x + 1 )

6 + 7 = 13 ( 13 é da forma 4x + 1)

10 + 11 = 21 ( 21 é da forma 4x + 1)

Números de Fermat
4x + 1 e 4x + 3
e o Triângulo Numérico 15
                                 
raízes 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
quadrados 0 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225
                             
linha                              
1 02 05 10 17 26 37 50 65 82 101 122 145 170 197 226
2 03 06 11 18 27 38 51 66 83 102 123 146 171 198 227
3 07 12 19 28 39 52 67 84 103 124 147 172 199 228
4 08 13 20 29 40 53 68 85 104 125 148 173 200 229
5 14 21 30 41 54 69 86 105 126 149 174 201 230
6 15 22 31 42 55 70 87 106 127 150 175 202 231
7 23 32 43 56 71 88 107 128 151 176 203 232
8 24 33 44 57 72 89 108 129 152 177 204 233
9 34 45 58 73 90 109 130 153 178 205 234
10 35 46 59 74 91 110 131 154 179 206 235
11 47 60 75 92 111 132 155 180 207 236
12 48 61 76 93 112 133 156 181 208 237
13 62 77 94 113 134 157 182 209 238
14 63 78 95 114 135 158 183 210 239
15 79 96 115 136 159 184 211 240
16 80 97 116 137 160 185 212 241
17 98 117 138 161 186 213 242
18 99 118 139 162 187 214 243
19 119 140 163 188 215 244
20 120 141 164 189 216 245
21 142 165 190 217 246
22 143 166 191 218 247
23 167 192 219 248
24 168 193 220 249
25 194 221 250
26 195 222 251
27 223 252
28 224 253
29 254
30 255
 
www.osfantasticosnumerosprimos.com.br

Fonte: triângulo adaptado de : Marques, David Dias. O Triângulo Numérico 15 e a Espiral de Ulam. em david-dias-marques-2025-009 -o-triangulo-numerico-15-e-a-espiral-de-ulam

Triângulo Numérico 15 - Média Aritmética

a) números da forma 4x + 1 (amarelo)

b) números da forma 4x + 3 (verde)

O Triângulo Numérico 15 possue uma interessantíssima propriedade relacionada as formas 4x + 1 e 4x + 3 que as unem e que é a Média Aritmética.

A média aritmética de 2 números da forma 4x + 1 é um número da forma 4x + 3.

Exemplos:

( 13 + 17 ) / 2 = 15 é da forma 4x + 3

( 17 + 21 ) / 2 = 19 é da forma 4x + 3

( 21 + 25 ) / 2 = 23 é da forma 4x + 3

A média aritmética de 2 números da forma 4x + 3 é um número da forma 4x + 1.

Exemplos:

( 7 + 11 ) / 2 = 9 é da forma 4x + 1

( 11 + 15 ) / 2 = 13 é da forma 4x + 1

( 15 + 19 ) / 2 = 17 é da forma 4x + 1

Interessante observar que o padrão geométrico formado é semelhante a um tabuleiro de Jogo de Xadrez.

Números de Fermat
4x + 1 e 4x + 3
e o Triângulo Numérico 15
                                 
raízes 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
quadrados 0 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225
                             
linha                              
1 02 05 10 17 26 37 50 65 82 101 122 145 170 197 226
2 03 06 11 18 27 38 51 66 83 102 123 146 171 198 227
3 07 12 19 28 39 52 67 84 103 124 147 172 199 228
4 08 13 20 29 40 53 68 85 104 125 148 173 200 229
5 14 21 30 41 54 69 86 105 126 149 174 201 230
6 15 22 31 42 55 70 87 106 127 150 175 202 231
7 23 32 43 56 71 88 107 128 151 176 203 232
8 24 33 44 57 72 89 108 129 152 177 204 233
9 34 45 58 73 90 109 130 153 178 205 234
10 35 46 59 74 91 110 131 154 179 206 235
11 47 60 75 92 111 132 155 180 207 236
12 48 61 76 93 112 133 156 181 208 237
13 62 77 94 113 134 157 182 209 238
14 63 78 95 114 135 158 183 210 239
15 79 96 115 136 159 184 211 240
16 80 97 116 137 160 185 212 241
17 98 117 138 161 186 213 242
18 99 118 139 162 187 214 243
19 119 140 163 188 215 244
20 120 141 164 189 216 245
21 142 165 190 217 246
22 143 166 191 218 247
23 167 192 219 248
24 168 193 220 249
25 194 221 250
26 195 222 251
27 223 252
28 224 253
29 254
30 255
 
www.osfantasticosnumerosprimos.com.br

Fonte: triângulo adaptado de : Marques, David Dias. O Triângulo Numérico 15 e a Espiral de Ulam. em david-dias-marques-2025-009 -o-triangulo-numerico-15-e-a-espiral-de-ulam

Triângulo Numérico 15 - Bissetriz

A bissetriz a partir do ângulo superior esquerdo do Triângulo Númérico 15 é formada pela sequência dos números retangulares (cor azul).

Números Retangulares

Números retangulares são números que são produtos de 2 números consecutivos.

Números primos gêmeos são números primos que têm como diferença 2 unidades.

Interessante observar que cada número retangular é a média aritmética entre números de Fermat da forma 4x + 1 e 4x + 3 e vice versa e de forma alternada, havendo ocorrências de números primos gêmeos.

Números de Fermat
4x + 1 e 4x + 3
e o Triângulo Numérico 15
                                 
raízes 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
quadrados 0 1 4 9 16 25 36 49 64 81 100 121 144 169 196 225
                             
linha                              
1 02 05 10 17 26 37 50 65 82 101 122 145 170 197 226
2 03 06 11 18 27 38 51 66 83 102 123 146 171 198 227
3 07 12 19 28 39 52 67 84 103 124 147 172 199 228
4 08 13 20 29 40 53 68 85 104 125 148 173 200 229
5 14 21 30 41 54 69 86 105 126 149 174 201 230
6 15 22 31 42 55 70 87 106 127 150 175 202 231
7 23 32 43 56 71 88 107 128 151 176 203 232
8 24 33 44 57 72 89 108 129 152 177 204 233
9 34 45 58 73 90 109 130 153 178 205 234
10 35 46 59 74 91 110 131 154 179 206 235
11 47 60 75 92 111 132 155 180 207 236
12 48 61 76 93 112 133 156 181 208 237
13 62 77 94 113 134 157 182 209 238
14 63 78 95 114 135 158 183 210 239
15 79 96 115 136 159 184 211 240
16 80 97 116 137 160 185 212 241
17 98 117 138 161 186 213 242
18 99 118 139 162 187 214 243
19 119 140 163 188 215 244
20 120 141 164 189 216 245
21 142 165 190 217 246
22 143 166 191 218 247
23 167 192 219 248
24 168 193 220 249
25 194 221 250
26 195 222 251
27 223 252
28 224 253
29 254
30 255
 
www.osfantasticosnumerosprimos.com.br

Fonte: triângulo adaptado de : Marques, David Dias. O Triângulo Numérico 15 e a Espiral de Ulam. em david-dias-marques-2025-009 -o-triangulo-numerico-15-e-a-espiral-de-ulam

Média aritmética de 4 números retangulares

A média aritmética de 4 números retangulares, de forma alternada, há médias que deixam resto 2 e há médias que deixam resto 1 na divisão por 4

( 2 + 6 + 12 + 20 ) / 4 = 10 - deixa resto 2 por 4

( 6 + 12 + 20 + 30 ) / 4 = 17 - deixa resto 1 por 4

( 12 + 20 + 30 + 42 ) / 4 = 26 - deixa resto 2 por 4

( 20 + 30 + 42 + 56 ) / 4 = 37 - deixa resto 1 por 4

( 30 + 42 + 56 + 72 ) / 4 = 50 - deixa resto 2 por 4

( 42 + 56 + 72 + 90 ) / 4 = 65 - deixar resto 1 por

Quadrados 2x2 - 4 células

Na bissetriz do ângulo superior esquerdo do Triângulo Númérico 15 se formam também números quadrados perfeitos.

Envolvendo 4 números em forma de quadrado (sub-quadrados 2x2 - 4 células), a diagonal principal é formada por números retangulares (azul) e a diagonal secundária (amarelo / verde; verde / verde; verde/ amarelo; amarelo / amarelo) por números alternados da formas 4x + 1 e 4x + 3.

a) a soma de 2 números retangulares consecutivos e 2 números; um da forma 4x + 1 e outro da forma 4x + 3

02 05
03 06

2 e 6 - números retangulares consecutivos

5 da forma 4x + 1

3 da forma 4x + 3

2 + 6 + 3 + 5 = 16

b) a soma de 2 números retangulares consecutivos e 2 números da forma 4x + 3

06 11
07 12

6 e 12 - números retangulares consecutivos

7 e 11 da forma 4x + 3

6 + 12 + 7 + 11 = 16

c) a soma de 2 números retangulares consecutivos e 2 números; um da forma 4x + 1 e outro da forma 4x + 3

12 19
13 20

12 e 20 - números retangulares consecutivos

13 da forma 4x + 1

19 da forma 4x + 3

12 + 20 + 13 + 19 = 64

d) a soma de 2 retangulares consecutivos e 2 números um da forma 4x + 1

20 29
21 30

20 e 30 - números retangulares consecutivos

21 da forma 4x + 1

29 da forma 4x + 3

20 + 30 + 21 + 29 = 100

Antecessor e Sucessor de Número Retangular

Ondens / Posições dos 15 primeiros números triangulares.

Números Retangulares
Ordens / Posições
 
  Número
ordem/ retangular
posição          
           
1 1 x 2 = 2
2 2 x 3 = 6
3 3 x 4 = 12
4 4 x 5 = 20
5 5 x 6 = 30
6 6 x 7 = 42
7 7 x 8 = 56
8 8 x 9 = 72
9 9 x 10 = 90
10 10 x 11 = 110
11 11 x 12 = 132
12 12 x 13 = 156
13 13 x 14 = 182
14 14 x 15 = 210
15 15 x 16 = 240
           
www.osfantasticosnumerosprimos.com.br

Os quadrados numéricos que são formados a partir da bissetriz do Triângulo Numérico 15 descritos no tópico anterior apresentam outras regularidades numéricas.

a) quadrado 1

02 05
03 06

números retangular 2 - ordem / posição 1

sucessor 3

A soma de um número retangular com seu sucessor tem como resultado um número da forma 4x + 1.

antecessor 5

números retangular 6 - ordem / posição 2

A soma de um número retangular com seu antecessor tem como resultado um número da forma 4x + 3.

b) quadrado 2

06 11
07 12

números retangular 6 - ordem / posição 2

sucessor 7

A soma de um número retangular com seu sucessor tem como resultado um número da forma 4x + 1.

antecessor 11

números retangular 12 - ordem / posição 3

A soma de um número retangular com seu antecessor tem como resultado um número da forma 4x + 3.

Quadrados 4x4 - 16 células

Envolvendo 16 números em quadrados 4x4 - 16 células ao longo da bissetriz (azul), obtêm-se outras sequências numéricas.

Quadrado 1

5 10 17 26
6 11 18 27
7 12 19 28
8 13 20 29

soma da diagonal (amarela) - quadrado perfeito 64

soma de todos os números - quadrado perfeito 256

soma da 1a linha 58

soma da 2a linha 62

soma da 3a linha 66

soma da 4a linha 70

A soma de cada linha deixa resto 2 na divisão por 4

soma da 1a coluna 26

soma da 2a coluna 46

soma da 3a coluna 74

soma da 4a coluna 110

A soma de cada coluna deixa resto 2 na divisão por 4

Quadrado 2

11 18 27 38
12 19 28 39
13 20 29 40
14 21 30 41

soma da diagonal (amarela) - quadrado perfeito 100

soma de todos os números - quadrado perfeito 400

soma da 1a linha 94

soma da 2a linha 98

soma da 3a linha 102

soma da 4a linha 106

A soma de cada linha deixa resto 2 na divisão por 4

soma da 1a coluna 50

soma da 2a coluna 78

soma da 3a coluna 114

soma da 4a coluna 158

A soma de cada coluna deixa resto 2 na divisão por 4

 

Números quadrados centrados e a forma 4x + 1

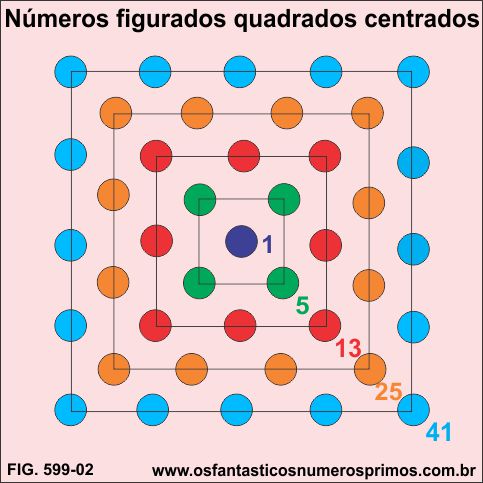
Números Figurados Quadrados Centrados são números da da forma 4x + 1.

Números quadrados centrados e a forma 4x + 1

 

Autor: Ricardo Silva - setembro/2025

Fontes Bibliográficas:

SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023

SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019

SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012

SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020

SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022

SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021

SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018

SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013

SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017

SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Matérias relacionadas:

david-dias-marques-2025-009 -o-triangulo-numerico-15-e-a-espiral-de-ulam
011-estudos-321-numeros-figurados-quadrados-centrados-sequencias-numericas
011-estudos-584-numero-primo-como-soma-de-dois-numeros-quadrados-perfeitos
011-estudos-585-numeros-primos-subtracoes-sucessivas-numeros-quadrados-perfeitos
011-estudos-590-algoritmo-da-soma-de-dois-numeros-quadrados-perfeitos
011-estudos-591-soma-de-dois-numeros-quadrados-perfeitos-e-algoritmo-s2q-2
Livro digital (e-book)
Escada de Theon
e Sequências Numéricas
Escada de Theon e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Primos e o
Método Números Atraentes
livro Números Primos e o Método Números Atraentes

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Progressões Aritméticas e Geométricas
livro digital Progressões Aritméticas e Geometricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Tabuada de Pythagoras
e Sequências Numéricas
livro digital Tabuada de Pythagoras e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Estudos de Sequências Numéricas
livro estudos de sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Os Fantásticos Números Primos
livro os fantasticos números primos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (e-book)
Ternos Pitagóricos e Sequências Numéricas
livro Ternos Pitagóricos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Senhores Professores de Matemática,

Profissionais de Exatas e

Entusiastas Matemáticos

Recebam GRATUITAMENTE
o E-book
Triângulo Retângulo

 

livro Triângulo Retângulo

FAÇA A SUA SOLICITAÇÃO

AGORA MESMO ATRAVÉS

DO E-MAIL:

contato@osfantasticos numerosprimos.com.br

Livro Digital (e-book) Descobrindo Números Primos a partir de Números Compostos
livro descobrindo numeros primos a partir numeros compostos

Mais informações, acesse:

SEÇÃO LIVROS

Livro Digital (E-book) Quadrados Mágicos e Sequências Numéricas
livro quadrados mágicos e sequências numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Triangulares e Sequências Numéricas
livro triangulares e sequências numéricas mágicas

Mais informações, acesse:

SEÇÃO LIVROS

Manual digital (E-book) Quadrado Mágico Triplo
livro quadrado mágico triplo
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Livro digital (e-book)
Números Perfeitos e Sequências Numéricas
livro Números Perfeitos e Sequências Numéricas

Mais informações, acesse:

SEÇÃO LIVROS

Manual Digital (E-book) Multiplicação através da soma de múltiplos
livro multiplicação através da soma de múltiplos
LIVRO GRATUITO

Mais informações, acesse:

SEÇÃO LIVROS

Prezado visitante, o conteúdo do

WebSite Os Fantásticos Números Primos

está protegido por direitos autorais.

O uso acadêmico e escolar está liberado,

desde que informando ao autor o local e

o meio em que será utilizado e divulgado,

através do e-mail:

contato@osfantasticosnumerosprimos.com.br

O uso comercial é proibido.

curta fantasticos numeros primos no facebook
anúncio dominó tri-minox anúncio dominó quadriminox
logotipo Ric Desing

Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.

Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).

Desenvolvimento de WebSite.

Contato

ric@osfantasticosnumerosprimos.com.br

fapage dos fantasticos numeros primos
Canal youtube dos fantasticos numeros primos