


O triângulo retângulo é uma figura geométrica ímpar e extraordinária, mesmo sendo uma figura geométrica irregular, isto é, as medidas de seus lados sendo uma diferente da outra, não apresentado simetria, etc., possue diversas propriedades numéricas, métricas, geométricas e trigonométricas.
Podemos gerar as medidas dos lados de um triângulo retângulo, com números inteiros, simplesmente escolhendo um número igual ou maior que 3, como também, um número quadrado igual ou mair que 9, números estes, sequências de 3 números inteiros, denominados de Ternos Pitagóricos Primitivos.
Para mais informações, veja abaixo, Matérias Relacionadas.
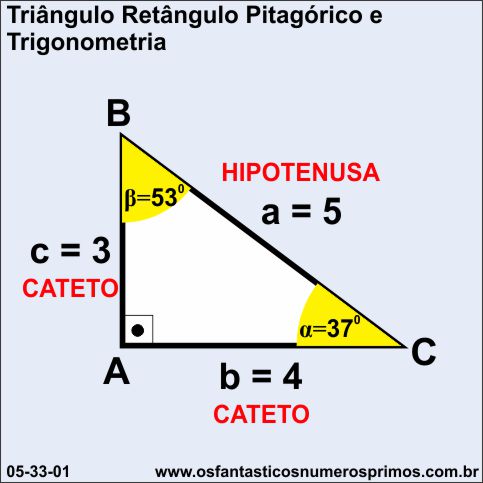
O presente estudo discorre de relações trigonométricas tendo como base o Triângulo Retângulo Pitagórico 3-4-5.
a) A divisão (razão) da medida do cateto oposto com a medida da hipotenusa tem como quociente o seno de α (sen α) de um ângulo.
| medida do cateto oposto (3) | ||
| sen α | = | _____________________ |
| medida da hipotenusa (5) |
b) A divisão (razão) da medida do cateto adjacente com a medida da hipotenusa tem como quociente o cosseno de α(cos α) de um ângulo.
| medida do cateto adjacente (4) | ||
| cos α | = | ________________________ |
| medida da hipotenusa (5) |
c) A divisão (razão) da medida do cateto oposto com a medida do cateto adjacente tem como quociente a tangente de α (tg α) de um ângulo.
| medida do cateto oposto (3) | ||
| tg α | = | ________________________ |
| medida do cateto adjacente (4) |
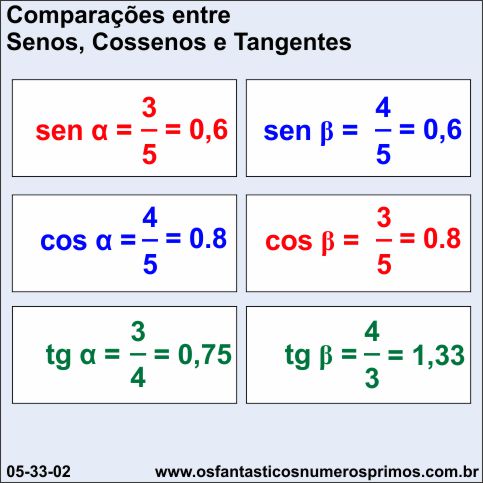
A tabela a seguir apresenta as comparações entre senos, cossenos e tangentes:
a) sen α = cos β;
b) cos α = seno β;
c) tg α e tg β são números inversos.
1) A hipotenusa do Triângulo Retângulo Pitagórico 3-4-5 mede 5cm, quanto medem os catetos?
| medida do cateto oposto | ||
| sen α | = | ______________________ |
| medida hipotenusa |
sen α = 0,6 = 6 / 10
i)
| 6 | c | |
| __ | = | ___ |
| 10 | 5 |
ii)
| 5 . 6 | ||
| c | = | ___ |
| 10 |
iii)
| 30 | ||
| c | = | ___ |
| 10 |
iv)
| c | = | 3 |
Resposta: O cateto oposto (cateto menor) mede 3cm.
| medida do cateto adjacente | ||
| cos α | = | _______________________ |
| medida da hipotenusa |
cos α = 0,8 = 8 / 10
i)
| 8 | b | |
| __ | = | ___ |
| 10 | 5 |
ii)
| 5 . 8 | ||
| b | = | ___ |
| 10 |
iii)
| 40 | ||
| b | = | ___ |
| 10 |
iv)
| b | = | 4 |
Resposta: O cateto adjacente (cateto maior) mede 4cm.
2) No Triângulo Retângulo Pitagórico 3-4-5 , o cateto oposto (cateto menor) mede 3cm e o cateto adjacente (cateto maior) mede 4cm, quanto mede a hipotenusa?
| medida do cateto oposto | ||
| sen α | = | ______________________ |
| medida da hipotenusa |
sen α = 0,6 = 6 / 10
i)
| 6 | 3 | |
| __ | = | ___ |
| 10 | a |
ii)
| 3 . 10 | ||
| a | = | ___ |
| 6 |
iii)
| 30 | ||
| a | = | ___ |
| 6 |
iv)
| a | = | 5 |
Resposta: A hipotenusa mede 5cm.
| medida do cateto adjacente | ||
| cos α | = | ______________________ |
| medida da hipotenusa |
cos α = 0,8 = 8 / 10
i)
| 8 | 4 | |
| __ | = | ___ |
| 10 | a |
ii)
| 4 . 10 | ||
| a | = | ___ |
| 8 |
iii)
| 40 | ||
| a | = | ___ |
| 8 |
iv)
| a | = | 5 |
Resposta: A hipotenusa mede 5cm.
Conhecendo o seno, o cosseno ou a tangente de um ângulo agudo, podemos saber o seno, o cosseno e a tangente desse ângulo e também seu complemento por meio das 3 propriedades representadas pelas fórmulas algébricas na figura a seguir.
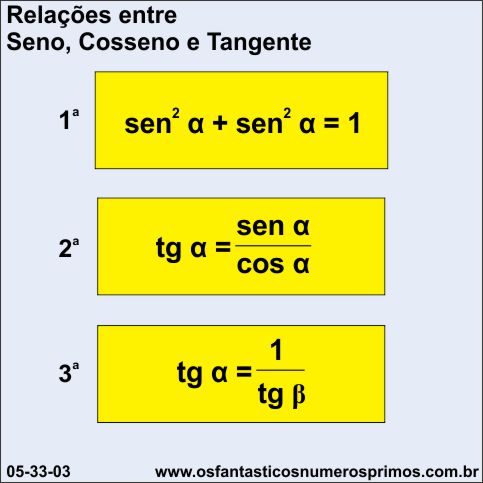
1) A hipotenusa de um Triângulo Retângulo Pitagórico mede 10cm, quanto mede seus os catetos (x) e (y), sabendo que sen α = 4 / 5?
Neste exemplo está se utilizando as medidas de um triângulo retângulo pitagórico de lados 6-8-10, derivado do Terno Pitagórico 3-4-5 cujas razões trigonométricas são contantes para toda a família de ternos pitagóricos derivados do Terno Pitagórico 3-4-5.
Outro fato a se destacar, é que o terno 3-4-5 são formados por números inteiros e primos entre si e quando formados frações, as mesmas são frações irredutíveis.
| medida do cateto oposto | ||
| sen α | = | ______________________ |
| medida da hipotenusa |
sen α = 4 / 5
i)
| 4 | x | |
| __ | = | ___ |
| 5 | 10 |
ii)
| 4 . 10 | ||
| x | = | ___ |
| 5 |
iii)
| 40 | ||
| x | = | ___ |
| 5 |
iv)
| x | = | 8 |
Resposta: O cateto (x) mede 8cm.
Continuando por meio do Teorema de Pitágoras...
10² = x² + y²
10² = 8² + y²
100 = 64 + y ²
100 - 64 = y²
36 = y²
y² = 36
y = √36
y = 6
Resposta: O cateto (y) mede 6cm.
Aplicando as relações da 1a Propriedade...
| sen²α | + | cos² α = 1 | = | 1 |
i)
| 4² | ||||
| ___ | + | cos² α | = | 1 |
| 5² |
ii)
| 4² | ||||
| cos² α | = | 1 | - | ___ |
| 5² |
iii)
| 16 | ||||
| cos² α | = | 1 | - | ___ |
| 25 |
iv) efetuando o Mínimo Múltiplo Comum
| 25 | 16 | |||
| cos² α | = | ___ | - | ___ |
| 25 | 25 |
v)
| 9 | ||
| cos² α | = | ___ |
| 25 |
vi) extraindo-se a raiz quadrada
| √9 | ||
| cos α | = | ___ |
| √25 |
vii)
| 3 | ||
| cos α | = | ___ |
| 5 |
Continuando...
| medida do cateto adjacente | ||
| cos α | = | ______________________ |
| medida da hipotenusa |
i)
| 3 | x | |
| __ | = | ___ |
| 5 | 10 |
ii)
| 3 . 10 | ||
| y | = | ___ |
| 5 |
iii)
| 30 | ||
| y | = | ___ |
| 5 |
iv)
| y | = | 6 |
Resposta: A medida do cateto (x) é 6cm.
Continuando por meio do Teorema de Pitágoras...
10² = x² + y²
10² = x² + 6²
100 = x² + 36
100 - 36 = x²
64 = x²
x² = 64
x = √64
x = 8
Resposta: O cateto (x) mede 8cm.
2) Calcule tangente do Triângulo Retângulo Pitagórico 3-4-5, sabendo que:
sen α = 0,6 = 6 / 10
cos α = 0,8 = 5 / 10
Aplicando as relações da 2a Propriedade...
| sen α | ||
| tg α | = | ____ |
| cos α |
i)
| 6 | ||
| ___ | ||
| 10 | ||
| tg α | = | _________ |
| 8 | ||
| ____ | ||
| 10 |
ii)
| 6 | 10 | |||
| tg α | = | ___ | . | ___ |
| 10 | 8 |
iii)
| 60 | ||
| tg α | = | ___ |
| 80 |
iv) convertendo o número decimal...
| tg α | = | 0,75 |
v)...em fração
| 75 | ||
| tg α | = | ___ |
| 100 |
vi) simplificando a fração...
| 75 | : 25 | 3 | |
| ___ | = | ___ | |
| 100 | : 25 | 4 |
Resposta: O numerador (cateto oposto (cateto menor) mede 3cm e o denominador (cateto adjacente (cateto maior) mede 4cm.
Na figura 05-33-02, acima, - Comparações entre Senos, Cossenos e Tangentes são apresentados os respectivos valores (razões) dos senos, cossenos e tangentes que se referem aos ângulos agudos do Triângulo Retângulo Pitagórico 3-4-5.
A partir destas razôes e consultando uma Tabela das Razões Trigonométricas, podemos saber que razão se refere a determinado ângulo, ou também, utilizando calculadoras científicas em celulares, bem como, em computadores, etc.
No exemplo do Triângulo Retângulo Pitagórico 3-4-5, em relação ao ângulo α, temos:
| razão | ângulo | |||||
| 3 | ||||||
| sen α | = | __ | = | 0,6 | = | 370 |
| 5 |
| razão | ângulo | |||||
| 4 | ||||||
| cos α | = | __ | = | 0,8 | = | 370 |
| 5 |
| razão | ângulo | |||||
| 3 | ||||||
| tg α | = | __ | = | 0,75 | = | 370 |
| 4 |
então, conclui se que:
sen 370 = 0,6
cos 370 = 0,8
tg 370 = 0,75
Querendo se saber qual é a medida do outro ângulo agudo do Triângulo Pitagórico 3-4-5, podemos prodeceder das seguintes formas:
1) Soma dos ângulos interno do triângulo
a) como a soma dos ângulos internos de um triângulo é 1800;
180 - 90 (ângulo reto) = 90
90 - 37 = 53
b) 530 é a medida do outro ângulo agudo.
Observação importante: os ângulos agudos são constantes para quaisquer triângulos pitagóricos derivados de seu respectivo terno pitagórico primitivo.
2) Comparações entre Senos, Cossenos e Tangentes
| sen 370 = 0,6 | = | cos 530 = 0,6 |
| cos 370 = 0,8 | = | sen 530 = 0,8 |
| tg 370 = 0,75 | = | tg 530 = 1,33... |
Observação: no caso das tangentes, veja que:
| 3 | ||
| __ | = | 0,75 |
| 4 |
1 / 0,75 é o inverso de 0,75
| 1 | ||
| __ | = | 1,33... |
| 0,75 |
o mesmo que...
| 4 | ||
| __ | = | 1,33... |
| 3 |
ou ainda...
| 1 | ||
| ____ | = | 0,75 |
| 1,333... |
cálculos que se referem a 3a propriedade:
| 1 | ||
| tg α | = | ____ |
| tg β |
Com a Trigonometria são possíveis de se realizarem os mais variados cálculos relacionados às medidas dos lados de triângulo retângulo com as medidas de seus ângulos e vice-versa.
Autor: Ricardo Silva - junho/2024
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Escada de Theon e Sequências Numéricas. São Paulo, edição digital, 2023
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Números Primos e o Método Número Atraentes. São Paulo, edição digital, 2022
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato