


Triângulo de Pascal ou também Triângulo Aritmético é um dispositivo numérico em que a medida que vai sendo construído, a sua estrutura vai formando sequências numéricas que possuem diversas propriedades matemáticas.
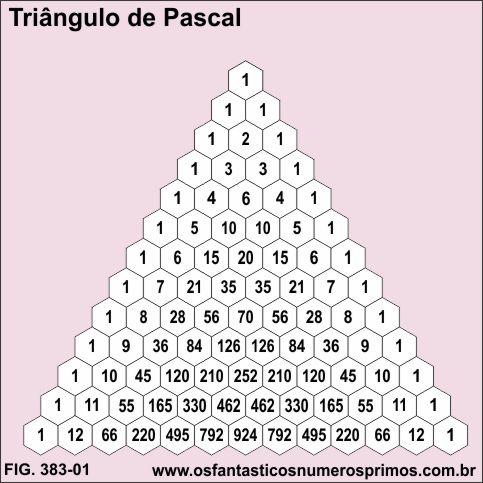
O Triângulo de Pascal possui também em sua estrutura, de forma implícita, outras sequências numéricas que podemos percebê-las quando as destacamos com figuras geométricas, por exemplo, com triângulos, hexágonos, etc.
No Triângulo de Pascal, a medida que vamos acrescentando novas linhas, vão se formando novos triângulos com bases maiores em progressão aritimética: 1, 2, 3, 4, 5, 6, ... e as somas de todos os números nas células têm como resultados números quase-perfeitos, números quase-potências de base 2 ou simplesmente Números de Mersenne.
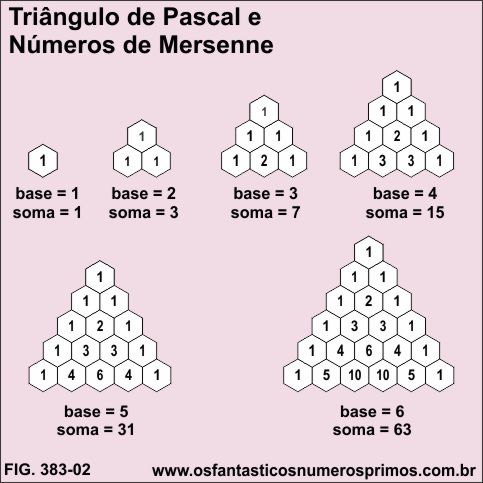
Organizando os números em uma tabela, percebe-se que determinados triângulos equiláteros cujas bases (lados) têm quantidades de células em números primos correspondem também a um Número Primo de Mersenne.
| Soma | ||||
| dos | ||||
| base | potencia | números | ||
| do | de | nos | Número | |
| triângulo | base 2 | triângulos | primo de | |
| 1 | 1 | 1 | ||
| primo | 2 | 4 | 3 | Mersenne |
| primo | 3 | 8 | 7 | Mersenne |
| 4 | 16 | 15 | ||
| primo | 5 | 32 | 31 | Mersenne |
| 6 | 64 | 63 | ||
| primo | 7 | 128 | 127 | Mersenne |
| 8 | 256 | 255 | ||
| 9 | 512 | 511 | ||
| 10 | 1024 | 1023 | ||
| 11 | 2048 | 2047 | ||
| 12 | 4096 | 4095 | ||
| primo | 13 | 8192 | 8191 | Mersenne |
| www.osfantasticosnumerosprimos.com.br | ||||
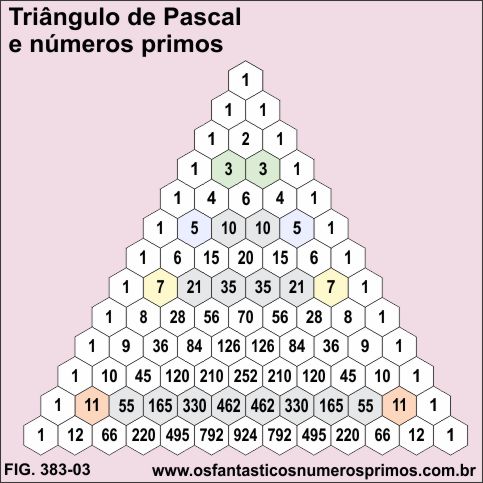
No Triângulo de Pascal, nas linhas em que os números primos "envolvem" as demais células, os números dessas células são múltiplos desse número primo:
Exemplos:
a) Linha 3 - número primo 3;
3 é múltiplo de 3.
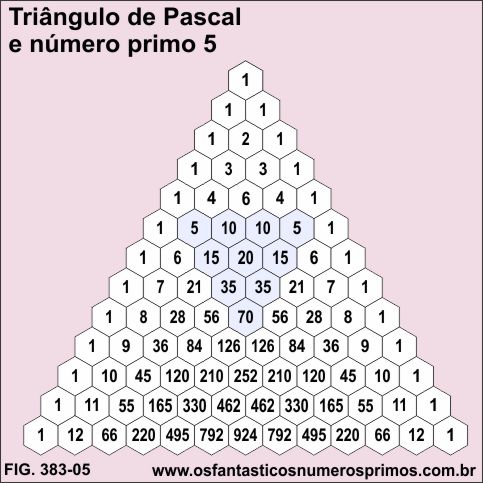
b) Linha 5 - número primo 5;
10, 10 e 5 são múltiplos de 5
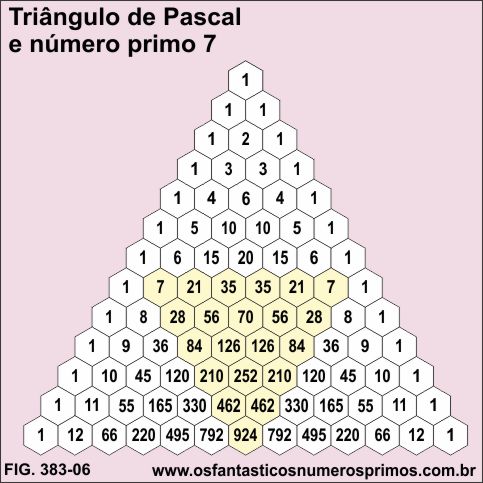
c) Linha 7 - número primo 7.
21, 35, 35 e 7 são múltiplos de 7.
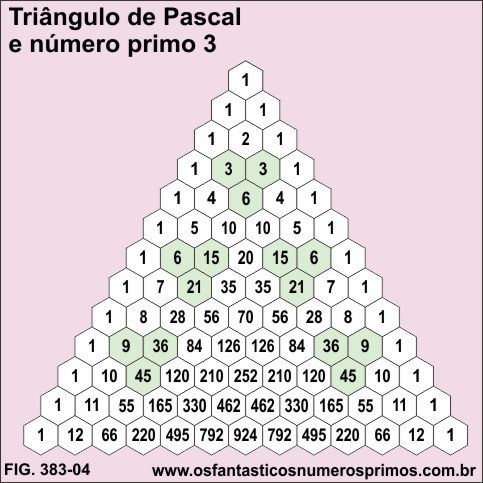
Destacando as células onde há múltiplos de 3, forma-se triângulos equiláteros de base (lado) 2 com 3 células.
Destacando as células onde há múltiplos de 5, forma-se triângulos equiláteros de base (lado) 4 com 10 células.
Destacando as células onde há múltiplos de 7, forma-se triângulos equiláteros de base (lado) 6 com 21 células.
Organizando as informações extraídas das construções dos triângulos equiláteros com múltiplos de números primos, observa-se mais padrões numéricos no Triângulo de Pascal relacionados com números triangulares:
a) os números primos e as bases são números consecutivos;
observação: a base (lado) do triângulo equilátero inscrito é 1 unidade menor que um número primo.
b) o produto de dois números consecutivos, que é um número retangular, dividido por 2, tem como resultado um número triangular;
c) a quantidade de células é múltiplo do número primo correspondente.
| Múltiplos | base (lado) | Quant. | soma |
| de | do | de | das |
| triângulo | células | células | |
| 3 | 2 | 6 | 12 |
| 5 | 4 | 10 | 220 |
| 7 | 6 | 21 | 3304 |
| www.osfantasticosnumerosprimos.com.br | |||
Autor: Ricardo Silva - maio /2022
SILVA, Ricardo José da. Descobrindo Números Primos a partir de Números Compostos. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Estudos de Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Manual do Quadrado Mágico Triplo. São Paulo, edição digital, 2019
SILVA, Ricardo José da. Os Fantásticos Números Primos. São Paulo, edição digital, 2012
SILVA, Ricardo José da. Números Perfeitos e Sequências Numéricas. São Paulo, edição digital, 2020
SILVA, Ricardo José da. Progressões Aritméticas e Geométricas - novas fórmulas de somas de PAs e PGs. São Paulo, edição digital, 2021
SILVA, Ricardo José da. Quadrados Mágicos e Sequências Numéricas. São Paulo, edição digital, 2018
SILVA, Ricardo José da. Números Triangulares e Sequências Numéricas. São Paulo, edição digital, 2013
SILVA, Ricardo José da. Ternos Pitagóricos e Sequências Numéricas. São Paulo, edição digital, 2017
SILVA, Ricardo José da. O Triângulo Retângulo - novas fórmulas algébricas e aritméticas de cálculos. São Paulo, edição digital, 2014

Mais informações, acesse:

Mais informações, acesse:
Senhores Professores de Matemática,
Profissionais de Exatas e
Entusiastas Matemáticos

FAÇA A SUA SOLICITAÇÃO
AGORA MESMO ATRAVÉS
DO E-MAIL:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:

Mais informações, acesse:
Prezado visitante, o conteúdo do
WebSite Os Fantásticos Números Primos
está protegido por direitos autorais.
O uso acadêmico e escolar está liberado,
desde que informando ao autor o local e
o meio em que será utilizado e divulgado,
através do e-mail:
contato@osfantasticosnumerosprimos.com.br
O uso comercial é proibido.




Assessoria Gráfica e de Comunicação para
Escritores Independentes
que desejam lançar obras literárias,
técnicas ou artísticas.
Projeto Gráfico, Diagramação
e Editoração Eletrônica de livros (e-books).
Desenvolvimento de WebSite.
Contato